Abstract 抽象
For modern evidence-based medicine, a well thought-out risk scoring system for predicting the occurrence of a clinical event plays an important role in selecting prevention and treatment strategies. Such an index system is often established based on the subject’s “baseline” genetic or clinical markers via a working parametric or semi-parametric model. To evaluate the adequacy of such a system, C-statistics are routinely used in the medical literature to quantify the capacity of the estimated risk score in discriminating among subjects with different event times. The C-statistic provides a global assessment of a fitted survival model for the continuous event time rather than focuses on the prediction of t-year survival for a fixed time. When the event time is possibly censored, however, the population parameters corresponding to the commonly used C-statistics may depend on the study-specific censoring distribution. In this article, we present a simple C-statistic without this shortcoming. The new procedure consistently estimates a conventional concordance measure which is free of censoring. We provide a large sample approximation to the distribution of this estimator for making inferences about the concordance measure. Results from numerical studies suggest that the new procedure performs well in finite sample.
对于现代循证医学,用于预测临床事件发生的深思熟虑的风险评分系统在选择预防和治疗策略方面起着重要作用。这样的指标系统通常是根据受试者的“基线”遗传或临床标志物通过有效的参数或半参数模型建立的。为了评估这种系统的充分性,医学文献中通常使用 C 统计量来量化估计的风险评分区分具有不同事件时间的受试者的能力。C 统计量提供对连续事件时间的拟合生存模型的全局评估,而不是侧重于对固定时间的 t 年生存率的预测。但是,当事件时间可能被删失时,与常用 C 统计量相对应的总体参数可能取决于特定于研究的删失分布。在本文中,我们提出了一个简单的 C 统计量,而没有这个缺点。新程序始终如一地估计一个没有删失的常规一致性度量。我们提供了此估计量分布的大样本近似值,用于对一致性度量进行推断。数值研究结果表明,新程序在有限样本中表现良好。
Keywords: AUC, Cox’s proportional hazards model, Framingham risk score, ROC
关键词:AUC,Cox 比例风险模型,Framingham 风险评分,ROC
1. INTRODUCTION 1. 引言
For modern clinical medicine, risk prediction procedures are valuable tools for disease prevention and management. Pioneered by the Framingham study, risk score systems have been established for assessing individual risks of developing cardiovascular diseases, cancer or many other conditions within a certain time period [1, 2, 3, 4]. A key component in the assessment of risk algorithm performance is its ability to distinguish subjects who will develop an event (“cases”) from those who will not (“controls”). This concept, known as discrimination, has been well studied and quantified for binary outcomes using measures such as the estimated area under the Receiver Operating Characteristics (ROC) curve (AUC), which is also referred to as a “C-statistic” [5]. Such a statistic is an estimated conditional probability that for any pair of “case” and “control,” the predicted risk of an event is higher for the “case” [6].
对于现代临床医学,风险预测程序是疾病预防和管理的宝贵工具。由 Framingham 研究开创,已经建立了风险评分系统,用于评估在一定时间内患心血管疾病、癌症或许多其他疾病的个体风险 [ 1, 2, 3, 4]。评估风险算法性能的一个关键组成部分是它能够区分将发生事件的受试者(“病例”)和不会发生事件的受试者(“对照”)。这个概念被称为歧视,已经使用诸如受试者工作特征 (ROC) 曲线下估计面积 (AUC) 等措施对二元结果进行了充分研究和量化,该曲线也称为“C 统计量”[ 5]。这样的统计量是一个估计的条件概率,即对于任何一对 “案例” 和 “对照” ,“案例” 的事件预测风险更高 [ 6]。
If the primary response variable is the time to a certain event, the aforementioned procedure for binary outcomes can be used to quantify the ability of the risk score system to differentiate cases from controls at a time point t. If one is not interested in a particular time point, a standard concordance measure may be used to evaluate the overall performance of the risk scoring system. Specifically, let T be the event time, Z be a p × 1 covariate vector, and g(Z) be an estimated risk score for subjects with Z. There is a large class of measures to quantify how well the risk score g(Z) predicts the distribution of T or a function thereof. A good review paper is given by Korn & Simon [7] or more recently by Hielscher et al. [8] Such prediction measures can be classified into two broad classes, one based on explicit loss functions between the risk score and the survival time and the other based on rank correlations between these two quantities. The C-statistic proposed by Harrell et al. [9, 10, 11] is essentially a rank-correlation measure, motivated by Kendall’s tau for censored survival data [12]. A critical issue for rank correlation methods is how to order survival times in the presence of censoring. Brown et al. [12] used all observations and assigned probability scores to pairs in which ordering is not obvious due to censoring, based on the pooled Kaplan-Meier estimate for T. However, the score based on the pooled Kaplan-Meier estimate may not be appropriate when the covariates are associated with T. Alternative forms of C-statistic considered in [9, 10, 11, 13] use only so-called “useable” pairs and calculate the proportion of concordant pairs among them. However, such C-statistics estimate population parameters that may depend on the current study-specific censoring distribution. In this article, we propose a modified C-statistic which is consistent for a population concordance measure that is free of censoring.
如果主要响应变量是某个事件发生的时间,则上述二元结果程序可用于量化风险评分系统在某个时间点 t 区分病例和对照的能力。如果对某个特定时间点不感兴趣,可以使用标准一致性度量来评估风险评分系统的整体性能。具体来说,设 T 为事件时间,Z 为 p × 1 协变量向量,g(Z) 为 Z 为主体的估计风险评分。有一大类度量可以量化风险评分 g(Z) 预测 T 或其函数分布的程度。Korn & Simon [ 7] 或最近的 Hielscher 等人 [ 8] 给出了一篇很好的综述论文。这种预测措施可以分为两大类,一类基于风险评分和生存时间之间的显式损失函数,另一类基于这两个量之间的等级相关性。Harrell 等人 [ 9, 10, 11] 提出的 C 统计量本质上是一种秩相关度量,由 Kendall 的 tau 驱动,用于删失生存数据 [ 12]。秩相关方法的一个关键问题是如何在存在删失的情况下对生存时间进行排序。Brown等[12]使用了所有观测值,并根据T的合并Kaplan-Meier估计,将概率分数分配给由于删失而排序不明显的对。然而,当协变量与 T 相关联时,基于合并的 Kaplan-Meier 估计的分数可能不合适。[ 9, 10, 11, 13] 中考虑的 C 统计量的替代形式仅使用所谓的“可用”对并计算它们之间一致对的比例。 然而,这种 C 统计量估计的总体参数可能取决于当前研究特定的删失分布。在本文中,我们提出了一种修改后的 C 统计量,它与没有删失的总体一致性测量是一致的。
More specifically, for two independent copies {(T1, g(Z1))′, (T2, g(Z2))′} of (T, g(Z))′, a commonly used concordance measure is
更具体地说,对于 (T, g(Z))′ 的两个独立副本 {(T 1 , g(Z 1 ))′, (T 2 , g(Z 2 ))′},常用的一致性度量是
| (1.1) |
[14]. When T is subject to right censoring, as discussed in Heagerty & Zheng [14] one would typically consider a modified Cτ with a fixed, prespecified follow-up period (0, τ), where
当T受到右删失时,如Heagerty和Zheng [14]中所讨论的那样,人们通常会考虑 τ 具有固定的、预先指定的随访期(0, τ)的修改C,其中
| (1.2) |
Estimation of (1.1) or (1.2) when the event time may be censored, however, is not straightforward [11, 13, 15]. The estimator for C or Cτ proposed by Heagerty & Zheng [14] is derived under a proportional hazards model. If this semi-parametric working model is not correctly specified, the resulting estimator may be biased. A popular nonparametric C-statistic for estimating C or Cτ was proposed by Harrell et al. [9, 10, 11] and extensively studied by Pencina & D’Agostino [13]. Note that this generalization is a weighted area under an “incident/dynamic” ROC curve [14, 16] with weights depending on the study-specific censoring distribution.
然而,当事件时间可以被删失时,估计 ( 1.1) 或 ( 1.2) 并不简单 [ 11, 13, 15]。Heagerty和Zheng [14]提出的C或C τ 的估计量是在比例风险模型下推导出来的。如果未正确指定此半参数工作模型,则生成的估计量可能会有偏差。Harrell等人提出了一种流行的非参数C统计量来估计C或C τ [ 9, 10, 11] 并被Pencina & D'Agostino [ 13]广泛研究。请注意,这种泛化是“事件/动态”ROC 曲线 [ 14, 16] 下的加权区域,其权重取决于特定于研究的删失分布。
When the study individuals have different follow-up times, the C-statistic studied by Harrell et al. [9, 10, 11] converges to an association measure that involves the study censoring distribution. In this article, under the general random censorship assumption, we provide a simple non-parametric estimator for the concordance measure in (1.2), which is free of censoring. Furthermore, we study the large sample properties of the new estimation procedure. Our proposal is illustrated with two real examples. The performance of the new proposal under various practical settings is also examined via a simulation study. Note that Gönen & Heller [17] proposed a method for censored survival data to estimate pr(T2 > T1 ∣ g(Z1) > g(Z2)), which is also a concordance measure and has a similar form to (1.1), but we do not focus on this type of measures in this paper.
当研究个体的随访时间不同时,Harrell 等人 [ 9, 10, 11] 研究的 C 统计量会收敛到涉及研究删失分布的关联度量。在本文中,在一般的随机删失假设下,我们为 ( 1.2 中的一致性测度提供了一个简单的非参数估计器),它是无删失的。此外,我们研究了新估计程序的大样本特性。我们的提案用两个真实的例子来说明。还通过模拟研究检查了新提案在各种实际设置下的性能。请注意,Gönen & Heller [ 17] 提出了一种删失生存数据估计 pr(T 2 > T 1 ∣ g(Z 1 ) > g(Z 2 )) 的方法,这也是一种一致性测量,与( 1.1)的形式相似,但我们在本文中不关注这种类型的测量。
2. INFERENCE PROCEDURES FOR DEGREE OF ASSOCIATION BETWEEN EVENT TIMES AND ESTIMATED RISK SCORES
2. 事件时间与估计风险评分之间关联程度的推理程序
In this section, we consider a non-trivial case that at least one component of the covariate vector Z is continuous. For the survival time T, let D be the corresponding censoring variable. Assume that D is independent of T and Z. Let {(Ti, Zi, Di), i = 1, …, n} be n independent copies of {(T,Z,D)}. For the ith subject, we only observe (Xi, Zi, Δi), where Xi = min (Ti, Di), and Δi equals 1 if Xi = Ti and 0 otherwise.
在本节中,我们考虑一个非平凡的情况,即协变量向量 Z 的至少一个分量是连续的。对于生存时间 T,设 D 为相应的删失变量。假设 D 独立于 T 和 Z。设 {(T, Z, D), i = 1, ..., n} 是 {(T,Z,D)} 的 n 个独立副本。对于第 i 个主题,我们只观察到 (X, Z, Δ),其中 X = min (T, D),如果 X = T,则 Δ 等于 1,否则为 0。
Suppose that we fit the data with a working parametric or semi-parametric regression model, for example, a standard Cox proportional hazards model [18]:
假设我们使用有效的参数或半参数回归模型拟合数据,例如,标准 Cox 比例风险模型 [ 18]:
| (2.1) |
where ΛZ(·) is the cumulative hazard function for subjects with covariate vector Z, Λ0(·) is the unknown baseline cumulative hazard function and β is the unknown p × 1 parameter vector. Let the maximum partial likelihood estimator for β be denoted by β̂. Note that even when the model (2.1) is not correctly specified, under a rather mild non-separable condition that there does not exist vector ζ such that pr(T1 > T2 ∣ ζ′Z1 < ζ′Z2) = 1, β̂ converges to a constant vector, say, β0, as n → ∞. This stability property is important for deriving the new inference procedure.
其中 Λ Z (·) 是具有协变量向量 Z 的主体的累积风险函数,Λ 0 (·) 是未知的基线累积风险函数,β 是未知的 p × 1 参数向量。设 β 的最大偏似然估计量用 β̂ 表示。请注意,即使模型 ( 2.1) 没有正确指定,在不存在向量ζ的相当温和的不可分条件下,使得 pr(T 1 > T 2 ∣ ζ′Z 1 < ζ′Z 2 ) = 1, β̂ 收敛到一个常数向量,比如 β 0 ,作为 n → ∞。此稳定性属性对于派生新的推理过程非常重要。
For a pair of future patients with covariate vectors
对于一对具有协变量向量
where the probability is evaluated with respect to the data, and (
其中,根据数据评估概率,以及 (
| (2.2) |
Now, since the support of the censoring variable D is usually shorter than that of the failure time T, the tail part of the estimated survival function of T is rather unstable. Therefore, we consider a truncated version of C in (2.2), that is,
现在,由于删失变量 D 的支持通常短于失效时间 T 的支持,因此 T 的估计生存函数的尾部相当不稳定。因此,我们在 ( 2.2) 中考虑 C 的截断版本,即
| (2.3) |
where τ is a prespecified time point such that pr(D > τ) > 0.
其中 τ 是预先指定的时间点,使得 pr(D > τ) > 0。
It follows from an “inverse probability weighting” technique as employed in Cheng et al. [19] for dealing with a completely different problem in survival analysis that Cτ can be consistently, nonparametrically estimated by
它遵循 Cheng 等人 [ 19] 采用的“逆概率加权”技术,用于处理生存分析中一个完全不同的问题,即 C τ 可以由
| (2.4) |
where I(·) is the indicator function and Ĝ(·) is the Kaplan-Meier estimator for the censoring distribution G(t) = pr(D > t). Heuristically, the consistency of the above estimator follows from the fact that as n → ∞, the denominator of (2.4) divided by n2 converges to
其中 I(·) 是指示函数,Ĝ(·) 是删失分布 G(t) = pr(D > t) 的 Kaplan-Meier 估计量。从启发式的角度来看,上述估计量的一致性源于以下事实:当 n → ∞时,( 2.4) 除以 n 2 的分母收敛为
Note that E {I(D > T1){G(T1)}−1∣T1} = 1 in the above equation, where the expectation is taken with respect to D. Thus, the denominator and the numerator of (2.4) divided by n2 converge to
请注意,在上述方程中,E {I(D > T 1 ){G(T 1 )} ∣ −1 T 1 } = 1,其中期望值是相对于 D 的。因此,( 2.4) 除以 n 2 的分母和分子分别收敛到
In Appendix A, we show that
在附录 A 中,我们展示了
is asymptotically normal with mean 0. Moreover, in the Appendix, we show how to use a perturbation-resampling method to approximate the distribution of W. Specifically, we show that the asymptotic distribution of W̃ given in (A.3) is the same as that of W. The realizations of W̃ can be generated easily by simulating a large number, M, of random samples from, for instance, the unit exponential. Inferences about Cτ can then be made via the normal approximation to the distribution of Ĉτ and these realizations of W̃ . For instance, a two-sided 0.95 confidence interval for Cτ would be Ĉτ ± 1.96n−1/2σ, where σ2 is the standard sample variance or a robust version thereof based on the above M realizations of W̃.
是渐近正态的,均值为 0。此外,在附录中,我们展示了如何使用扰动重采样方法来近似 W 的分布。具体来说,我们展示了 (A.3) 中给出的 W̃ 的渐近分布与 W 的渐近分布相同。W̃ 的实现可以通过模拟大量随机样本 M 来轻松生成,例如,单位指数。然后可以通过对 Ĉ 的分布 τ 和 W̃ 的这些实现的正态近似来做出关于 C τ 的推断。例如,C τ 的双侧 0.95 置信区间将是 Ĉ τ ± 1.96n −1/2 σ,其中 σ 2 是标准样本方差或基于上述 W 的 M 实现的稳健版本。
It is important to note that the C-statistic proposed by Harrell et al. [11] is
需要注意的是,Harrell 等人 [ 11] 提出的 C 统计量是
| (2.5) |
which converges to a censoring-dependent quantity,
它收敛到一个与删失相关的量,
Pencina & D’Agostino [13] formulated an alternative form of C-statistic,
Pencina & D'Agostino [ 13] 提出了一种替代形式的C-统计量,
| (2.6) |
for various τ. The limiting value of this statistic,
对于各种 τ.此统计数据的极限值
also involves the censoring distribution.
还涉及删失分布。
When there are two competing survival regression models, say A and B, one may compare the overall predictive performances of these models based on their C-statistics. Specifically, let
当有两个竞争的生存回归模型(比如 A 和 B)时,人们可以根据它们的 C 统计量来比较这些模型的整体预测性能。具体来说,模型 A 和模型 B 分别为 let
can be approximated by a normal with mean zero. Its variance can be obtained via the above perturbation-resampling method. The details of this normal approximation are given in Appendix B. To make inference about ξ, a two-sided 0.95 confidence interval is ξ̂ ± 1.96n−1/2σ̂Wξ , where
可以用均值为零的正态近似。它的方差可以通过上述扰动重采样方法获得。附录 B 中给出了这种正态近似的详细信息。为了推断 ξ,双侧 0.95 置信区间是 ξ̂ ± 1.96n −1/2 σ̂ Wξ ,其中
3. NUMERICAL STUDIES 3. 数值研究
3.1. Examples 3.1. 示例
First, we illustrate the proposed procedures with two data sets. The first one is from the Framingham Heart Study. For this data set, there were 3087 study participants whose baseline covariate vectors Z’s were obtained at their study entry times between 1991 and 1995. Here, each Z consists of age, gender, smoking status (SMK), total cholesterol (TC), HDL cholesterol (HCD), systolic blood pressure (SBP) and use of medication for high blood pressure (TxBP). These individuals were then followed until 2006. Here, the event time T is the first time that the subject experienced any of the following cardiovascular (CV) events including coronary death, myocardial infarction, coronary insufficiency, angina pectoris, fatal and non-fatal stroke, intermittent claudication, or congestive heart failure. For this data set, there are 377 such events observed during the entire follow-up period, and 282 of which occurred in the first 10 years. The Kaplan-Meier estimates for the survival distributions of both the event time T and the censoring time D are given in Figure 1. Note that most study subjects were followed for more than ten years, but less than 13 years.
首先,我们用两个数据集来说明所提出的程序。第一个来自弗雷明汉心脏研究。对于该数据集,有 3087 名研究参与者的基线协变量向量 Z 是在 1991 年至 1995 年间的研究开始时间获得的。在这里,每个 Z 由年龄、性别、吸烟状况 (SMK)、总胆固醇 (TC)、高密度脂蛋白胆固醇 (HCD)、收缩压 (SBP) 和高血压药物使用情况 (TxBP) 组成。然后对这些个体进行跟踪直到 2006 年。在这里,事件时间 T 是受试者首次经历以下任何心血管 (CV) 事件,包括冠状动脉死亡、心肌梗塞、冠状动脉功能不全、心绞痛、致命和非致命中风、间歇性跛行或充血性心力衰竭。对于该数据集,在整个随访期间观察到 377 起此类事件,其中 282 起发生在前 10 年。图 1 给出了事件时间 T 和删失时间 D 的生存分布的 Kaplan-Meier 估计值。请注意,大多数研究对象的随访时间超过 10 年,但不到 13 年。
Figure 1. 图 1.
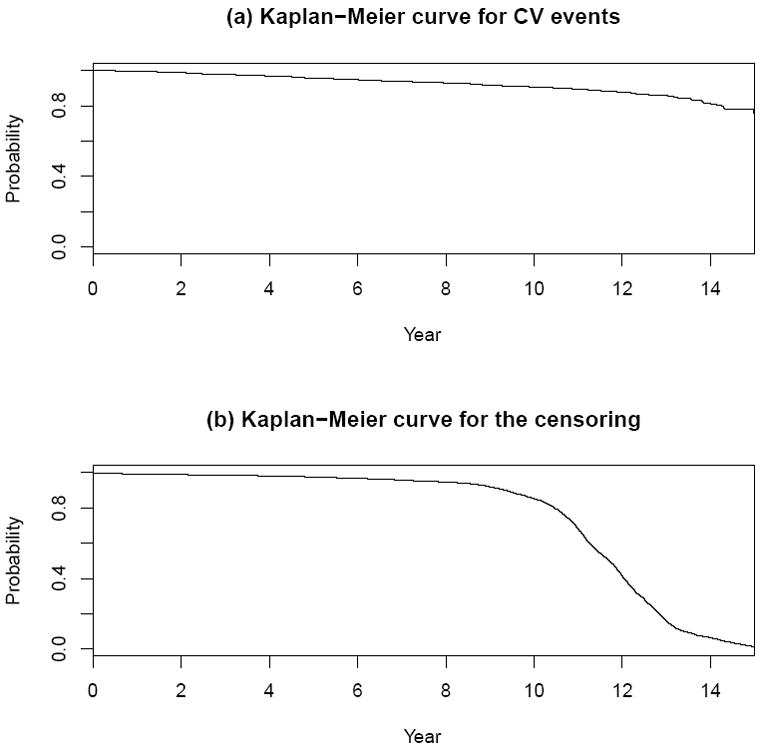
Estimates for survival functions for CV events and censoring variables with Framingham study data.
CV 事件的生存函数估计值和 Framingham 研究数据的删失变量。
We fitted the data with a Cox proportional hazards model (2.1). The resulting risk score β̂′Z0 is
我们使用 Cox 比例风险模型 ( 2.1) 拟合数据。得到的风险评分 β̂′Z 0 为
In Table 1, we present point and 0.95 interval estimates of Cτ for various τ. When τ = 8, 10, 12 (years), our results are very similar to those based on the conventional C-index (2.5) procedure with a point estimate of 0.75 and a 0.95 confidence interval of (0.73, 0.77). Note that all the τ-specific conventional C-statistics (2.6) give us similar point and interval estimates. When τ = 14, our estimated standard error for the new C-statistic is markedly larger than that of the conventional method. In this case, study subjects did not have similar follow-up times and it is known that the existing methods in the literature may not work well [13]. Note that all the results reported in Table 1 were based on M = 500 independent realizations of a random sample with n = 3087 from the unit exponential for (A.3).
在表 1 中,我们提供了各种 τ 的 C τ 的点和 0.95 区间估计值。当 τ = 8、10、12(年)时,我们的结果与基于传统 C 指数 ( 2.5) 程序的结果非常相似,点估计值为 0.75,置信区间为 (0.73, 0.77)。请注意,所有特定于 τ 的常规 C 统计量 ( 2.6) 都为我们提供了相似的点和区间估计值。当 τ = 14 时,我们对新 C 统计量的估计标准误差明显大于传统方法的标准误差。在这种情况下,研究对象没有相似的随访时间,并且已知文献中的现有方法可能效果不佳 [ 13]。请注意,表 1 中报告的所有结果均基于随机样本的 M = 500 个独立实现,其中 n = 3087 来自单位指数 (A.3)。
Table 1. 表 1.
Point estimates (Est), standard error estimates (SE) and 0.95 confidence intervals (CI) for Cτ with Framingham study data
τ C 的点估计值 (Est)、标准误差估计值 (SE) 和 0.95 置信区间 (CI) 与 Framingham 研究数据
| C-index C 指数 | New Method 新方法 | Conventional 协定的 | ||||
|---|---|---|---|---|---|---|
| τ | Est 东 | SE 她自己 | CI 那里 | Est 东 | SE 她自己 | CI 那里 |
| 8 | 0.76 | 0.02 | (0.73, 0.79) | 0.76 | 0.01 | (0.73, 0.79) |
| 10 | 0.75 | 0.01 | (0.72, 0.78) | 0.75 | 0.01 | (0.73, 0.78) |
| 12 | 0.75 | 0.01 | (0.72, 0.77) | 0.75 | 0.01 | (0.73, 0.78) |
| 14 | 0.75 | 0.02 | (0.70, 0.80) | 0.75 | 0.01 | (0.73, 0.78) |
| ∞ | NA 上 | NA 上 | NA 上 | 0.75 | 0.01 | (0.73, 0.77) |
For τ = 10 (years), we also evaluated the incremental value of HDL cholesterol by comparing the model containing all risk factors described above (Model A) with the model containing risk factors other than HDL cholesterol (Model B). Results of the Cox regression analysis were given in Table 2. The point estimate for
对于 τ = 10 (年),我们还通过将包含上述所有风险因素的模型(模型 A)与包含除 HDL 胆固醇以外的风险因素的模型(模型 B)进行比较来评估 HDL 胆固醇的增量值。表 2 给出了 Cox 回归分析的结果。的
Table 2. 表 2.
Estimates of regression parameters for Cox’s models with Framingham study data
使用 Framingham 研究数据的 Cox 模型的回归参数估计值
| Model A (with HDL) A 型(带 HDL) |
Model B (without HDL) B 型(无 HDL) |
|||||
|---|---|---|---|---|---|---|
| Est.(1) 东。 (1) | SE(2) 她自己 (2) | p(3) | Est. 东。 | SE 她自己 | p | |
| AGE/10 [yrs] 年龄/10 [岁] | 0.54 | 0.07 | 0.00 | 0.53 | 0.07 | 0.00 |
| Gender=Male 性别 = 男 | -0.41 | 0.12 | 0.00 | -0.63 | 0.11 | 0.00 |
| SMK=Yes SMK = 是 | 0.53 | 0.13 | 0.00 | 0.57 | 0.12 | 0.00 |
| TC/102[mg/dL] TC/10 2 [毫克/分升] | 0.40 | 0.15 | 0.01 | 0.34 | 0.15 | 0.03 |
| SBP/10[mmHg] 收缩压/10[mmHg] | 0.15 | 0.03 | 0.00 | 0.16 | 0.03 | 0.00 |
| IxBP=Yes IxBP=是 | 0.33 | 0.12 | 0.01 | 0.40 | 0.12 | 0.00 |
| HDL/10 [mg/dL] 高密度脂蛋白/10 [mg/dL] | -0.21 | 0.04 | 0.00 | - | - | - |
| C-index with τ = 10 (0.95 confidence interval) τ = 10 的 C 指数(0.95 置信区间) |
||||||
| Conventional 协定的 | 0.75 (0.73, 0.78) | 0.74 (0.72, 0.77) | ||||
| New Method 新方法 | 0.75 (0.72, 0.78) | 0.74 (0.71, 0.77) | ||||
Estimate
(1) 估计Standard error estimate
(2) 标准误差估计
p-value
(3) p 值The second data set for illustration is from a recent cancer study [20]. One primary goal of the study was to evaluate the prognostic value of a new gene signature in predicting the time to death or metastasis for breast cancer patients. An important clinical implications for establishing a risk score system is to identify future patients who may benefit from adjuvant systemic, but potentially toxic, therapies. The details of participants in the study are given in van’t Veer et al. [21] and van de Vijver et al. [22]. The data set for analysis consists of 295 breast cancer patient records from the Netherlands Cancer Institute. Our goal is to evaluate the prediction of patient survival based on the patients’ baseline covariates consisting of the new gene score and other conventional markers including age and estrogen receptor status. The Kaplan-Meier curves for the event time and the censoring time are given in Figure 2. Note that at Year 15, the survival rate is 0.61, the size of the risk set is 19, and there were no deaths beyond this time point. (http://microarray-pubs.stanford.edu/wound_NKI/explore.html).
第二个用于说明的数据集来自最近的一项癌症研究 [ 20]。该研究的一个主要目标是评估新基因特征在预测乳腺癌患者死亡或转移时间方面的预后价值。建立风险评分系统的一个重要临床意义是确定未来可能从辅助全身治疗(但可能具有毒性)治疗中受益的患者。van't Veer 等人 [ 21] 和 van de Vijver 等人 [ 22] 提供了研究参与者的详细信息。用于分析的数据集包括来自荷兰癌症研究所的 295 份乳腺癌患者记录。我们的目标是根据患者的基线协变量评估患者生存率的预测,这些协变量由新基因评分和其他常规标志物(包括年龄和雌激素受体状态)组成。事件时间和删失时间的 Kaplan-Meier 曲线如图 2 所示。请注意,在第 15 年,存活率为 0.61,风险集的大小为 19,并且在此时间点之后没有死亡。( http://microarray-pubs.stanford.edu/wound_NKI/explore.html)。
Figure 2. 图 2.

Estimates for survival functions for death and censoring variables with breast cancer data.
使用乳腺癌数据估计死亡和删失变量的生存函数。
We fit the data with two working Cox’s proportional hazards models. The covariate vector Z for the first model consists of only age and estrogen receptor (ER: positive or negative). The resulting risk score β̂′Z is
我们使用两个有效的 Cox 比例风险模型拟合数据。第一个模型的协变量向量 Z 仅包含年龄和雌激素受体 (ER:阳性或阴性)。得到的风险评分 β̂′Z 为
In the second model, we included the gene score variable (GS), age and ER. The risk score with the second model is
在第二个模型中,我们包括基因评分变量 (GS) 、年龄和 ER。第二个模型的风险评分为
In Table 3, we report the point and interval estimates of Cτ for both models with various τ. Our standard error estimates tend to be larger than those from the conventional C-statistic especially for the case when τ = 15. To examine the performance of the new proposal, we conducted a simulation study. The details are given in the next subsection.
在表 3 中,我们报告了两个模型具有不同 τ 的 C τ 的点和区间估计值。我们的标准误差估计值往往大于传统 C 统计量的标准误差估计值,尤其是在 τ = 15 的情况下。为了检查新提案的性能,我们进行了一项模拟研究。详细信息将在下一小节中给出。
Table 3. 表 3.
Point estimates (Est), standard error estimates (SE) and 0.95 confidence intervals (CI) for Cτ with breast cancer data
τ C 的点估计值 (Est)、标准误差估计值 (SE) 和 0.95 置信区间 (CI) 与乳腺癌数据
| C-index C 指数 | New Method 新方法 | Conventional 协定的 | ||||
|---|---|---|---|---|---|---|
| τ | Est 东 | SE 她自己 | CI 那里 | Est 东 | SE 她自己 | CI 那里 |
| Without Gene Score Model 无基因评分模型 | ||||||
| 6 | 0.66 | 0.04 | (0.58, 0.74) | 0.68 | 0.04 | (0.60, 0.76) |
| 8 | 0.65 | 0.04 | (0.58, 0.73) | 0.68 | 0.04 | (0.60, 0.75) |
| 10 | 0.65 | 0.04 | (0.57, 0.72) | 0.67 | 0.04 | (0.60, 0.74) |
| 15 | 0.62 | 0.05 | (0.53, 0.71) | 0.67 | 0.04 | (0.60, 0.74) |
| ∞* * ∞ | NA 上 | NA 上 | NA 上 | 0.67 | 0.04 | (0.60, 0.74) |
| With Gene Score Model 使用 Gene Score 模型 | ||||||
| 6 | 0.75 | 0.03 | (0.69, 0.82) | 0.76 | 0.03 | (0.69, 0.82) |
| 8 | 0.75 | 0.03 | (0.68, 0.81) | 0.75 | 0.03 | (0.69, 0.81) |
| 10 | 0.74 | 0.03 | (0.68, 0.80) | 0.75 | 0.03 | (0.69, 0.81) |
| 15 | 0.70 | 0.05 | (0.60, 0.79) | 0.75 | 0.03 | (0.69, 0.81) |
| ∞* * ∞ | NA 上 | NA 上 | NA 上 | 0.75 | 0.03 | (0.69, 0.81) |
Note that no event has been seen after t = 15 in the breast cancer data set. All usable pairs in the dataset are already utilized with τ = 15 for calculation of C-statistics. Thus, the estimates for τ = ∞ and those for τ = 15 are identical. With this data set, the censoring probability at t = 15 was 0.89.
* 请注意,在乳腺癌数据集中,t = 15 之后未观察到任何事件。数据集中的所有可用对都已用于 τ = 15 计算 C 统计量。因此,τ = ∞ 和 τ = 15 的估计值是相同的。对于此数据集,t = 15 时的删失概率为 0.89。
3.2. Simulation Study 3.2. 仿真研究
To examine the performance of the new and conventional methods, we conducted a numerical study under various practical settings. As described in section 2, our proposed inference procedure does not require the fitted model to be correct. Here, we used a working Cox regression model to obtain an estimated risk score, and make inferences about Cτ regardless of the adequacy of the working model. For instance, in one of the simulation settings, we considered two cases with survival time T generated from a Weibull regression model for the first case and from a log-normal regression model for the second case. For both models, we let Z = (AGE, ER, GS)′. We also considered three kinds of censoring: (a) type I censoring without staggered entry; (b) random censoring which is independent of survival time and covariates; and (c) random censoring which is independent of survival time conditional on the covariates. Note that in theory, the existing C-statistics may be valid only for (a). Our procedure is valid for (a) or (b). Setting (c) is explored to examine whether the proposed procedures are sensitive to violation of the independent censoring assumption, as suggested by the reviewers. We chose τ = 10 and 15, and n=100, 150, 200 and 300 for each simulation setting.
为了检查新方法和传统方法的性能,我们在各种实际设置下进行了一项数值研究。如第 2 节所述,我们提出的推理程序不要求拟合模型是正确的。在这里,我们使用了一个有效的 Cox 回归模型来获得估计的风险评分,并对 C τ 进行推断,而不管工作模型的充分性如何。例如,在其中一个模拟设置中,我们考虑了两个案例,其中生存时间 T 来自第一个案例的 Weibull 回归模型和第二个案例的对数正态回归模型。对于这两个模型,我们设 Z = (AGE, ER, GS)′。我们还考虑了三种类型的删失:(a) I 类删失,没有交错输入;(b) 随机删失,与生存时间和协变量无关;(c) 随机删失,它与以协变量为条件的生存时间无关。请注意,从理论上讲,现有的 C 统计量可能仅对 (a) 有效。我们的程序对 (a) 或 (b) 有效。探索设置 (c) 以检查拟议的程序是否对违反审查员建议的独立审查假设敏感。我们为每个仿真设置选择了 τ = 10 和 15,以及 n=100、150、200 和 300。
Firstly we simulated Z = (AGE, ER, GS)′, utilizing the breast cancer data. In particular, we generated ER status (positive or negative) from its empirical distribution, and then generated the corresponding (AGE, GS) from a multivariate normal distribution, MV N(μER, ΣER), where μER and ΣER are the empirical mean and variance-covariance matrix of (AGE, GS) conditioning on ER, respectively. For each given value of Z, we generated T from the aforementioned Weibull regression model for case (I) and the log-normal regression model for case (II). We mimicked the breast cancer study to create the true models for our simulation. Specifically, the regression coefficients estimates were obtained by fitting the observed breast cancer data for each model.
首先,我们利用乳腺癌数据模拟了 Z = (AGE, ER, GS)′。特别是,我们从其经验分布中生成了 ER 状态(正或负),然后从多元正态分布 MV N(μ ER , Σ ER ) 中生成了相应的 (AGE, GS),其中 μ ER 和 Σ ER 分别是 (AGE, GS) 条件对 ER 的经验平均值和方差协方差矩阵。对于每个给定的 Z 值,我们从上述案例 (I) 的 Weibull 回归模型和案例 (II) 的对数正态回归模型生成 T。我们模拟了乳腺癌研究,为我们的模拟创建了真实的模型。具体来说,回归系数估计值是通过拟合每个模型的观察到的乳腺癌数据来获得的。
With regard to generating censoring time, for censoring type (a), the censoring time D was set as τ + 0.1 for all subjects. For censoring type (b), we fitted the breast cancer data with a one-sample Weibull distribution (with two unknown parameters) to generate D from it. For censoring type (c), we fitted the breast cancer data with a Weibull regression model with the covariate Z = (AGE, ER, GS)′. About 45% of the subjects were censored by Year 10 and 70% by Year 15, which was similar to those from the breast cancer study.
关于生成删失时间,对于删失类型 (a),所有受试者的删失时间 D 都设置为 τ + 0.1。对于删失类型 (b),我们将乳腺癌数据与单样本 Weibull 分布(具有两个未知参数)拟合,以从中生成 D。对于删失类型 (c),我们使用协变量 Z = (AGE, ER, GS)′ 的 Weibull 回归模型拟合乳腺癌数据。大约 45% 的受试者在 10 年级时被删失,70% 的受试者在 15 年级时被删失,这与乳腺癌研究中的情况相似。
For all simulation configurations, we used a Cox regression model with Z = (AGE, ER, GS)′ as the working model to analyze each simulated data set regardless of whether the true model is the Weibull regression model or the log-normal regression model. Note that this model is correct under the aforementioned Weibull regression and incorrect under the log-normal regression model. For each configuration, we used the monte carlo method to calculate the true values of Cτ for the risk score obtained by fitting the working Cox model. Specifically, we generated one million data points of (T,Z) from each model. The true value for C10 = 0.724 and C15 = 0.718 when the Weibull regression model was true; C10 = 0.727 and C15 = 0.710 when the log-normal regression model was true.
对于所有模拟配置,我们使用 Z = (AGE, ER, GS)′ 作为工作模型的 Cox 回归模型来分析每个模拟数据集,无论真实模型是 Weibull 回归模型还是对数正态回归模型。请注意,此模型在上述 Weibull 回归下是正确的,而在对数正态回归模型下是不正确的。对于每种配置,我们使用蒙特卡洛方法计算通过拟合工作 Cox 模型获得的风险评分的 C τ 的真实值。具体来说,我们从每个模型生成了 100 万个 (T,Z) 数据点。当 Weibull 回归模型为 true 时,C 10 = 0.724 和 C 15 = 0.718 的真实值;C 10 = 0.727 和 C 15 = 0.710 当对数正态回归模型为 true 时。
For each setting, we then simulated 1000 independent realizations of {(Xi , Δi ,Zi)′, i = 1, … , n}. We fitted each simulated data set with the working Cox regression model and constructed a 0.95 confidence interval for Cτ given in (2.3). We also constructed the 0.95 confidence interval based on the conventional C-index given by Pencina and D’Agostino [13]. With the 1000 iterations, we obtained empirical coverage probabilities, average lengths of intervals, biases, and root mean square errors (rMSE).
对于每个设置,我们然后模拟了 {(X , Δ ,Z)′, i = 1, ... , n} 的 1000 个独立实现。我们用有效的 Cox 回归模型拟合每个模拟数据集,并为 ( 2.3) 中给出的 C τ 构建了一个 0.95 置信区间。我们还根据 Pencina 和 D'Agostino 给出的常规 C 指数构建了 0.95 置信区间 [ 13]。通过 1000 次迭代,我们获得了经验覆盖率概率、区间平均长度、偏差和均方根误差 (rMSE)。
Table 4 shows the results for the case where the working model is correct. When τ = 15 and n = 100 with independent censoring (b), for example, the coverage probabilities of the new and conventional methods are 0.944 and 0.876, respectively. The coverage probability of the new method is 0.946 and still close to the nominal level of 0.95 even under censoring type (c). Table 5 shows the results for the case where the fitted working model is not correct. For τ = 15 and n = 100, the coverage probabilities of the new method are 0.947 and 0.945 under independent and conditionally independent censoring, respectively. On the other hand, those of the conventional method are 0.771 and 0.774, respectively.
表 4 显示了工作模型正确情况下的结果。例如,当 τ = 15 且 n = 100 且具有独立删失 (b) 时,新方法和传统方法的覆盖率概率分别为 0.944 和 0.876。新方法的覆盖率为 0.946,即使在删失类型 (c) 下也仍然接近 0.95 的标称水平。表 5 显示了拟合工作模型不正确的情况的结果。对于 τ = 15 和 n = 100,新方法在独立和条件独立删失下的覆盖率概率分别为 0.947 和 0.945。另一方面,传统方法的 10 分值分别为 0.771 和 0.774。
Table 4. 表 4.
Coverage probabilities and average length of 0.95 confidence intervals, bias, and root mean square error (rMSE) for Cτ with τ = 10 and 15, based on 1000 of iterations for a working Cox’s model with (AGE, ER, GS), when the true model is (I) the Weibull regression model with AGE, ER and GS.
τ = 10 和 15 的 C τ 的覆盖率概率和 0.95 个置信区间、偏差和均方根误差 (rMSE) 的平均长度,基于具有 (AGE, ER, GS) 的工作 Cox 模型的 1000 次迭代,当真实模型是 (I) 具有 AGE、ER 和 GS 的 Weibull 回归模型时。
| Coverage 覆盖 | Ave. Length 平均长度 | Bias 偏见 | rMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| τ | Censoring 审查 | N | (1) | (2) | (1) | (2) | (1) | (2) | (1) | (2) |
| 10 | (a) Degenerate (a) 堕落 | 100 | 0.951 | 0.913 | 0.214 | 0.176 | 0.008 | 0.008 | 0.047 | 0.047 |
| 150 | 0.945 | 0.917 | 0.162 | 0.145 | 0.008 | 0.008 | 0.038 | 0.038 | ||
| 200 | 0.948 | 0.934 | 0.136 | 0.126 | 0.005 | 0.005 | 0.033 | 0.033 | ||
| 300 | 0.942 | 0.934 | 0.108 | 0.103 | 0.003 | 0.003 | 0.027 | 0.027 | ||
| (b) Independent (b) 独立 | 100 | 0.948 | 0.896 | 0.241 | 0.196 | 0.011 | 0.015 | 0.053 | 0.055 | |
| 150 | 0.952 | 0.903 | 0.184 | 0.163 | 0.007 | 0.010 | 0.043 | 0.044 | ||
| 200 | 0.942 | 0.914 | 0.152 | 0.141 | 0.009 | 0.012 | 0.037 | 0.039 | ||
| 300 | 0.954 | 0.938 | 0.122 | 0.118 | 0.003 | 0.007 | 0.029 | 0.030 | ||
| (c) Cond. Independent (c) 独立于条件 | 100 | 0.948 | 0.892 | 0.241 | 0.196 | 0.011 | 0.015 | 0.053 | 0.055 | |
| 150 | 0.951 | 0.898 | 0.184 | 0.163 | 0.007 | 0.010 | 0.043 | 0.044 | ||
| 200 | 0.946 | 0.916 | 0.152 | 0.142 | 0.009 | 0.012 | 0.037 | 0.039 | ||
| 300 | 0.954 | 0.937 | 0.122 | 0.118 | 0.003 | 0.007 | 0.029 | 0.030 | ||
| 15 | (a) Degenerate (a) 堕落 | 100 | 0.951 | 0.912 | 0.174 | 0.149 | 0.006 | 0.006 | 0.040 | 0.040 |
| 150 | 0.945 | 0.925 | 0.134 | 0.123 | 0.007 | 0.007 | 0.032 | 0.032 | ||
| 200 | 0.956 | 0.938 | 0.113 | 0.107 | 0.003 | 0.003 | 0.027 | 0.027 | ||
| 300 | 0.956 | 0.944 | 0.091 | 0.087 | 0.002 | 0.002 | 0.022 | 0.022 | ||
| (b) Independent (b) 独立 | 100 | 0.944 | 0.876 | 0.271 | 0.191 | 0.011 | 0.019 | 0.059 | 0.055 | |
| 150 | 0.952 | 0.896 | 0.207 | 0.159 | 0.007 | 0.015 | 0.048 | 0.045 | ||
| 200 | 0.932 | 0.892 | 0.172 | 0.138 | 0.007 | 0.017 | 0.042 | 0.040 | ||
| 300 | 0.950 | 0.926 | 0.137 | 0.115 | 0.003 | 0.012 | 0.033 | 0.031 | ||
| (c) Cond. Independent (c) 独立于条件 | 100 | 0.946 | 0.872 | 0.271 | 0.192 | 0.011 | 0.020 | 0.059 | 0.056 | |
| 150 | 0.952 | 0.894 | 0.206 | 0.159 | 0.007 | 0.015 | 0.048 | 0.045 | ||
| 200 | 0.942 | 0.881 | 0.173 | 0.139 | 0.008 | 0.017 | 0.043 | 0.040 | ||
| 300 | 0.951 | 0.925 | 0.137 | 0.115 | 0.004 | 0.012 | 0.033 | 0.031 | ||
New Method
(1) 新方法Conventional
(2) 协定的Table 5. 表 5.
Coverage probabilities and average length of 0.95 confidence intervals, bias, and root mean square error (rMSE) for Cτ with τ = 10 and 15, based on 1000 of iterations for a working Cox’s model with (AGE, ER, GS), when the true model is (II) the log-normal regression model with AGE, ER and GS.
τ = 10 和 15 的 C τ 的覆盖率概率和 0.95 个置信区间、偏差和均方根误差 (rMSE) 的平均长度,基于具有 (AGE, ER, GS) 的工作 Cox 模型的 1000 次迭代,当真实模型是 (II) 具有 AGE、ER 和 GS 的对数正态回归模型时。
| Coverage 覆盖 | Ave. Length 平均长度 | Bias 偏见 | rMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| τ | Censoring 审查 | N | (1) | (2) | (1) | (2) | (1) | (2) | (1) | (2) |
| 10 | a) Degenerate a) 退化 | 100 | 0.947 | 0.909 | 0.201 | 0.165 | 0.009 | 0.009 | 0.045 | 0.045 |
| 150 | 0.949 | 0.923 | 0.153 | 0.137 | 0.007 | 0.007 | 0.037 | 0.037 | ||
| 200 | 0.951 | 0.931 | 0.128 | 0.119 | 0.006 | 0.006 | 0.031 | 0.031 | ||
| 300 | 0.953 | 0.945 | 0.102 | 0.097 | 0.005 | 0.005 | 0.025 | 0.025 | ||
| (b) Independent (b) 独立 | 100 | 0.947 | 0.831 | 0.230 | 0.179 | 0.013 | 0.028 | 0.050 | 0.056 | |
| 150 | 0.950 | 0.858 | 0.176 | 0.150 | 0.007 | 0.024 | 0.041 | 0.046 | ||
| 200 | 0.947 | 0.850 | 0.146 | 0.130 | 0.007 | 0.023 | 0.036 | 0.041 | ||
| 300 | 0.926 | 0.822 | 0.116 | 0.106 | 0.006 | 0.023 | 0.030 | 0.036 | ||
| (c) Cond. Independent (c) 独立于条件 | 100 | 0.945 | 0.837 | 0.230 | 0.179 | 0.013 | 0.028 | 0.050 | 0.056 | |
| 150 | 0.942 | 0.859 | 0.175 | 0.150 | 0.008 | 0.024 | 0.042 | 0.046 | ||
| 200 | 0.950 | 0.853 | 0.146 | 0.130 | 0.007 | 0.023 | 0.036 | 0.041 | ||
| 300 | 0.928 | 0.813 | 0.116 | 0.106 | 0.006 | 0.023 | 0.030 | 0.036 | ||
| 15 | a) Degenerate a) 退化 | 100 | 0.953 | 0.921 | 0.170 | 0.144 | 0.006 | 0.006 | 0.039 | 0.039 |
| 150 | 0.960 | 0.935 | 0.131 | 0.119 | 0.004 | 0.004 | 0.031 | 0.031 | ||
| 200 | 0.960 | 0.945 | 0.111 | 0.103 | 0.003 | 0.003 | 0.026 | 0.026 | ||
| 300 | 0.949 | 0.944 | 0.088 | 0.085 | 0.002 | 0.002 | 0.022 | 0.022 | ||
| (b) Independent (b) 独立 | 100 | 0.947 | 0.771 | 0.263 | 0.175 | 0.011 | 0.043 | 0.060 | 0.063 | |
| 150 | 0.949 | 0.789 | 0.201 | 0.146 | 0.008 | 0.039 | 0.046 | 0.054 | ||
| 200 | 0.943 | 0.751 | 0.168 | 0.127 | 0.007 | 0.038 | 0.041 | 0.050 | ||
| 300 | 0.944 | 0.683 | 0.135 | 0.104 | 0.004 | 0.038 | 0.033 | 0.047 | ||
| (c) Cond. Independent (c) 独立于条件 | 100 | 0.945 | 0.774 | 0.264 | 0.175 | 0.011 | 0.043 | 0.060 | 0.063 | |
| 150 | 0.944 | 0.788 | 0.200 | 0.146 | 0.009 | 0.039 | 0.046 | 0.055 | ||
| 200 | 0.937 | 0.743 | 0.168 | 0.127 | 0.007 | 0.038 | 0.041 | 0.050 | ||
| 300 | 0.939 | 0.682 | 0.135 | 0.104 | 0.005 | 0.038 | 0.033 | 0.047 | ||
New Method
(1) 新方法Conventional
(2) 协定的In general, we find that the new interval estimation procedure performs well with relatively small sample size, regardless of the adequacy of the fitted model. Furthermore, the procedure is not sensitive to violation of the covariate independent censoring assumption with empirical coverage levels practically identical to their nominal counterparts under various situations. The conventional method proposed by Pencina and D’Agostino [13] performs well when the censoring distribution is a degenerate distribution (Type I censoring without staggered entry).
一般来说,我们发现新的区间估计程序在相对较小的样本量下表现良好,而不管拟合模型的充分性如何。此外,该程序对违反协变量独立删失假设不敏感,在各种情况下,经验覆盖率水平几乎与它们的名义对应物相同。Pencina 和 D'Agostino [ 13] 提出的常规方法在删失分布是退化分布(没有交错输入的 I 型删失)时表现良好。
4. REMARKS 4. 备注
In this article, we show that the overall performance of a parametric or semi-parametric model in predicting the subject-level survival over an interval (0, τ) can be evaluated via a simple, unbiased estimation procedure for Cτ. Based on our numerical study, we find that the new estimation procedure is robust with respect to the choice of τ. However, if the pre-specified τ is “too” large such that very few events were observed or very few study subjects were followed beyond this time point, the standard error estimate for Ĉτ can be quite large, reflecting a high degree of uncertainty of our inferences about Cτ. For this case, one should cautiously utilize the fitted model for prediction over this large time interval.
在本文中,我们表明参数或半参数模型在预测区间 (0, τ) 内受试者水平生存率的整体性能可以通过简单、无偏的 C τ 估计程序来评估。根据我们的数值研究,我们发现新的估计程序在 τ 的选择方面是稳健的。但是,如果预先指定的 τ “太”大,以至于观察到的事件非常少,或者在此时间点之后跟踪的研究对象非常少,则 Ĉ 的标准误差估计 τ 可能相当大,反映了我们对 C τ 的推断的高度不确定性。对于这种情况,应该谨慎地利用拟合模型在这个大时间间隔内进行预测。
There are various C-statistics proposed in the literature. With the same technique utilized in this article, one may modify these statistics accordingly so that they estimate concordance measures which are free of the study-specific censoring distribution. The computer code for implementing the new inference procedure can be downloaded from (http://bcb.dfci.harvard.edu/~huno).
文献中提出了各种 C 统计量。使用本文中使用的相同技术,可以相应地修改这些统计数据,以便他们估计不受研究特定删失分布影响的一致性度量。用于实现新推理过程的计算机代码可以从 ( http://bcb.dfci.harvard.edu/~huno) 下载。
For the new proposal, we assume that the censoring distribution is independent of the covariates. This assumption is not unreasonable in a well-executed clinical study, especially when there are no competing risks for observing the endpoint (for example, death or a composite clinical endpoint) and the event times are possibly censored mainly due to administrative censoring. When the covariate vector can be discretized, our new procedure can be modified easily using stratified Kaplan-Meier estimates for the censoring. When some of the covariates are continuous, one needs to assume a model for censoring distribution and use the resulting estimated distribution of the censoring to construct a new C-statistic. In theory, the validity of the resulting estimators depends on the adequacy of the model. On the other hand, based on the results from our simulation study, it appears that our proposal is quite robust even when the censoring is dependent on the covariates.
对于新提案,我们假设删失分布独立于协变量。在执行良好的临床研究中,这种假设并非不合理,尤其是当观察终点没有竞争风险(例如,死亡或复合临床终点)并且事件时间可能主要由于行政审查而被删失时。当协变量向量可以离散化时,我们的新程序可以使用分层 Kaplan-Meier 估计进行删失轻松修改。当某些协变量是连续的时,需要假设一个删失分布模型,并使用删失的结果估计分布来构建新的 C 统计量。从理论上讲,所得估计量的有效性取决于模型的充分性。另一方面,根据我们的仿真研究结果,即使删失取决于协变量,我们的提议似乎也相当稳健。
In this article, we showed an inference procedure not only for Cτ but also for the difference between two Cτ ’s for comparing two competing prediction models. Although C-statistics are commonly used for quantifying the predictability of working models, they are not sensitive for capturing overall added values from a new marker on top of conventional predictors [11, 13]. Alternatively, one might use measures such as explained variation for survival data to compare two models [7]. If the model is correct, the likelihood based measures may be more sensitive in detecting differences in prediction ability, compared to rank-based measures such as C-indexes. Recently, alternative statistical estimation procedures were proposed for comparing prediction models [23, 24], which may be utilized to quantify incremental values. Further research is needed for developing intuitively interpretable and sensitive methods for comparing prediction models.
在本文中,我们不仅展示了 C τ 的推理程序,还展示了两个 C τ 之间的差异,用于比较两个竞争的预测模型。尽管 C 统计量通常用于量化工作模型的可预测性,但它们对于在传统预测变量之上捕获新标记的总体附加值并不敏感 [ 11, 13]。或者,人们可以使用诸如生存数据的解释变异等措施来比较两个模型 [ 7]。如果模型正确,则与基于排名的度量(如 C 指数)相比,基于似然的度量在检测预测能力的差异时可能更敏感。最近,提出了替代统计估计程序来比较预测模型 [ 23, 24],可用于量化增量值。需要进一步的研究来开发直观可解释和敏感的预测模型比较方法。
Acknowledgments 确认
The authors are grateful to the associate editor, three referees, and the editor for insightful comments on the article. This work was supported in part by grants R01-GM079330, R01-AI052817, and N01-HC-25195 from the NIH.
作者感谢副主编、三位审稿人和编辑对文章的深刻评论。这项工作部分得到了 NIH 的 R01-GM079330、R01-AI052817 和 N01-HC-25195 的资助。
APPENDIX A: LARGE SAMPLE PROPERTIES OF Ĉτ
附录 A:Ĉ τ 的大样本属性
Throughout, we assume that the non-separable condition for (T,Z) given in section 2 holds, and thus β0 is the unique solution to the limit of the following partial likelihood score equation,
在整个过程中,我们假设第 2 节中给出的 (T,Z) 的不可分条件成立,因此 β 0 是以下偏似然得分方程极限的唯一解,
where Ni(t) = I(Xi ≤ t, Δi = 1), Yi(t) = I(Xi ≥ t). We assume that β0 lies in a compact parameter space and the joint density of (T, Z) is continuous and bounded. To show the consistency of Ĉτ , we first note that
其中 N(t) = I(X ≤ t, Δ = 1), Y(t) = I(X ≥ t)。我们假设 β 0 位于一个紧凑的参数空间中,并且 (T, Z) 的关节密度是连续的和有界的。为了显示 Ĉ τ 的一致性,我们首先注意到
| (A.1) (答 1) |
where A(β) = − {∂E(U(β))/∂β}−1 [25].
其中 A(β) = − {∂E(U(β))/∂β} −1 [ 25]。
Now, for a fixed β, let
现在,对于固定β,让
It follows from the uniform consistency of Ĝ(·), the convergence of β̂ to β0, and a uniform law of large numbers for U-processes [26], that Ĉτ converges to Cτ(β0) in probability as n → ∞. On the other hand, it follows from the asymptotic expansion of β̂ given in (A.1) that Cτ(β0) − Cτ = O(n−1). Thus, Ĉτ − Cτ → 0 in probability.
根据 Ĝ(·) 的均匀一致性、β̂ 与 β 0 的收敛以及 U 过程的均匀大数定律 [ 26],Ĉ τ 收敛到 C τ (β 0 ) 的概率为 n → ∞。另一方面,根据 ( A.1) 中给出的 β̂ 的渐近展开,可以得出 C τ (β 0 ) − C τ = O(n −1 )。因此,Ĉ τ − C τ 的概率→ 0。
To approximate the distribution of
要近似
we first obtain asymptotic expansions for W(β) = n1/2{Ĉτ(β) − Cτ(β)}, where Ĉτ(β) is obtained by replacing β̂ in Ĉτ of (2.4) with β. To this end, we write W(β) = Wa(β) + Wb(β), where
我们首先获得 W(β) = n 1/2 {Ĉ τ (β) − C τ (β)},其中 Ĉ τ (β) 是通过将 ( 2.4) 的 Ĉ τ 中的 β̂ 替换为 β 获得的。为此,我们写 W(β) = W a (β) + W b (β),其中
and Iij(τ) = I(Xi < Xj, Xi < τ)Δi. Now, it follows from the standard asymptotic theory for the Kaplan Meier estimator [27],
和 I ij (τ) = I(X < X, X < τ)Δ。现在,它遵循 Kaplan Meier 估计器 [ 27] 的标准渐近理论,
and ŴG(t) converges weakly to a zero-mean Gaussian process indexed by t for t ≤ τ, where
和 Ŵ G (t) 弱收敛到一个零均值高斯过程,该过程由 t 对 t ≤ τ 进行索引,其中
where p(τ) = P(T1 < T2, T1 < τ). Furthermore,
其中 p(τ) = P(T 1 < T 2 , T 1 < τ)。此外
where 哪里
By a uniform law of large numbers for U-processes [26] and the uniform consistency of Ĝ(·), we have
根据 U 过程的大数统一定律 [ 26] 和 Ĝ(·) 的统一一致性,我们得到
where 哪里
This, coupled with the weak convergence of ŴG(t), implies that
这与 Ŵ G (t) 的弱收敛相结合,意味着
Therefore, 因此
where νij(β) = (Vij(β) + Vij(β))/2,
其中 ν ij (β) = (V ij (β) + V ij (β)))/2,
and φij(β) = ∫ {ψi(t) + ψj(t)} dγ(t, β). It then follows from a functional central limit theorem for U-processes that W(β) converges weakly to a zero-mean Gaussian process. This, together with the continuity of Cτ(β) and the asymptotic expansion of n1/2(β̂ − β0), implies that
和 φ ij (β) = ∫ {ψ(t) + ψ(t)} dγ(t, β)。然后,根据 U 过程的泛函中心极限定理,W(β) 弱收敛到零均值高斯过程。这与 C τ (β) 的连续性和 n 1/2 (β̂ − β 0 ) 的渐近展开一起意味着
| (A.2) (答 2) |
where Ċτ(β) = ∂Cτ (β)/∂β and
其中 Ċ τ (β) = ∂C τ (β)/∂β 且
This, together with the standard asymptotic theory of U-statistics, W is asymptotically normal with mean 0 and variance E(W12W13).
这与 U 统计的标准渐近理论一起,W 是渐近正态的,均值为 0 且方差为 E(W 12 W )。 13
To estimate the variance of W, we utilize a perturbation-resampling method which has been successfully used for handling numerous inference problems in survival analysis [29, 30]. To be specific, let {Ξi, i = 1, … n} be a set of n iid random variables from a known distribution with mean 1 and variance 1. For a large n, we can approximate W with the conditional distribution (conditional on the data) of
为了估计 W 的方差,我们利用了一种扰动重采样方法,该方法已成功用于处理生存分析中的许多推理问题 [ 29, 30]。具体来说,设 {Ξ, i = 1, ...n} 是来自已知分布的一组 n 个 iid 随机变量,均值为 1,方差为 1。对于一个大的 n,我们可以用条件分布(以数据为条件)来近似 W
| (A.3) (答 3) |
where 哪里
where
其中
Note that only the random quantity in W̃ is {Ξi, i = 1,…,n}. The unknown quantities are replaced with their empirical counterparts. The distribution of W̃ (and therefore the distribution of W) can be approximated by generating a large number of realized random samples from {Ξi, i = 1,…n}.
请注意,只有 W̃ 中的随机量是 {Ξ, i = 1,...,n}。未知量被其经验对应物替换。W̃ 的分布(以及 W 的分布)可以通过从 {Ξ, i = 1 生成大量已实现的随机样本来近似,...n}.
APPENDIX B: LARGE SAMPLE APPROXIMATION TO Wξ
附录 B:大样本近似值 W ξ
From (A.2), Wξ is denoted by
从 ( A.2) 开始,W ξ 用
References 引用
-
1.Anderson KM, Odell PM, Wilson PW, Kannel WB. Cardiovascular risk profiles. American Heart Journal. 1991;121:293–8. doi: 10.1016/0002-8703(91)90861-b. [DOI] [PubMed] [Google Scholar]
1.Anderson KM、Odell PM、Wilson PW、Kannel WB。心血管风险概况。美国心脏杂志。1991;121:293–8.doi: 10.1016/0002-8703(91)90861-b. [ DOI] [ PubMed] [ Google 学术搜索] -
2.D’Agostino RB, Vasan RS, Pencina MJ, Wolf PA, Cobain MR, Massaro JM, Kannel WB. General cardiovascular risk profile for use in primary care: The Framingham Heart Study. Circulation. 2008;117(6):743–53. doi: 10.1161/CIRCULATIONAHA.107.699579. [DOI] [PubMed] [Google Scholar]
2.D'Agostino RB、Vasan RS、Pencina MJ、Wolf PA、Cobain MR、Massaro JM、Kannel WB。用于初级保健的一般心血管风险概况:弗雷明汉心脏研究。流通。2008;117(6):743–53.doi: 10.1161/CIRCULATIONAHA.107.699579.[ DOI][ 公共医学][ 谷歌学术搜索] -
3.Shariat SF, Karakiewicz PI, Roehrborn CG, Kattan MW. An updated catalog of prostate cancer predictive tools. Cancer. 2008;113(11):3075–99. doi: 10.1002/cncr.23908. [DOI] [PubMed] [Google Scholar]
3.Shariat SF、Karakiewicz PI、Roehrborn CG、Kattan MW。前列腺癌预测工具的更新目录。癌症。2008;113(11):3075–99.doi:10.1002/cncr.23908。[ DOI][ 公共医学][ 谷歌学术搜索] -
4.Parikh NI, Pencina MJ, Wang TJ, Benjamin EJ, Lanier KJ, Levy D, D’Agostino RB, Sr, Kannel WB, Vasan RS. A risk score for predicting near-term incidence of hypertension: the Framingham Heart Study. Annals of Internal Medicine. 2008;148(2):102–10. doi: 10.7326/0003-4819-148-2-200801150-00005. [DOI] [PubMed] [Google Scholar]
4.Parikh NI, Pencina MJ, Wang TJ, Benjamin EJ, Lanier KJ, Levy D, D'Agostino RB, Sr, Kannel WB, Vasan RS.预测近期高血压发病率的风险评分:弗雷明汉心脏研究。内科年鉴。2008;148(2):102–10.doi: 10.7326/0003-4819-148-2-200801150-00005.[ DOI][ 公共医学][ 谷歌学术搜索] -
5.Bamber D. The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. Journal of Mathematical Psychology. 1975;12:387–415. [Google Scholar]
5.班博 D.序数显性图上方的区域和受试者操作特征图下方的区域。数学心理学杂志。1975;12:387–415.[ 谷歌学术搜索] -
6.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
6.Hanley JA,麦克尼尔 BJ。受试者工作特征 (ROC) 曲线下面积的含义和用途。放射学。1982;143:29–36.doi: 10.1148/radiology.143.1.7063747.[ DOI][ 公共医学][ 谷歌学术搜索] -
7.Korn EL, Simon R. Measures of explained variation for survival data. Statistics in Medicine. 1990;9:487–503. doi: 10.1002/sim.4780090503. [DOI] [PubMed] [Google Scholar]
7.Korn EL, Simon R. 生存数据解释变异的测量。医学统计。1990;9:487–503.doi: 10.1002/sim.4780090503.[ DOI][ 公共医学][ 谷歌学术搜索] -
8.Hielscher T, Zucknick M, Werft W, Benner A. On the prognostic value of survival models with application to gene expression signatures. Statistics in Medicine. 2010;29:818–829. doi: 10.1002/sim.3768. [DOI] [PubMed] [Google Scholar]
8.Hielscher T, Zucknick M, Werft W, 本纳 A.关于应用于基因表达特征的生存模型的预后价值。医学统计。2010;29:818–829.doi:10.1002/sim.3768。[ DOI][ 公共医学][ 谷歌学术搜索] -
9.Harrell FE, Califf RM, Pryor DB, Lee KL, Rosati RA. Evaluating the yield of medical tests. Journal of the American Medical Association. 1982;247:2543–46. [PubMed] [Google Scholar]
9.Harrell FE, Califf RM, Pryor DB, Lee KL, Rosati RA.评估医学检查的检出率。美国医学会杂志。1982;247:2543–46.[ 公共医学][ 谷歌学术搜索] -
10.Harrell FE, Lee KL, Califf RM, Pryor DB, Lee KL, Rosati RA. Regression modeling strategies for improved prognostic prediction. Statistics in Medicine. 1984;3:143–52. doi: 10.1002/sim.4780090503. [DOI] [PubMed] [Google Scholar]
10.Harrell FE, Lee KL, Califf RM, Pryor DB, Lee KL, Rosati RA.改进预后预测的回归建模策略。医学统计。1984;3:143–52.doi: 10.1002/sim.4780090503.[ DOI][ 公共医学][ 谷歌学术搜索] -
11.Harrell FE, Lee KL, Mark DB. Tutorial in Biostatistics: Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Statistics in Medicine. 1996;15:361–87. doi: 10.1002/(SICI)1097-0258(19960229)15:4¡361∷AID-SIM168¿3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
11.Harrell FE, Lee KL, Mark DB.生物统计学教程:多变量预后模型:开发模型、评估假设和充分性以及测量和减少错误的问题。医学统计。1996;15:361–87.doi: 10.1002/(SICI)1097-0258(19960229)15:4361∷AID-SIM168¿3.0.CO;2-4.[ DOI][ 公共医学][ 谷歌学术搜索] -
12.Brown BW, Hollander M, Korwar RM. Nonparametric tests of independence for censored data, with applications to heart transplant studies. In: Proschan F, Serfling RJ, editors. Reliability and Biometry. SIAM; Philadelphia: 1974. [Google Scholar]
12.Brown BW, Hollander M, Korwar RM. 删失数据独立性的非参数检验,应用于心脏移植研究。在:Proschan F,Serfling RJ,编辑。可靠性和生物测量。暹罗;费城:1974 年。[ 谷歌学术搜索] -
13.Pencina MJ, D’Agostino RB. Overall C as a measure of discrimination in survival analysis: model specific population value and confidence interval estimation. Statistics in Medicine. 2004;23:2109–23. doi: 10.1002/sim.1802. [DOI] [PubMed] [Google Scholar]
13.Pencina MJ, D'Agostino RB.总体 C 作为生存分析中区分的衡量标准:对特定总体值和置信区间估计进行建模。医学统计。2004;23:2109–23.doi:10.1002/sim.1802。[ DOI][ 公共医学][ 谷歌学术搜索] -
14.Heagerty PJ, Zheng Y. Survival model predictive accuracy and ROC curves. Biometrics. 2005;61:92–105. doi: 10.1111/j.0006-341X.2005.030814.x. [DOI] [PubMed] [Google Scholar]
14.Heagerty PJ, Zheng Y. 生存模型预测准确性和 ROC 曲线。生物测定学。2005;61:92–105.doi: 10.1111/j.0006-341X.2005.030814.x.[ DOI][ 公共医学][ 谷歌学术搜索] -
15.Chambless LE, Diao G. Estimation of time-dependent area under the ROC curve for long-term risk prediction. Statistics in Medicine. 2006;25:3474–3486. doi: 10.1002/sim.2299. [DOI] [PubMed] [Google Scholar]
15.Chambless LE, Diao G. 用于长期风险预测的 ROC 曲线下时间依赖面积的估计。医学统计。2006;25:3474–3486.doi:10.1002/sim.2299。[ DOI][ 公共医学][ 谷歌学术搜索] -
16.Cai T, Pepe MS, Zheng Y, Lumley T, Jenny NS. The sensitivity and specificity of markers for event times. Biostatistics. 2006;72:182–97. doi: 10.1093/biostatistics/kxi047. [DOI] [PubMed] [Google Scholar]
16.Cai T, Pepe MS, Zheng Y, Lumley T, Jenny NS.事件时间标记的敏感性和特异性。生物统计学。2006;72:182–97.doi:10.1093/生物统计学/KXI047。[ DOI][ 公共医学][ 谷歌学术搜索] -
17.Gönen M, Heller G. Concordance probability and discriminatory power in proportional hazards regression. Biometrika. 2005;92:965–970. doi: 10.1093/biomet/92.4.965. [DOI] [Google Scholar]
17.Gönen M, Heller G. 比例风险回归中的一致性概率和判别能力。生物计量器。2005;92:965–970.doi:10.1093/biomet/92.4.965。[ DOI][ 谷歌学术搜索] -
18.Cox DR. Regression models and life tables (with Discussion) Journal of the Royal Statistical Society, Ser B. 1972;34:187–220. [Google Scholar]
18.Cox DR. 回归模型和寿命表(含讨论),皇家统计学会杂志,Ser B. 1972;34:187–220.[ 谷歌学术搜索] -
19.Cheng SC, Wei LJ, Ying Z. Analysis of transformation models with censored data. Biometrika. 1995;82:835–845. doi: 10.1093/biomet/82.4.835. [DOI] [Google Scholar]
19.Cheng SC, Wei LJ, Ying Z. 删失数据的转换模型分析。生物计量器。1995;82:835–845.doi:10.1093/biomet/82.4.835。[ DOI][ 谷歌学术搜索] -
20.Chang HY, Nuyten DSA, Sneddon JB, Hastie T, Tibshirani R, Sørlieb T, Dai H, He YD, van’t Veer LJ, Bartelinke H, van de Rijnj M, Brownb PO, van de Vijver MJ. Robustness, scalability, and integration of a wound-response gene expression signature in predicting breast cancer survival. PNAS. 2005;102:3738–43. doi: 10.1073/pnas.0409462102. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Chang HY, Nuyten DSA, Sneddon JB, Hastie T, Tibshirani R, Sørlieb T, Dai H, He YD, van't Veer LJ, Bartelinke H, van de Rijnj M, Brownb PO, van de Vijver MJ.伤口反应基因表达特征的稳健性、可扩展性和整合性在预测乳腺癌生存率方面的作用。美国国家科学院 (PNAS)。2005;102:3738–43.doi:10.1073/pnas.0409462102。[ DOI][ PMC 免费文章][ 公共医学][ 谷歌学术搜索] -
21.van’t Veer LJ, Dai H, van de Vijver MJ, He YD, Hart AA, Mao M, Peterse HL, van der Kooy K, Marton MJ, Witteveen AT. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415:530–6. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
21.van't Veer LJ, Dai H, van de Vijver MJ, He YD, Hart AA, 毛 M, 彼得斯 HL, 范德库伊 K, 马顿 MJ, 维特芬 AT.基因表达谱可预测乳腺癌的临床结果。自然界。2002;415:530–6.doi:10.1038/415530a。[ DOI][ 公共医学][ 谷歌学术搜索] -
22.van de Vijver MJ, He YD, van’t Veer LJ, Dai H, Hart AAM, Voskuil DW, Schreiber GJ, Peterse JL, Roberts C, Marton MJ, Parrish M, Atsma D, Witteveen A, Glas A, Delahaye L, van der Velde T, Bartelink H, Rodenhuis S, Rutgers ET, Friend SH, Bernards R. A gene-expression signature as a predictor of survival in breast cancer. The New England Journal of Medicine. 2002;347:1999–2009. doi: 10.1056/NEJMoa021967. [DOI] [PubMed] [Google Scholar]
22.van de Vijver MJ, He YD, van't Veer LJ, Dai H, Hart AAM, Voskuil DW, Schreiber GJ, Peterse JL, Roberts C, Marton MJ, Parrish M, Atsma D, Witteveen A, Glas A, Delahaye L, van der Velde T, Bartelink H, Rodenhuis S, Rutgers ET, Friend SH, Bernards R.基因表达特征作为乳腺癌生存率的预测因子。新英格兰医学杂志。2002;347:1999–2009.doi: 10.1056/NEJMoa021967.[ DOI][ 公共医学][ 谷歌学术搜索] -
23.Pencina MJ, D’Agostino RB, Sr, D’Agostino RB, Jr, Vasan RS. Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Statistics in Medicine. 2008;27:157–72. doi: 10.1002/sim.2929. [DOI] [PubMed] [Google Scholar]
23.Pencina MJ, D'Agostino RB, Sr, D'Agostino RB, Jr, Vasan RS.评估新标记物的附加预测能力:从 ROC 曲线下面积到重新分类及以后。医学统计。2008;27:157–72.doi:10.1002/sim.2929。[ DOI][ 公共医学][ 谷歌学术搜索] -
24.Cai T, Tian L, Lloyd-Jones DM, Wei LJ. Evaluating subject-level incremental values of new markers for risk classification rule. Harvard University Biostatistics Working Paper Series. 2008 doi: 10.1007/s10985-013-9272-6. Working Paper 91. http://www.bepress.com/harvardbiostat/paper91. [DOI] [PMC free article] [PubMed]
24.蔡 T, 田 L, Lloyd-Jones DM, 魏 LJ.评估风险分类规则的新标记的主题级增量值。哈佛大学生物统计学工作论文系列。2008 doi: 10.1007/s10985-013-9272-6.工作论文 91.http://www.bepress.com/harvardbiostat/paper91。[ DOI][ PMC 免费文章][ 公共医学] -
25.Hjort N. On inference in parametric survival data models. International Statistical Review. 1992;60:355–87. [Google Scholar]
25.约尔特 N.关于参数生存数据模型中的推理。国际统计评论。1992;60:355–87.[ 谷歌学术搜索] -
26.Nolan D, Pollard D. U-processes: Rates of convergence. The Annals of Statistics. 1987;15:780–99. [Google Scholar]
26.Nolan D, Pollard D. U 过程:收敛率。统计年鉴。1987;15:780–99.[ 谷歌学术搜索] -
27.Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. 2. Wiley; New York: 2002. [Google Scholar]
27.Kalbfleisch JD,Prentice RL。失效时间数据的统计分析。2. 威利;纽约:2002 年。[ 谷歌学术搜索] -
28.Nolan D, Pollard D. Functional limit theorems for U-processes. The Annals of Statistics. 1988;16:1291–98. [Google Scholar]
28.Nolan D, Pollard D. U 过程的泛函极限定理。统计年鉴。1988;16:1291–98.[ 谷歌学术搜索] -
29.Lin DY, Wei LJ, Ying Z. Checking the Cox model with cumulative sums of martingale-based residuals. Biometrika. 1993;80:557–72. doi: 10.1093/biomet/80.3.557. [DOI] [Google Scholar]
29.Lin DY, Wei LJ, Ying Z. 用基于马丁格尔的残差的累积和检查 Cox 模型。生物计量器。1993;80:557–72.doi:10.1093/biomet/80.3.557。[ DOI][ 谷歌学术搜索] -
30.Lin DY, Fleming TR, Wei LJ. Confidence bands for survival curves under the proportional hazards model. Biometrika. 1994;81:73–81. doi: 10.1093/biomet/81.1.73. [DOI] [Google Scholar]
30.林迪, 弗莱明 TR, 魏 LJ.比例风险模型下生存曲线的置信带。生物计量器。1994;81:73–81.doi:10.1093/biomet/81.1.73。[ DOI][ 谷歌学术搜索]


