Abstract 摘要
Skin effect, experimentally discovered in one dimension, describes the physical phenomenon that on an open chain, an extensive number of eigenstates of a non-Hermitian Hamiltonian are localized at the end(s) of the chain. Here in two and higher dimensions, we establish a theorem that the skin effect exists, if and only if periodic-boundary spectrum of the Hamiltonian covers a finite area on the complex plane. This theorem establishes the universality of the effect, because the above condition is satisfied in almost every generic non-Hermitian Hamiltonian, and, unlike in one dimension, is compatible with all point-group symmetries. We propose two new types of skin effect in two and higher dimensions: the corner-skin effect where all eigenstates are localized at corners of the system, and the geometry-dependent-skin effect where skin modes disappear for systems of a particular shape, but appear on generic polygons. An immediate corollary of our theorem is that any non-Hermitian system having exceptional points (lines) in two (three) dimensions exhibits skin effect, making this phenomenon accessible to experiments in photonic crystals, Weyl semimetals, and Kondo insulators.
皮肤效应在一维中被实验证明,描述了在开放链上,非厄米哈密顿算符的大量本征态被局域在链的末端。在二维及更高维度中,我们建立了一个定理,即当哈密顿算符的周期边界谱在复平面上覆盖有限区域时,皮肤效应存在。这个定理确立了该效应的普适性,因为几乎所有一般的非厄米哈密顿算符都满足上述条件,并且与所有点群对称性兼容,这与一维情况不同。我们提出了二维及更高维度中的两种新型皮肤效应:角皮肤效应,其中所有本征态都局域在系统的角落;以及几何依赖皮肤效应,其中特定形状的系统中皮肤模式消失,但在一般的多边形中出现。我们定理的一个直接推论是,在二维(三维)中具有异常点(线)的任何非厄米系统都会表现出皮肤效应,使得这种现象可以在光子晶体、Weyl半金属和康多绝缘体中进行实验。
Similar content being viewed by others
其他人正在查看相似的内容
Introduction 介绍
The study of non-Hermitian Hamiltonians, which can be regarded as the effective description of dissipative processes, can be traced back to the investigation of alpha decay, where real and imaginary parts of the complex energy are related to the experimentally observed energy level and decay rate1. When a lattice system is coupled with environments and has dissipations, e.g. photonic crystals having radiational loss2,3,4 and electronic systems having finite quasiparticle lifetime5,6, the non-Hermitian band theory becomes a conceptually simple and efficient approach7,8,9,10,11,12.
非厄米哈密顿量的研究可以看作是耗散过程的有效描述,可以追溯到对α衰变的研究,其中复能量的实部和虚部与实验观测到的能级和衰变速率相关。当晶格系统与环境耦合并具有耗散时,例如具有辐射损耗的光子晶体和具有有限准粒子寿命的电子系统,非厄米带理论成为一个概念上简单而高效的方法。
Skin effect13,14,15,16,17,18,19,20,21,22,23, a phenomenon unique to the non-Hermitian band theory, refers to the localization of eigenstates at the boundary, the number of which scales with the volume of the system. For example, in one dimension, all eigenstates of a non-Hermitian Hamiltonian can be localized at the ends of a chain13. This suggests the failure of Bloch’s theorem24,25, which states that eigenstates in the bulk are modulated plane waves. As Bloch’s theorem plays a fundamental role in the development of condensed-matter physics26, the emergence of skin effect indicates a new and possibly revolutionary direction. Especially, the skin effect has been observed experimentally in one-dimensional classical systems27,28,29, inspiring further studies on their higher dimensional generalizations14,30,31,32,33,34,35,36,37. However, a general theory for the higher-dimensional skin effect has not been established.
皮肤效应是非厄米带理论独特的现象,指的是本征态在边界处的局域化,其数量与系统体积成比例。例如,在一维情况下,非厄米哈密顿量的所有本征态可以局域在链的两端。这表明了布洛赫定理的失败,该定理指出体内的本征态是调制的平面波。由于布洛赫定理在凝聚态物理的发展中起着基础性的作用,皮肤效应的出现表明了一种新的、可能是革命性的方向。特别是,在一维经典系统中已经实验观察到了皮肤效应,这激发了对其高维推广的进一步研究。然而,关于高维皮肤效应的一般理论尚未建立。
Apart from the skin effect, another focus topic in non-Hermitian band systems is the exceptional point (or line)38,39,40,41,42,43,44,45,46,47 that refers to stable point-type (or line-type) non-Hermitian band degeneracy in the Brillouin zone. At the exceptional point, not only eigenvalues but also eigenstates of the Bloch Hamiltonian coalesce39. Many a novel phenomenon related to exceptional points has been predicted and observed47,48,49,50,51,52, such as the emergence of bulk-Fermi arc terminated at the exceptional points5,45. Since the bulk-boundary correspondence plays a central role in the development of topological phases53, it is natural to ask if there exists a non-Hermitian bulk-boundary correspondence in bands having exceptional points, analogous to the surface Fermi arc in the Weyl semimetals in the Hermitian counterpart54.
除了表面效应之外,非厄米带系统中的另一个重点研究课题是异常点(或线) 38,39,40,41,42,43,44,45,46,47 ,它指的是布里渊区中稳定的点状(或线状)非厄米带简并。在异常点处,布洛赫哈密顿量的本征值和本征态都融合在一起 39 。许多与异常点相关的新现象已经被预测并观测到 47,48,49,50,51,52 ,比如在异常点处终止的体态费米弧的出现 5,45 。由于体边对应在拓扑相位的发展中起着核心作用 53 ,自然而然地会问是否存在着与表面费米弧相似的非厄米带优势的体边对应 54 。
In this paper, we establish a theorem that reveals a universal bulk-boundary correspondence in two and higher dimensional non-Hermitian bands, as shown in Fig. 1. The “bulk” refers to the area of the spectrum of the Hamiltonian on the complex plane with periodic boundary condition, and “boundary” means the presence (absence) of the skin effect for open-boundary system of a generic shape. The theorem states that the skin effect appears if and only if the spectral area is nonzero. This skin effect is “universal” for three reasons: (i) a randomly generated local non-Hermitian Hamiltonian has the skin effect with probability one; (ii) the skin effect is, unlike in one dimension, compatible with all point-group symmetries and time-reversal symmetry, including complex-conjugate-type and transpose-type time-reversal symmetry in ref. 11; and (iii) it does not require any special geometry of the open-boundary system. We classify the universal skin effect into non-reciprocal skin effect and generalized reciprocal skin effect according to nonzero and zero current functional, respectively, and also propose the corner-skin effect and geometry-dependent-skin effect as representative phenomena of these two categories.
在本文中,我们建立了一个定理,揭示了二维及以上非厄米能带中的普适性体-边对应关系,如图1所示。这里的“体”指的是具有周期边界条件的哈密顿量在复平面上的能谱区域,“边”指的是具有一般形状的开边界系统中是否存在(不存在)皮肤效应。该定理表明,只有当能谱区域非零时,才会出现皮肤效应。这种皮肤效应具有三个“普适性”特征:(i)随机生成的局域非厄米哈密顿量具有皮肤效应的概率为1;(ii)与一维情况不同,皮肤效应与所有点群对称性和时间反演对称性兼容,包括复共轭型和转置型时间反演对称性;(iii)它不需要开边界系统的任何特殊几何形状。 我们根据非零和零电流功能将普适皮肤效应分为非互易皮肤效应和广义互易皮肤效应,并提出角皮肤效应和几何依赖皮肤效应作为这两个类别的代表现象。
图1:普遍皮肤效应定理。
a represents the Brillouin zone. b, d shows that if the spectral area of is nonzero, the skin effect will appear on some generic open-boundary geometries. c, e shows that when the spectral area of is zero, or forming one or several arcs on the complex plane, there is no skin effect under any geometry.
a代表布里渊区。b、d表示如果 的频谱区域非零,则在某些通用开放边界的几何结构上会出现皮肤效应。c、e表示当 的频谱区域为零,或在复平面上形成一个或多个弧时,任何几何结构下都没有皮肤效应。
A surprising corollary of our theorem is that the stable exceptional points8,41,43 imply the presence of skin effect. Because exceptional points have been either observed or proposed in meta-materials as well as in condensed matter, this corollary makes skin effect observable in known systems. We predict the geometry-dependent skin effect in the two-dimensional photonic crystal studied in ref. 45, and propose to observe this effect in the anomalous dynamics of wave packets.
我们定理的一个令人惊讶的推论是,稳定的异常点 8,41,43 意味着存在皮肤效应。由于异常点已经在介质材料和凝聚态中被观察或提出,这个推论使得已知系统中的皮肤效应可观测。我们预测在参考文献 45 中研究的二维光子晶体中存在几何相关的皮肤效应,并建议通过波包的异常动力学来观察这种效应。
Results 结果
Theorem: an equivalence between spectral area and skin effect
定理:光谱面积与皮肤效应之间存在等价关系
For generic one-dimensional non-Hermitian systems, the correspondence between the spectral shape and the skin effect has been derived17,18, i.e., when the Bloch spectrum is a loop-type (an arc-type), the skin effect appears (disappears).
对于一维非厄米系统,已经推导出了谱形状与表面效应之间的对应关系,即当布洛赫谱呈环状(弧状)时,表面效应出现(消失)。
Generalizing the correspondence to two dimensions, we note two main differences. One difference is in the periodic-boundary spectrum, Ei(k), where i is the band index and k the crystal momentum in the first Brillouin zone (BZ). Generally speaking, Ei(k) is a mapping from the d-dimensional torus to the complex plane, . When d = 1, the image of Ei(k) forms a loop; but when d > 1, the image is generically a continuum on , denoted by Ei(BZ). The area covered by Ei(BZ) on the complex plane is called the spectral area, denoted by Ai. Another difference is in the variety of open-boundary condition. There is only one geometry for an open system in one dimension, i.e., an open chain; but there are an infinite number of geometries in two dimensions such as triangle, rectangle and pentagon.
一般化到二维情况下,我们注意到两个主要的差异。一个差异在于周期边界谱E(k),其中i是能带指数,k是第一布里渊区(BZ)中的晶体动量。一般来说,E(k)是从d维环面到复平面的映射。当d = 1时,E(k)的图像形成一个环;但当d > 1时,图像通常是在BZ上的一个连续体,用E(BZ)表示。E(BZ)在复平面上覆盖的区域称为谱区域,用A表示。另一个差异在于开边界条件的多样性。在一维开放系统中只有一种几何形状,即开放链;但在二维中有无限多种几何形状,如三角形、矩形和五边形。
Now we are ready to state the theorem of universal skin effect: in the thermodynamic limit, the skin effect is present in a Hamiltonian having open boundary of generic geometry, if the spectral area is nonzero (Ai ≠ 0); vice versa, the skin effect is absent for all possible geometries, if the spectral area is zero (Ai = 0). The open boundary in the theorem refers to the fully open boundary condition in all spatial directions. As the periodic-boundary Hamiltonian describes the dynamics in the bulk, the theorem relates a bulk property (spectral area) to a boundary one (existence of skin modes). Fig. 1 shows some schematic examples. The complete proof of the theorem is provided in the Supplementary Note 1.
现在我们准备陈述普适皮肤效应的定理:在热力学极限下,如果哈密顿量具有一般几何形状的开放边界,并且谱面积非零(A ≠ 0),那么存在皮肤效应;相反,如果谱面积为零(A = 0),则所有可能的几何形状都不存在皮肤效应。定理中的开放边界指的是在所有空间方向上都完全开放的边界条件。由于周期边界的哈密顿量描述了体内的动力学,该定理将一个体内属性(谱面积)与一个边界属性(存在皮肤模式)相关联。图1展示了一些示意例子。关于定理的完整证明已在《补充说明1》中提供。
A brief outline of the proof is illustrated in Fig. 2. The theorem is obtained in three steps: step I establishes the equivalence relation between spectral area and spectral winding number of straight lines in the BZ; step II connects these nonzero spectral winding numbers with skin effect on the stripe geometry — the geometry with open boundary in only one direction and periodic boundary in other directions; step III illustrates that skin effect on stripe geometry implies skin effect on fully open-boundary geometry (i.e., the universal skin effect), which relies on a conjecture. The justification of this conjecture is discussed in the Supplementary Note 1.
证明的简要概述如图2所示。该定理分为三个步骤:第一步建立了布里渊区中直线的谱面积和谱绕数之间的等价关系;第二步将这些非零谱绕数与条纹几何体上的皮肤效应相联系——该几何体在一个方向上具有开放边界,在其他方向上具有周期性边界;第三步说明了条纹几何体上的皮肤效应意味着完全开放边界几何体上的皮肤效应(即通用皮肤效应),这依赖于一个猜想。该猜想的证明在附注1中讨论。
图2:定理证明的草图。
The first step connects the nonzero spectral area and nonzero spectral winding number along some direction in the BZ. The latter means the Hamiltonian exhibits the skin effect under the corresponding stripe geometry, which is proved in the second step. The skin effect on stripe geometry further reveals the universal skin effect, relying on a conjecture in the third step.
第一步是在布里渊区中沿某个方向连接非零谱区域和非零谱绕数。后者意味着哈密顿量在相应条纹几何下表现出皮肤效应,在第二步中得到证明。条纹几何下的皮肤效应进一步揭示了普遍的皮肤效应,这依赖于第三步的一个猜想。
The above theorem has implied the universality of skin effect in two and higher dimensions. As Ei(BZ) is the image of the d ≥ 2-dimensional torus on the complex plane, it takes fine tuning of parameters to make Ai = 0 for every i. In fact, for single-band Hamiltonian, we can prove that A = 0 if and only if , where h(k) is a Hermitian Hamiltonian and P is a complex polynomial (see Supplementary Note 1). In other words, a randomly generated non-Hermitian Hamiltonian has skin effect: the first meaning of universality. In previous studies, other types of skin effect, such as the line-skin and the high-order-skin effect, in two and higher dimensions have been proposed30,34. These types all require the open-boundary system take a special geometry (usually a rectangle) and are hence considered special and non-generic. Additionally, the number of skin modes in the universal skin effect follows a volume law, which differentiates from the higher-order-skin effect. The skin effect when Ai ≠ 0 assumes a completely generic geometry of boundary: the second meaning of universality. The third meaning of universality lies in the fact that the higher-dimensional skin effect is compatible with all point-group symmetries, i.e., the universal skin effect can appear if and only if the spectral area is nonzero, regardless of the point-group symmetry of the bulk Hamiltonian. While in one dimension, if the bulk Hamiltonian only respects, for example, the inversion symmetry, the periodic-boundary energy spectrum has an arc-form on the complex plane, which means the absence of non-Hermitian skin effect11,23. A standing wave explanation for the theorem is provided in the Supplementary Note 2.
上述定理暗示了在二维及以上维度中,皮肤效应的普遍性。由于E(BZ)是d≥2维环面在复平面上的映像,需要对参数进行精细调整才能使得对于每个i,A=0。事实上,对于单能带哈密顿量,我们可以证明当且仅当 时,A=0,其中h(k)是一个厄米哈密顿量,P是一个复多项式(见补充说明1)。换句话说,随机生成的非厄米哈密顿量 具有皮肤效应:这是普遍性的第一种意义。在先前的研究中,还提出了其他类型的皮肤效应,如线状皮肤效应和高阶皮肤效应,它们在二维及以上维度中都需要开放边界系统采用特殊的几何形状(通常是矩形),因此被认为是特殊的和非普遍的。此外,普遍皮肤效应中的皮肤模式数量遵循体积定律,这与高阶皮肤效应不同。当A≠0时的皮肤效应假设了完全普遍的边界几何形状:这是普遍性的第二种意义。 普遍性的第三个意义在于高维皮肤效应与所有点群对称性相容,即只要谱区域非零,无论体积哈密顿量的点群对称性如何,都可以出现普遍的皮肤效应。然而,在一维情况下,如果体积哈密顿量只尊重反演对称性,周期边界能谱在复平面上呈弧形,这意味着不存在非厄米皮肤效应。关于该定理的一个驻波解释在附注2中提供。
The corner-skin and the geometry-dependent-skin effect
角皮肤和几何依赖皮肤效应
While the theorem shows that the skin effect is universal, it does not specify what skin modes look like in higher dimensions. Here, we define the current functional, which partitions the universal skin effect into non-reciprocal skin effect and generalized reciprocal skin effect. Then we report the representative phenomena in these two types, i.e., the corner-skin effect (CSE) and the geometry-dependent skin effect (GDSE), respectively.
虽然定理表明了皮肤效应是普遍存在的,但它并没有指定在更高维度中皮肤模式的样子。在这里,我们定义了电流函数,将普遍的皮肤效应分为非互易皮肤效应和广义互易皮肤效应。然后我们分别报告了这两种类型中的代表性现象,即角皮肤效应(CSE)和几何相关的皮肤效应(GDSE)。
The current functional is defined as
当前的功能被定义为
under the periodic-boundary condition, where i is the energy band index and ∇α indicates the directional derivative along certain direction α in d-dimensional momentum space. Here, n(E, E*) represents a distribution function when the system reaches to a steady state and only depends explicitly on the energy of the system state17. The nonzero current functional (labeled by J ≠ 0) is defined as: ∃ α, n, Jα[n] ≠ 0; and as a complementary set, the zero current functional (labeled by J = 0) is defined as: ∀ α, n, Jα[n] = 0. By definition, the nonzero current functional and zero current functional are complete and mutually exclusive mathematically. Therefore, we can classify the universal skin effect (nonzero spectral area) into two types according to the current functional, i.e., the non-reciprocal skin effect (J ≠ 0) and generalized reciprocal skin effect (J = 0), as illustrated in Fig. 3. Note that this classification of skin effect according to the current functional is different from the classification of intrinsic point-gap topology for symmetry class11,18 (see Supplementary Note 3). The current functional is shown to vanish in two and three dimensions under point groups Ci, D2,3,4,6, C2h,3h,4h,6h, D2d,3d,2h,3h,4h,6h, T, Td,h, O and Oh. Therefore, the non-reciprocal skin effect is only compatible with point groups Cm and C2,3,4,6,2v,3v,4v,6v. As a comparison, the generalized reciprocal skin effect is compatible with all point-group symmetries (see also Supplementary Note 3).
在周期边界条件下,其中i是能带索引,∇ α 表示沿d维动量空间中某个方向α的方向导数。在这里,n(E, E * )表示系统达到稳定状态时的分布函数,仅显式依赖于系统状态的能量 17 。非零电流泛函(标记为J ≠ 0)定义为:∃ α, n, J α [n] ≠ 0;作为补充集合,零电流泛函(标记为J = 0)定义为:∀ α, n, J α [n] = 0。根据定义,非零电流泛函和零电流泛函在数学上是完备且互斥的。因此,根据电流泛函,我们可以将普遍的皮肤效应(非零谱区域)分为两种类型,即非互易皮肤效应(J ≠ 0)和广义互易皮肤效应(J = 0),如图3所示。请注意,根据电流泛函对皮肤效应进行的分类与对对称类别 11,18 的内在点-间隙拓扑的分类不同(见补充说明3)。 在C、D 2,3,4,6 、C 2h,3h,4h,6h 、D 2d,3d,2h,3h,4h,6h 、T、T d,h 、O和O h 点群下,当前的功能在二维和三维中都被证明为零。因此,非互易皮肤效应只与C m 和C 2,3,4,6,2v,3v,4v,6v 点群相容。作为对比,广义互易皮肤效应与所有点群对称性相容(另见补充说明3)。
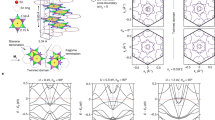
图3:角部皮肤效应和几何依赖的皮肤效应。
The universal skin effect can be further classified into two types by the current functional, that is, non-reciprocal skin effect ( ∃ α, n, Jα[n] ≠ 0) and generalized reciprocal skin effect ( ∀ α, n, Jα[n] = 0). CSE (a)–(d) and GDSE (e)-(h) are representatives of these two types of skin effects, respectively. In (a, b, e, f), the light blue regions represent the spectrum under periodic boundary, where 200*200 k-grid is used, and the red points represent the eigenvalues under different open-boundary geometries. The system size under square geometry in (c, g) is Lx × Ly = 60 × 60, and each triangle geometry in (d, h) has the same right-angled side length Lx = Ly = 60. The spatial distributions of eigenstates W(x) are plotted in (c, d, g, h) with the color bars. In the system with GDSE, the skin effect disappears under square geometry (geometry 1) in (g), and reappears under triangle geometry (geometry 2) in (h).
普遍的皮肤效应可以根据电流功能进一步分为两种类型,即非互易皮肤效应(∃α,n,J α [n] ≠ 0)和广义互易皮肤效应(∀α,n,J α [n] = 0)。CSE(a)-(d)和GDSE(e)-(h)分别代表这两种类型的皮肤效应。在(a,b,e,f)中,浅蓝色区域表示周期边界下的频谱,使用了200*200的k网格,红点表示不同开放边界几何形状下的特征值。在(c,g)中,正方形几何形状的系统尺寸为L x × L y = 60 × 60,在(d,h)中,每个三角形几何形状的直角边长相同,为L x = L y = 60。特征态W(x)的空间分布在(c,d,g,h)中用彩色条表示。在具有广义互易皮肤效应的系统中,在正方形几何形状(几何形状1)下皮肤效应消失(g),在三角形几何形状(几何形状2)下重新出现(h)。
We define the CSE as a type of the non-reciprocal skin effect (J ≠ 0) that exhibits the particular phenomenon that almost all eigenstates are localized at corners of the open-boundary geometry. The Hamiltonian of the example for CSE is
我们将CSE定义为一种非互逆的皮肤效应(J ≠ 0),它表现出几乎所有本征态都局限在开放边界几何体的角落的特殊现象。CSE的示例哈密顿量是
of which the spectral area under square geometry and triangle geometry is shown in Fig. 3(a, b) with light blue color. Because of the nonzero spectral area, the theorem tells us that the Hamiltonian must have the universal skin effect. This is verified in Fig. 3(c, d), where the spatial distributions of all eigenstates under different open boundaries are plotted. Here ψn(x) is a normalized right eigenstate and N is the number of these eigenstates. It is found that the wave functions are always localized at the corner of the boundary in Fig. 3(c), even if the open-boundary geometry is changed in Fig. 3(d). We elaborate on the localization of eigenstates for this example in the Supplementary Note 4. We also plot the corresponding eigenvalue spectra under different open boundaries, as shown in Fig. 3(a, b) with red color. One can notice that the spectral areas under periodic and open boundaries do not equal. The CSE is a representative one of non-reciprocal skin effect and inherits its features, including nonzero current functional and incompatibility with certain point-group symmetries.
其中,图3(a, b)以浅蓝色显示了正方形几何和三角形几何的光谱面积。由于非零的光谱面积,定理告诉我们哈密顿量必须具有普遍的皮肤效应。这在图3(c, d)中得到了验证,其中绘制了在不同开放边界下的所有本征态 的空间分布。这里ψ n (x)是一个归一化的右本征态,N是这些本征态的数量。发现在图3(c)中,波函数始终局限在边界的角落,即使在图3(d)中改变了开放边界的几何形状。我们在补充说明4中详细阐述了这个例子的本征态局域化。我们还绘制了在不同开放边界下的相应本征值谱,如图3(a, b)所示,以红色显示。可以注意到周期性和开放边界下的光谱面积不相等。CSE是非互易皮肤效应的代表之一,并继承了其特点,包括非零电流功能和与某些点群对称性不兼容。
Similar to the definition of CSE, the GDSE is one type of generalized reciprocal skin effect (J = 0) showing the unique phenomenon that there is at least one fully open boundary geometry under which the skin effect does not appear. The Hamiltonian of the example for GDSE reads
与CSE的定义类似,GDSE是一种广义互逆皮肤效应(J = 0),显示了至少存在一种完全开放的边界几何形状,在该形状下皮肤效应不会出现的独特现象。GDSE示例的哈密顿量如下:
Since the spectral area is nonzero, our theorem tells us that the system must have skin effect for certain open-boundary geometry, such as a random polygon. However, an interesting phenomenon in this example is that the skin effect disappears under the square geometry due to the existence of two mirror symmetries shown in Fig. 3(g). Once we choose other types of boundaries where mirror symmetries are broken, the skin effect reappears as shown in Fig. 3(h). Since the appearance of the skin effect and the localization position depend on the geometry, it is called the GDSE. In one dimension, an open chain does not exhibit skin effect when its spectrum coincides with the corresponding periodic-boundary spectrum on the complex plane. Unlike in one dimension, even if the region covered by the energy spectrum under some open-boundary geometry (such as the triangle geometry in Fig. 3(h)) seems to be the same as the region covered by the periodic-boundary spectrum, the system can still show a skin effect due to the different density of states on the complex plane. It is also a unique feature in two- and higher-dimensional skin effects. In the Supplementary Note 4, we provide some numerical results to illuminate this new type of skin effect and discuss the localization of eigenstates on the open-boundary geometry. In addition, we show that GDSE follows the volume law, i.e., the increase in the number of skin modes is proportional to the increase in the system volume. For GDSE, there is at least one spatial geometry such that skin modes vanish, and as such is mutually exclusive with CSE. Additionally, GDSE is compatible with all point groups, in contrast to CSE.
由于光谱区域非零,我们的定理告诉我们,对于某些开放边界的几何形状,比如随机多边形,系统必须具有皮肤效应。然而,在这个例子中的一个有趣现象是,由于图3(g)中显示的两个镜像对称存在,正方形几何形状下皮肤效应消失了。一旦我们选择其他类型的边界,其中镜像对称被破坏,皮肤效应就会重新出现,如图3(h)所示。由于皮肤效应的出现和局部化位置取决于几何形状,它被称为GDSE。在一维情况下,当开放链的光谱与复平面上对应的周期边界光谱重合时,它不会表现出皮肤效应。与一维情况不同的是,即使在某些开放边界几何形状下(如图3(h)中的三角形几何形状),能谱覆盖的区域似乎与周期边界光谱覆盖的区域相同,系统仍然可以显示出皮肤效应,这是由于复平面上的态密度不同。这也是二维和高维皮肤效应的独特特征。 在补充说明4中,我们提供了一些数值结果来阐明这种新型的皮肤效应,并讨论了在开放边界几何结构上的本征态的局域化。此外,我们展示了GDSE遵循体积定律,即皮肤模式数量的增加与系统体积的增加成比例。对于GDSE,至少存在一种空间几何结构使得皮肤模式消失,并且与CSE互斥。此外,与CSE不同,GDSE与所有点群都兼容。
Corollary: skin effect from exceptional points
推论:来自异常点的皮肤效应
An immediate corollary of our theorem is that all lattice Hamiltonians with stable exceptional points have universal skin effect, connecting two unique phenomena in the non-Hermitian band theory. This connection has also been discussed in ref. 31, where the bands around the stable exceptional point form a point gap with nonzero spectral winding number, consequently, exhibiting the skin effect under an open-boundary geometry. Consider a stable exceptional point k0 in two dimensions. Due to the branch point structure of exceptional point, the dispersion around k0 can be expressed as8, where qi=x,y denotes a small derivation from exceptional point in x or y direction, that is, qi = ki − k0i. Here c0, c1 are nonzero complex numbers and the stable exceptional point ensures the nonzero imaginary part of c1. Suppose the range of the expansion is r0, then it is clear that . By the theorem, the system must have universal skin effect (see Supplementary Note 5).
我们定理的一个直接推论是,所有具有稳定例外点的晶格哈密顿量都具有普适的皮肤效应,将非厄米带理论中的两个独特现象联系在一起。这种联系也在参考文献中讨论过,其中稳定例外点周围的带隙具有非零的谱绕数,因此在开边界几何下展现出皮肤效应。考虑一个二维中的稳定例外点k。由于例外点的分支点结构,k附近的色散可以表示为,其中q表示从例外点在x或y方向上的微小偏离,即q = k - k。这里c,c是非零复数,而稳定例外点确保了c的虚部非零。假设展开的范围是r,那么很明显。根据定理,系统必须具有普适的皮肤效应(见补充说明5)。
Now we use the photonic crystal model that has been experimentally realized in ref. 45 to demonstrate our corollary. The tight-binding model Hamiltonian with periodic boundary can be written as
现在我们使用在参考文献 45 中实验实现的光子晶体模型来证明我们的推论。具有周期边界条件的紧束缚模型哈密顿量可以写成
where σ = (σ0, σx, σy, σz) is a vector of the Pauli matrices and d(k) is a vector with four components, that is, . The parameters are chosen as follows, (t1, t2, t3, μ0, μz) = (0.4, − 0.1, 0.5, 1.35, − 0.02). As shown in Fig. 4(a), in the Hermitian limit, i.e. γ = 0, the system has two Dirac points along the x-axis. When external dissipation or radiational loss is added, i.e., γ ≠ 0, each Dirac point splits into two exceptional points shown in Fig. 4(b), connected by the bulk Fermi arc. According to our theorem, the system must have the universal skin effect, more precisely, the GDSE. Specifically, the skin effect disappears under square geometry but reappears under diamond geometry, which is verified in the Supplementary Note 6.
其中σ = (σ 0 , σ x , σ y , σ z )是Pauli矩阵的向量,d(k)是一个具有四个分量的向量,即 。参数选择如下,(t 1 , t 2 , t 3 , μ 0 , μ z ) = (0.4, − 0.1, 0.5, 1.35, − 0.02)。如图4(a)所示,在厄米极限下,即γ = 0,系统在x轴上有两个狄拉克点。当添加外部耗散或辐射损耗,即γ ≠ 0,每个狄拉克点分裂成两个异常点,如图4(b)所示,通过体内费米弧连接。根据我们的定理,系统必须具有普遍的皮肤效应,更准确地说,是GDSE。具体来说,在正方形几何下,皮肤效应消失,但在菱形几何下重新出现,这在补充说明6中得到验证。
图4:具有异常点的光子晶体模型和具有异常线的Weyl半金属。
Two Dirac points (a) of a two-dimensional photonic crystal model are split into four exceptional points (b) upon adding non-Hermitian term, such as radiational loss. Correspondingly, the evolution of Gaussian wave packet with initial velocity at the center of a diamond geometry for each ten time intervals is shown in (c) with γ = 0 (Hermitian) and (d) with γ = 1/4 (GDSE). Two Weyl points (e) of a three-dimensional Weyl semimetal are expanded into two exceptional rings (f) after the addition of non-Hermitian perturbations. The spatial distribution of eigenstates, i.e. W(x), is plotted in (g). The modulus square of the propagator from i to oPio(ω) and that from o to iPoi(ω), as functions of ω, are plotted with red color and dark cyan color in (h), respectively.
加入非埃尔米特项,如辐射损耗,将使二维光子晶体模型的两个Dirac点(a)分裂成四个特殊点(b)。相应地,以γ = 0(埃尔米特) (c),和γ = 1/4 (GDSE) (d)为初始速度在菱形几何中心的高斯波包演化分别为10个时间间隔。三维韦尔半金属的两个Weyl点(e)在加入非埃尔米特扰动后扩展为两个例外环(f)。在(g)中绘制了特征态的空间分布,即W(x)。在(h)中,以红色和深青色的颜色分别绘制了从i到o的传播子的模方和从o到iP的传播子的模方作为ω的函数。
So far, we have shown the features of the energy spectrum and wave function in the system with GDSE. We expect some observable phenomena from the skin effect, which motivates us to examine the dynamical properties for the photonic crystal model in Eq.(4). In order to show this, we simulate the time evolution of the wave packet starting at the center of the diamond geometry with an initial velocity perpendicular to one edge. Here the initial state is chosen to be Gaussian form , where is the normalization factor and x0 = y0 = 21 is the center coordinate of the diamond geometry. We plot the corresponding spatial distribution of normalized final states for every ten time intervals, where represents the open-boundary Hamiltonian on the diamond geometry. As shown in Fig. 4(c), in the Hermitian case, the center of the wave packets obeys the simple law of reflection: the center of the wave packet just bounces between the two edges while slowly dispersing with time. However, in the non-Hermitian case (γ = 1/4) with GDSE, after several oscillations between two edges, the wave packet makes a side jump into the upper left corner as shown in Fig. 4(d). The transverse motion of the wave packet induced by skin effect is explained in more detail in the Supplementary Note 6. This anomalous dynamical behavior is an experimental signature of GDSE.
到目前为止,我们已经展示了具有GDSE的系统中能谱和波函数的特征。我们期望从皮肤效应中观察到一些可观察的现象,这促使我们研究方程(4)中的光子晶体模型的动态特性。为了展示这一点,我们模拟了波包在钻石几何形状中心以垂直于一条边的初始速度开始的时间演化。这里选择的初始态取为高斯形式 ,其中 是归一化因子,x 0 = y 0 = 21是钻石几何形状的中心坐标。我们绘制了每十个时间间隔的归一化最终状态的空间分布,其中 表示钻石几何上的开边界哈密顿量。正如图4(c)所示,在厄米情况下,波包的中心遵循简单的反射规律:波包的中心在两个边界之间来回弹跳,同时随时间缓慢扩散。 然而,在非厄米情况下(γ = 1/4),通过GDSE,波包在两个边缘之间多次振荡后,如图4(d)所示,会侧跳到左上角。波包的横向运动由皮肤效应引起,详细解释见附注6。这种异常的动态行为是GDSE的实验特征。
We also propose the realization for CSE in a three-dimensional system with exceptional lines. Consider a Weyl semimetal with non-Hermitian term as a perturbation, of which the periodic-boundary Hamiltonian reads
我们还提出了在具有异常线的三维系统中实现CSE的方法。考虑一个具有非厄米项的Weyl半金属作为扰动,其周期边界哈密顿量如下:
where dr(k) and di(k) are vectors with four components, that is, and . The Hermitian part dr ⋅ σ is a Weyl semimetal possessing two Weyl points, the red cone at (0, 0, 0) and blue cone at (0, 0, π) shown in Fig. 4(e). Upon turning on the non-Hermitian term, the Weyl points evolve into two exceptional rings in Fig. 4(f). Consequently, the system exhibits the CSE with δ = 1/6 shown in Fig. 4(g), as a numerical verification of our corollary.
当d r (k)和d(k)是具有四个分量的向量时,即 和 。共轭部分d r ⋅ σ是一个具有两个Weyl点的Weyl半金属,红色圆锥位于(0, 0, 0),蓝色圆锥位于(0, 0, π),如图4(e)所示。打开非共轭项后,Weyl点演化为图4(f)中的两个例外环。因此,系统展示了图4(g)中δ = 1/6的CSE,作为我们推论的数值验证。
Experimentally, the non-reciprocity of the CSE can be detected by the two-point Green’s function. The modulus square of the propagator from i = (1, 1, 1) to o = (16, 16, 16) is expressed as , where α, β label the orbitals of the unit cell. We calculate Poi(ω) and Pio(ω) in Fig. 4(h), where a significant difference between them demonstrates the non-reciprocity of CSE.
实验上,可以通过两点格林函数来检测CSE的非互易性。从i = (1, 1, 1)到o = (16, 16, 16)的传播子的模方可以表示为 ,其中α,β标记了单元格的轨道。我们在图4(h)中计算了P oi (ω)和P io (ω),它们之间的显著差异表明了CSE的非互易性。
Discussion 讨论
Our work has built a bridge between two distinct phenomena that only exist in non-Hermitian systems, i.e., the exceptional points (lines) and the non-Hermitian skin effect, by establishing the correspondence between bulk (spectral area) and boundary (universal skin effect). We prove that the skin effect is universal and compatible with all point-group symmetries and time-reversal symmetry in two and higher dimensions. Due to the universality, it is expected that the skin effect is observable in a wide range of platforms, such as photonic crystals with natural radiational loss, acoustic meta-materials and circuit networks with lossy components such as resistors. Beyond these classical systems, the skin effect can also be realized in condensed matter, e.g., the heavy-fermion material with finite quasiparticle lifetime and the Weyl-exceptional-ring semimetal. The latter is realizable in Weyl semimetals made from inverting bands that have disparate effective masses, such as d- and f-bands.
我们的工作在两个仅存在于非厄米系统中的不同现象之间建立了一座桥梁,即例外点(线)和非厄米皮肤效应,通过建立体积(谱区域)和边界(通用皮肤效应)之间的对应关系。我们证明了皮肤效应是通用的,并且与所有点群对称性和时间反演对称性在二维及更高维度上兼容。由于其通用性,预计皮肤效应可以在各种平台上观察到,例如具有自然辐射损耗的光子晶体、具有损耗元件(如电阻器)的声学超材料和电路网络。除了这些经典系统外,皮肤效应还可以在凝聚态物质中实现,例如具有有限准粒子寿命的重费米子材料和韦尔-例外-环半金属。后者可以在由具有不同有效质量的反转带构成的韦尔半金属中实现,例如d-和f-带。
One should be reminded, however, that the results in this paper assume the coherent dynamics of the constituent degrees of freedom, which is unlikely the case in macroscopic condensed-matter systems where the coherence length is shorter than the system size. On the contrary, for the systems where the system size and the coherent length are comparable, as in mesoscopic systems, we believe that the universal skin effect has a significant contribution to the transport properties, a subject for future exploration.
然而,需要提醒的是,本文的结果假设组成自由度的相干动力学,而在宏观凝聚态系统中,相干长度较系统尺寸短的情况是不太可能的。相反,对于系统尺寸和相干长度相当的介观系统,我们相信普适的皮肤效应对输运性质有重要贡献,这是一个需要进一步探索的课题。
Data availability 数据可用性
Raw numerical data from the plots presented are available from the authors upon request.
请向作者请求获取所呈现的图表的原始数值数据。
Code availability 代码可用性
The code used to generate the figures are available from the authors upon reasonable request.
生成图表所使用的代码可在合理请求下向作者获取。
References 参考资料
Gamow, G. Zur Quantentheorie des Atomkernes. Z. f.ür. Phys. 51, 204–212 (1928).
Gamow,G.关于原子核的量子理论。Z. f.ür. Phys. 51,204-212(1928)。Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
小泽等人。拓扑光子学。《物理评论快报》91,015006(2019)。Feng, L., El-Ganainy, R. & Ge, L. Non-Hermitian photonics based on parity-time symmetry. Nat. Photonics 11, 752–762 (2017).
冯,L.,El-Ganainy,R.和Ge,L.基于偶-奇时间对称性的非厄米光子学。自然光子学,11,752-762(2017年)。El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. Nat. Phys. 14, 11–19 (2018).
El-Ganainy, R.等。非厄米物理和PT对称性。自然物理学。14, 11-19 (2018)。Kozii, V. & Fu, L. Non-Hermitian topological theory of finite-lifetime quasiparticles: prediction of bulk fermi arc due to exceptional point. arXiv:1708.05841 (2017).
Nagai, Y., Qi, Y., Isobe, H., Kozii, V. & Fu, L. DMFT reveals the non-hermitian topology and fermi arcs in heavy-fermion systems. Phys. Rev. Lett. 125, 227204 (2020).
Leykam, D., Bliokh, K. Y., Huang, C., Chong, Y. D. & Nori, F. Edge modes, degeneracies, and topological numbers in non-hermitian systems. Phys. Rev. Lett. 118, 040401 (2017).
Shen, H., Zhen, B. & Fu, L. Topological band theory for Non-Hermitian Hamiltonians. Phys. Rev. Lett. 120, 146402 (2018).
Gong, Z. et al. Topological phases of Non-Hermitian systems. Phys. Rev. X 8, 031079 (2018).
Bergholtz, E. J., Budich, J. C. & Kunst, F. K. Exceptional topology of non-Hermitian systems. Rev. Mod. Phys. 93, 015005 (2021).
Kawabata, K., Shiozaki, K., Ueda, M. & Sato, M. Symmetry and topology in Non-Hermitian physics. Phys. Rev. X 9, 041015 (2019).
Ashida, Y., Gong, Z. & Ueda, M. Non-hermitian physics. Adv. Phys. 69, 249–435 (2020).
Yao, S. & Wang, Z. Edge states and topological invariants of Non-Hermitian systems. Phys. Rev. Lett. 121, 086803 (2018).
Yao, S., Song, F. & Wang, Z. Non-Hermitian chern bands. Phys. Rev. Lett. 121, 136802 (2018).
Kunst, F. K., Edvardsson, E., Budich, J. C. & Bergholtz, E. J. Biorthogonal bulk-boundary correspondence in Non-Hermitian systems. Phys. Rev. Lett. 121, 026808 (2018).
Yokomizo, K. & Murakami, S. Non-Bloch band theory of Non-Hermitian systems. Phys. Rev. Lett. 123, 066404 (2019).
Zhang, K., Yang, Z. & Fang, C. Correspondence between winding numbers and skin modes in Non-Hermitian systems. Phys. Rev. Lett. 125, 126402 (2020).
Okuma, N., Kawabata, K., Shiozaki, K. & Sato, M. Topological origin of Non-Hermitian skin effects. Phys. Rev. Lett. 124, 086801 (2020).
Yang, Z., Zhang, K., Fang, C. & Hu, J. Non-Hermitian bulk-boundary correspondence and auxiliary generalized brillouin zone theory. Phys. Rev. Lett. 125, 226402 (2020).
Martinez Alvarez, V. M., Barrios Vargas, J. E. & Foa Torres, L. E. F. Non-Hermitian robust edge states in one dimension: Anomalous localization and eigenspace condensation at exceptional points. Phys. Rev. B 97, 121401(R) (2018).
Lee, C. H. & Thomale, R. Anatomy of skin modes and topology in non-Hermitian systems. Phys. Rev. B 99, 201103(R) (2019).
Kawabata, K., Okuma, N. & Sato, M. Non-Bloch band theory of non-Hermitian Hamiltonians in the symplectic class. Phys. Rev. B 101, 195147 (2020).
Yi, Y. & Yang, Z. Non-Hermitian Skin Modes Induced by On-Site Dissipations and Chiral Tunneling Effect. Phys. Rev. Lett. 125, 186802 (2020).
Xiong, Y. Why does bulk boundary correspondence fail in some non-hermitian topological models. J. Phys. Commun. 2, 035043 (2018).
Yang, Z. Non-perturbative Breakdown of Bloch’s Theorem and Hermitian Skin Effects. arXiv:2012.03333 (2020).
Ashcroft, N. W. & Mermin, N. D.Solid State Physics (Holt-Saunders, 1976).
Xiao, L. et al. Non-Hermitian bulk–boundary correspondence in quantum dynamics. Nat. Phys. 16, 761–766 (2020).
Ghatak, A., Brandenbourger, M., van Wezel, J. & Coulais, C. Observation of non-Hermitian topology and its bulk-edge correspondence in an active mechanical metamaterial. Proc. Natl. Acad. Sci. 117, 29561–29568 (2020).
Helbig, T. et al. Generalized bulk–boundary correspondence in non-Hermitian topolectrical circuits. Nat. Phys. 16, 747–750 (2020).
Lee, C. H., Li, L. & Gong, J. Hybrid Higher-Order Skin-Topological Modes in Nonreciprocal Systems. Phys. Rev. Lett. 123, 016805 (2019).
Hofmann, T. et al. Reciprocal skin effect and its realization in a topolectrical circuit. Phys. Rev. Res. 2, 023265 (2020).
Yoshida, T., Mizoguchi, T. & Hatsugai, Y. Mirror skin effect and its electric circuit simulation. Phys. Rev. Res. 2, 022062(R) (2020).
Liu, T. et al. Second-order topological phases in Non-Hermitian systems. Phys. Rev. Lett. 122, 076801 (2019).
Kawabata, K., Sato, M. & Shiozaki, K. Higher-order non-Hermitian skin effect. Phys. Rev. B 102, 205118 (2020).
Scheibner, C., Irvine, W. T. M. & Vitelli, V. Non-Hermitian band topology and skin modes in active elastic media. Phys. Rev. Lett. 125, 118001 (2020).
Li, L., Lee, C. H. & Gong, J. Topological switch for Non-Hermitian skin effect in cold-atom systems with loss. Phys. Rev. Lett. 124, 250402 (2020).
Song, F., Wang, H.-Y. & Wang, Z. Non-Bloch PT symmetry breaking: Universal threshold and dimensional surprise. arXiv:2102.02230 (2021).
Lin, Z. et al. Unidirectional invisibility induced by -symmetric periodic structures. Phys. Rev. Lett. 106, 213901 (2011).
Miri, M.-A. & Alù, A. Exceptional points in optics and photonics. Science 363, eaar7709 (2019).
Özdemir, Ş. K., Rotter, S., Nori, F. & Yang, L. Parity–time symmetry and exceptional points in photonics. Nat. Mater. 18, 783–798 (2019).
Kawabata, K., Bessho, T. & Sato, M. Classification of exceptional points and non-hermitian topological semimetals. Phys. Rev. Lett. 123, 066405 (2019).
Yang, Z., Chiu, C.-K., Fang, C. & Hu, J. Jones polynomial and knot transitions in hermitian and non-hermitian topological semimetals. Phys. Rev. Lett. 124, 186402 (2020).
Yang, Z., Schnyder, A. P., Hu, J. & Chiu, C.-K. Fermion doubling theorems in two-dimensional Non-Hermitian systems for fermi points and exceptional points. Phys. Rev. Lett. 126, 086401 (2021).
Zhen, B. et al. Spawning rings of exceptional points out of Dirac cones. Nature 525, 354–358 (2015).
Zhou, H. et al. Observation of bulk Fermi arc and polarization half charge from paired exceptional points. Science 359, 1009–1012 (2018).
Cerjan, A. et al. Experimental realization of a Weyl exceptional ring. Nat. Photonics 13, 623–628 (2019).
Tang, W. et al. Exceptional nexus with a hybrid topological invariant. Science 370, 1077–1080 (2020).
Dembowski, C. et al. Experimental observation of the topological structure of exceptional points. Phys. Rev. Lett. 86, 787–790 (2001).
Regensburger, A. et al. Parity–time synthetic photonic lattices. Nature 488, 167–171 (2012).
Gao, T. et al. Observation of non-Hermitian degeneracies in a chaotic exciton-polariton billiard. Nature 526, 554–558 (2015).
Doppler, J. et al. Dynamically encircling an exceptional point for asymmetric mode switching. Nature 537, 76–79 (2016).
Hodaei, H. et al. Enhanced sensitivity at higher-order exceptional points. Nature 548, 187–191 (2017).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Acknowledgements
C.F. acknowledges funding support by the Ministry of Science and Technology of China under grant number 2016YFA0302400, and the Chinese Academy of Sciences under grant number XDB33000000. Z.Y. acknowledges funding support by the National Science Foundation of China (Grant No. NSFC-12104450) and the fellowship of China National Postdoctoral Program for Innovative Talents (Grant No. BX2021300).
Author information
Authors and Affiliations
Contributions
C.F. conceived the work; K.Z. did the major part of the theoretical derivation and numerical calculation; Z.Y. wrote and analyzed the tight-binding Hamiltonian of the photonic crystal model; All authors discussed the results and participated in the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, K., Yang, Z. & Fang, C. Universal non-Hermitian skin effect in two and higher dimensions. Nat Commun 13, 2496 (2022). https://doi.org/10.1038/s41467-022-30161-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-30161-6
This article is cited by
-
Observation of continuum Landau modes in non-Hermitian electric circuits
Nature Communications (2024)
-
Detecting bulk and edge exceptional points in non-Hermitian systems through generalized Petermann factors
Frontiers of Physics (2024)
-
Non-Hermitian reconstruction of photonic hierarchical topological states
Communications Physics (2023)
-
Terminal-coupling induced critical eigenspectrum transition in closed non-Hermitian loops
Scientific Reports (2023)
-
Multi-dimensional band structure spectroscopy in the synthetic frequency dimension
Light: Science & Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.