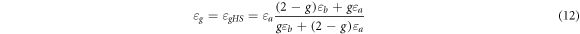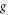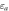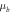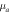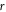Abstract 摘要
A novel closed-form expression for predicting the equivalent electromagnetic parameters of the honeycomb structure is proposed. It is obtained by approximating the correlation terms in the derivation of the strong fluctuation theory with the integral of the spherically symmetric function. Through several simulation examples, the calculation results of the formula are compared with the results of several traditional extraction methods and compared with the existing experimental data. Comparison of the extraction results of the formula with the simulation results and the experimental data shows good agreement, which proves the feasibility of the extraction expression, and this method does not require simulation as a prerequisite and can shorten the time for optimizing the design of the honeycomb absorbing structure.
提出了一种预测蜂窝结构等效电磁参数的新型闭式表达式。它是通过用球面对称函数积分近似推导强波动理论中的相关项得到的。通过几个仿真实例,将公式的计算结果与几种传统提取方法的结果进行了比较,并与现有的实验数据进行了对比。公式的提取结果与仿真结果和实验数据的比较显示出良好的一致性,这证明了提取表达式的可行性,而且这种方法不需要仿真作为前提条件,可以缩短优化蜂窝吸波结构设计的时间。
Export citation and abstract
BibTeX
RIS
导出引文和摘要 BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
本作品的原创内容可根据创作共用署名 4.0 许可证的条款使用。对本作品的任何进一步传播都必须注明作者、作品名称、期刊引文和 DOI。
1. Introduction 1.导言
Radar absorbing structure is widely used in civil and military fields, and honeycomb structure composite materials have become one of the important research directions of radar absorbing structure due to their excellent mechanical load-bearing characteristics and electromagnetic properties, which hexagonal structure is the most common form of the honeycomb structure and is most widely used [1, 2]. When the size of the mixture is much smaller than the wavelength of the el-ectromagnetic wave, homogenization is an effective method to treat the electromagnetic characteristics of the mixture equivalently [3]. In the past few decades, many equivalent electromagnetic parameter prediction theories have been proposed by researchers. Such as Bruggeman theory [4], HS theory(HS) [5] and strong fluctuation theory(SFT) [6].There are many optimal designs of honeycomb absorbing structures, which use the HS theory(HS) to extract the equivalent parameters of each phase material in the structure [7–11].
雷达吸波结构广泛应用于民用和军用领域,蜂窝结构复合材料以其优异的力学承载特性和电磁特性成为雷达吸波结构的重要研究方向之一,其中六边形结构是最常见的蜂窝结构形式,应用最为广泛[1、2]。当混合物的尺寸远小于电磁波的波长时,均质化是等效处理混合物电磁特性的有效方法[3]。在过去的几十年中,研究人员提出了许多等效电磁参数预测理论。如 Bruggeman 理论 [4]、HS 理论(HS)[5] 和强波动理论(SFT)[6]。有许多蜂窝吸波结构的优化设计都是利用 HS 理论(HS)提取结构中各相材料的等效参数[7-11] 。
Although we can forward calculate the equivalent parameters by the expressions derived from strong fluctuation theory (SFT). Usually, the effect of correlation terms is ignored when the equivalent parameters are extracted by strong fluctuation theory(SFT), whereas Tsang and Kong considered that by gave several specific correlation functions and their integration, and calculated the equivalent dielectric constant of the mixtures of the two constituents and three constituents [12]. In the process of deriving the strong fluctuation theory, Zhao [13] used polynomial expansion to approximate the correlation terms, and obtained the coefficients of each term of the polynomial by algorithm fitting [14], and obtained the closed-form expressions for calculating the equivalent electromagnetic parameters. The more the polynomial expansion terms are, the more accurate the extraction result is. However, this method needs to get S-parameters through simulation first, which reduces the universality of the method. Zhu and Tan [15, 16] use the bicontinuous media generated by Gaussian random process to represent snow, and use the strong fluctuation theory to obtain the analytical solution of the effective permittivity of snow. The accuracy of the extraction results are good in X-band.
虽然我们可以通过强波动理论(SFT)推导出的表达式来正向计算等效参数。通常情况下,强波动理论(SFT)提取等效参数时忽略了相关项的影响,而 Tsang 和 Kong 考虑到了这一点,给出了几个特定的相关函数及其积分,计算出了两种成分和三种成分混合物的等效介电常数[12]。在推导强波动理论的过程中,赵国栋[13]利用多项式展开逼近相关项,并通过算法拟合得到多项式各项式系数[14],得到了计算等效电磁参数的闭式表达式。多项式展开项越多,提取结果越精确。然而,这种方法需要先通过仿真得到 S 参数,降低了方法的普适性。Zhu 和 Tan [15, 16] 用高斯随机过程产生的双连续介质表示雪,利用强波动理论得到雪的有效介电常数解析解。在 X 波段的提取结果精度较好。
Therefore, this paper makes an effort to make the prediction of the the equivalent parameters of honeycomb structure have dispersion characteristics and more accurate. A closed- form expression for the extraction of equivalent parameters is obtained by approximating the correlation terms with the integral of the spherically symmetric function in the derivation of the strong fluctuation theory. After that, by giving several simulation examples of honeycomb structure, the calculation results of the closed-form expressions are compared with the extraction results of the HS theory (HS) and strong fluctuation theory(SFT), and the correctness of the expressions are preliminarily verified. In order to further verify the correctness of the expressions, the extraction results of the expressions are compared with the existing experimental data. The comparison results show that this method has good accuracy, and provides a time-saving, forward and feasible method for the extraction of equivalent parameters.
因此,本文致力于使具有分散特性的蜂窝结构等效参数的预测更加准确。在强波动理论的推导过程中,通过用球面对称函数积分逼近相关项,得到了提取等效参数的闭式表达式。然后,通过给出几个蜂窝结构的仿真实例,将闭式表达式的计算结果与 HS 理论(HS)和强波动理论(SFT)的提取结果进行比较,初步验证了表达式的正确性。为了进一步验证表达式的正确性,将表达式的提取结果与现有的实验数据进行了比较。对比结果表明,该方法具有良好的准确性,为等效参数的提取提供了一种省时、前瞻、可行的方法。
2. Closed-form expression for extraction of equivalent electromagnetic parameters
2.提取等效电磁参数的闭式表达式
The honeycomb structure is considered to be a symmetrical structure in cross-section, and its schematic diagram is shown in figure 1. the honeycomb structure is composed of the host material and the filling material which is homogeneous and isotropic and with permittivities
蜂窝结构被认为是一种横截面对称的结构,其示意图如图1所示。蜂窝结构由主材料和填充材料组成,主材料和填充材料是均匀的、各向同性的,其介电常数
Figure 1. Cross-section diagram of honeycomb.
图 1.蜂巢截面图。
Download figure: 下载图表
Standard image High-resolution image标准图像 高分辨率图像。
Considering the normal incident wave, in the low frequency limit, the radial effective permittivity of honeycomb structure is [6]
考虑到法向入射波,在低频极限,蜂窝结构的径向有效介电常数为 [6] 。
Where according to the homogenization method, honeycomb structure acts as an uniaxially but homogeneous material with diagonal effective permittivity tensor. Considering the effective permittivity of the X direction
根据均质化方法,蜂窝结构是一种单轴均质材料,其有效介电常数张量为对角线。考虑到 X 方向
and
和
For uniaxial media, the dyadic Green's function can be decomposed into a principal value part with excluded volume and a delta function [17, 18]
对于单轴介质,二元格林函数可分解为具有排除体积的主值部分和三角函数 [17, 18] 。
Where
其中
So the
因此,(1) 的
Where
其中,
To get the direct calculation formula, the spherically symmetric correlation function is used to approximate the
为了得到直接计算公式,使用球形对称相关函数来近似
Where
其中,
In this case, the formula (6) can be changed to [12]
在这种情况下,公式 (6) 可以改为 [12] 。
Where
其中
Substituting
将
Where
其中,
Where
其中,
From above the closed-form expression for radial effective permittivity
由上可知,
Where
其中
Because the accuracy of extraction results of HS upper bound is better than that of the strong fluctuation theory at low frequency,
因为在低频时,HS 上界提取结果的准确性优于强波动理论、
Where
其中
3. Results and discussion
3.结果和讨论
Several numerical simulation examples are given to verify the extraction results of the closed-form expression of the effective permittivity in the previous part. Figure 2 compares the real part and imaginary part of effective permittivity obtained by several different methods. The permittivities and permeabilities of host and filling materials are set to
本文给出了几个数值模拟实例,以验证上一部分中有效介电常数闭式表达式的提取结果。图 2 比较了几种不同方法得到的有效介电常数的实部和虚部。主材料和填充材料的介电常数和渗透率设置为
Figure 2. Comparison between simulation results and prediction resul-ts: (a) real part of
图 2。 模拟结果与预测结果的比较:(a) 的实部
Download figure: 下载图表
Standard image High-resolution image标准图像 高分辨率图像。
In figure 2, the dotted line is the value extracted by retrieval method (NRW) [19, 20] and the accuracy of HS upper bound [8] extraction results are better than SFT [13] extraction result in the whole frequency band, so it is reasonable to take HS upper extraction results as the initial value of the formula. However, the extraction results of HS and SFT are not dispersive. The extraction results of closed-form expression reflect the dispersion characteristics very well and have good accuracy in 2–18 GHz, However, with the increase of honeycomb mesh size, the influence of higher order mode increases gradually and the accuracy of extraction results will gradually decrease.
在图2中,虚线为检索方法(NRW)提取的值[19、20] 和 HS 上限 [8] 提取结果的准确性在整个频段都优于 SFT [13] 提取结果,因此将 HS 上限提取结果作为公式的初始值是合理的。然而,HS 和 SFT 的提取结果并不分散。闭式表达式的提取结果很好地反映了频散特性,在 2-18 GHz 频段具有较好的精度,但随着蜂窝网格尺寸的增大,高阶模的影响逐渐增大,提取结果的精度会逐渐降低。
To further make the formula more convincing, the extraction results are compared with the experimental data in the existing literature [8]. The aperture size
为了使公式更有说服力,我们将提取结果与现有文献 [8] 中的实验数据进行了比较。蜂窝的孔径大小
Figure 3 shows the comparison results between the simulated reflectivity and the actually measured reflectivity. At low frequency, the simulation results are basically consistent with the experimental data. With the increase of frequency, the reflection coefficient at the resonance point of the simulated reflectivity is always smaller than the actual value. This is because of high frequency, the predicted value of the imaginary part of the permittivity is slightly larger than the actual value, which leads to the increase of material loss and enhancement of the absorbing effect.
图 3 显示了模拟反射率与实际测量反射率的比较结果。在低频时,模拟结果与实验数据基本一致。随着频率的增加,模拟反射率在共振点的反射系数总是小于实际值。这是因为在高频情况下,介电常数虚部的预测值略大于实际值,从而导致材料损耗增加,吸波效果增强。
Figure 3. Reflectivity of measured results and simulation results.
图 3.测量结果和模拟结果的反射率。
Download figure: 下载图表
Standard image High-resolution image标准图像 高分辨率图像。
4. Conclusion 4.结论
A closed-form expression for calculating the effective permittivities of the honeycomb structure is obtained by approximating the correlation terms with the integral of the spherically symmetric function in this paper, and compared it with the simulation results and the existing experimental data. It proved that the extraction formula of the effective permittivities was correct. In the frequency range studied, the extraction results of the real part of the effective permittivities are consistent with the experimental data, and the imaginary part has a good agreement in the low frequency band. So the spherically symmetric correlation function can basically express the interaction relationship of each component material in the honeycomb structure. Using the closed-form expression to calculate the equivalent electromagnetic parameters of honeycomb structure can be used for the design of honeycomb absorbing structure and shorten its time.
本文通过用球面对称函数的积分逼近相关项,得到了计算蜂窝结构有效介电常数的闭式表达式,并将其与模拟结果和现有实验数据进行了比较。结果证明,有效容限的提取公式是正确的。在所研究的频率范围内,有效容限实部的提取结果与实验数据一致,虚部在低频段也有很好的一致性。因此,球对称相关函数基本上可以表达蜂窝结构中各组成材料的相互作用关系。利用该闭式表达式计算蜂窝结构的等效电磁参数可用于蜂窝吸波结构的设计,缩短设计时间。
Data availability statement
数据可用性声明
The data generated and/or analysed during the current study are not publicly available for legal/ethical reasons but are available from the corresponding author on reasonable request.
出于法律/道德原因,本研究中生成和/或分析的数据不对外公开,但可向通讯作者索取。
We are sorry, but references for this article are not available right now.
Please try again later.
很抱歉,现在还没有这篇文章的参考资料。请稍后再试。








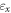




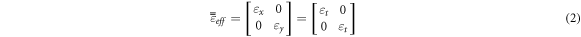







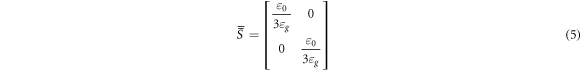






![${[]}_{mn}$](https://content.cld.iop.org/journals/2053-1591/8/8/085801/revision2/mrxac1ac5ieqn21.gif)






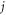
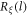

![${[{\overline{\overline{\delta }}}_{\xi }]}_{mn}$](https://content.cld.iop.org/journals/2053-1591/8/8/085801/revision2/mrxac1ac5ieqn28.gif)