The strongest force in the universe is called, aptly, the strong force. We never get to witness its fearsome power because it works only across subatomic distances, where it binds quarks together inside protons and neutrons and joins those nucleons into atomic nuclei. Of the four basic forces of nature, the strong force is by far the most potent—it’s 100 trillion trillion trillion times stronger than the force of gravity. It’s also the most mysterious.
宇宙中最强大的力量被称作强力,非常贴切。我们从未亲眼目睹过它的可怕力量,因为它只在亚原子距离内起作用,它把质子和中子内部的夸克结合在一起,并把这些核子连接成原子核。在自然界的四种基本力量中,强力是迄今为止最强大的力量--它比万有引力强大 100 万亿万亿倍。它也是最神秘的力量。
Despite knowing roughly how it compares with the other forces, scientists don’t know precisely how strong the strong force is. The other three forces—gravity, the electromagnetic force and the weak nuclear force (responsible for some radioactivity)—are much better measured. The strength of electromagnetism, for example, denoted by its “coupling constant,” has been measured with the same precision as the distance between New York and Los Angeles, to within a few hair breadths. Yet the strong force’s coupling constant, called αs (“alpha s”), is by far the least understood of these quantities. The precision of the best measurements of αs is 100 million times worse than that of the electromagnetic measurement.
尽管科学家们大致知道强力与其他力的比较,但他们并不知道强力到底有多强。其他三种力--万有引力、电磁力和弱核力(造成某些放射性)--的测量结果要好得多。例如,电磁力的强度用 "耦合常数 "表示,其测量精度与纽约和洛杉矶之间的距离相同,都在几根头发的宽度之内。然而,强力的耦合常数α s ("α s")是迄今为止这些量中最不为人所知的。α s 的最佳测量精度比电磁测量精度差一亿倍。
Even this level of (un)certainty is known only in the simplest domain of the strong force theory, at very high energies involved only in some of the rarest and most extreme events in nature. At the lower energies relevant to the world around us, the strong force earns its name by becoming truly intense, and concrete information on αs in this range is scarce. Until recently, no one had made any experimental measurements of αs at this scale. Theoretical predictions for its value were unhelpful, covering the entire span from zero to infinity.
即使是这种程度的(不)确定性,也只是在强力理论的最简单领域,在非常高的能量下,只涉及自然界中一些最罕见和最极端的事件。在与我们周围世界相关的较低能量下,强力因其真正的强度而得名,而在这一范围内有关 α s 的具体信息却非常稀少。直到最近,还没有人在这个尺度上对α s 进行过任何实验测量。对其值的理论预测也毫无帮助,因为它涵盖了从零到无穷大的整个范围。
On supporting science journalism
关于支持科学新闻
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
如果您喜欢这篇文章,请考虑订阅以支持我们屡获殊荣的新闻报道。通过订阅,您将帮助我们确保未来能够继续报道有关塑造当今世界的发现和思想的有影响力的故事。
Jen Christiansen 詹-克里斯蒂安森
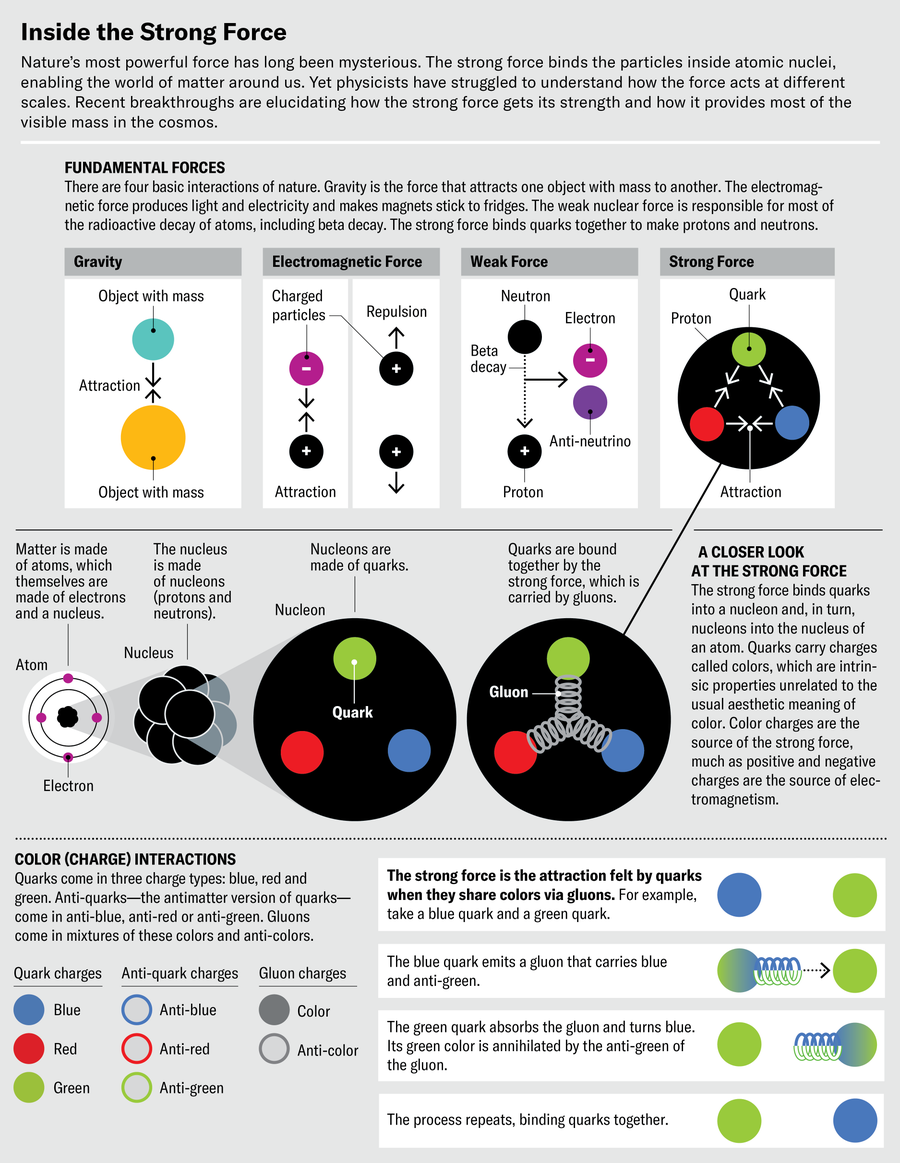
The strong force’s might makes it difficult to study in lots of ways. The theory describing how it works, called quantum chromodynamics, is so complicated we can’t use it to make direct calculations or precise predictions. One of the reasons for this complexity is that the carrier of the strong force—a particle called the gluon—interacts with itself. Electromagnetism, in comparison, is simple because its carrier, the photon, is chargeless. But the gluon carries the strong force’s version of charge, called color, and its self-interactions quickly get out of hand. So despite its importance to nuclear physics and building the material world, the strong force is not unconditionally loved by researchers. Instead many look at the domain where the strong force is truly strong as a “Terra Damnata,” a realm to avoid at all costs.
强力的强大使它在很多方面都难以研究。描述其工作原理的理论,即量子色动力学,非常复杂,我们无法用它来进行直接计算或精确预测。造成这种复杂性的原因之一是,强力的载体--一种叫做胶子的粒子--会与自身发生相互作用。相比之下,电磁学很简单,因为它的载体--光子--是不带电的。但胶子携带着强力的 "电荷"--颜色,它的自我相互作用很快就会失控。因此,尽管强力对核物理和物质世界的构建非常重要,但它并没有无条件地受到研究人员的喜爱。相反,许多人将强力真正强大的领域视为 "Terra Damnata",一个不惜一切代价也要避开的领域。
Yet understanding the strong force is essential for explaining the complexity of the matter around us. In fact, the strong force accounts for the origin of around 99 percent of the mass in the visible universe. (The remaining 1 percent comes from the Higgs boson.) And now, after half a century of effort, scientists have finally begun revealing some of the strong force’s secrets. One of us (Deur) recently made the first measurements of how αs changes within Terra Damnata, and two of us (Brodsky and Roberts) independently developed new theoretical predictions that explained the data. Terra Damnata is looking more welcoming than ever before. And now that we can explore this terrain, we stand to learn much more. We at last have the ability to analytically calculate aspects of quantum chromodynamics from first principles. Furthermore, exploring this range of the strong force could help us understand proposed unifying theories of the universe, as well as the question of how many dimensions exist in space and time.
然而,了解强力对于解释我们周围物质的复杂性至关重要。事实上,强力是可见宇宙中约 99% 的质量的来源(其余的 1% 来自希格斯玻色子)。(现在,经过半个世纪的努力,科学家们终于开始揭示强力的一些秘密。我们中的一个人(迪尔)最近首次测量了 α s 在 Damnata Terra 中的变化情况,我们中的两个人(布罗茨基和罗伯茨)独立提出了解释这些数据的新理论预测。Damnata Terra 看起来比以往任何时候都更受欢迎。既然我们能够探索这片土地,我们就能学到更多。我们终于有能力从第一原理出发,分析计算量子色动力学的各个方面。此外,探索强力的这个范围可以帮助我们理解拟议中的宇宙统一理论,以及空间和时间存在多少维度的问题。

Magnets direct particles through the Continuous Electron Beam Accelerator Facility (CEBAF) at the Thomas Jefferson National Accelerator Facility.
Courtesy of Jefferson Lab
磁铁引导粒子通过托马斯-杰斐逊国家加速器设施的连续电子束加速器(CEBAF)。
If αs is a constant, how can it change? The answer has to do with the concept of quantum loops, also known as vacuum polarization. Quantum theory revealed that the “vacuum” of space is actually full of tiny particles that are constantly appearing and disappearing in fluctuating clouds. Interactions with these virtual particles can cause a force to depart from its classical behavior because of what’s called a quantum loop. When the notion was first introduced, quantum loops were an unpleasant surprise because they predict infinite quantities—a clear sign that something is wrong. But eventually physicists figured out how to tame these infinities and absorb all the corrections from quantum loops into the equation describing the carrier of the force. Thus, in quantum chromodynamics (QCD), quantum loop corrections affect the gluon’s behavior and determine how much αs changes with the distance between quarks. With this new distance dependence from quantum loops lodged within the coupling constant, these quantities lost their constancy. So we’ll just call them “couplings” from now on.
如果 α s 是一个常数,它怎么会变化呢?答案与量子环的概念有关,也称为真空极化。量子理论揭示了空间的 "真空 "实际上充满了微小的粒子,它们在波动的云中不断出现和消失。与这些虚拟粒子的相互作用会导致力偏离其经典行为,这就是所谓的量子环。量子回路的概念刚被提出时,是一个令人不快的惊喜,因为它预示着无限的量--这显然是出了问题的迹象。但物理学家最终想出了如何驯服这些无穷量,并将量子环路的所有修正吸收到描述力的载体的方程中。因此,在量子色动力学(QCD)中,量子环修正会影响胶子的行为,并决定 α s 随夸克间距离的变化程度。由于耦合常数中新加入了量子环的距离依赖性,这些量失去了恒定性。因此,从现在起我们就称它们为 "耦合"。
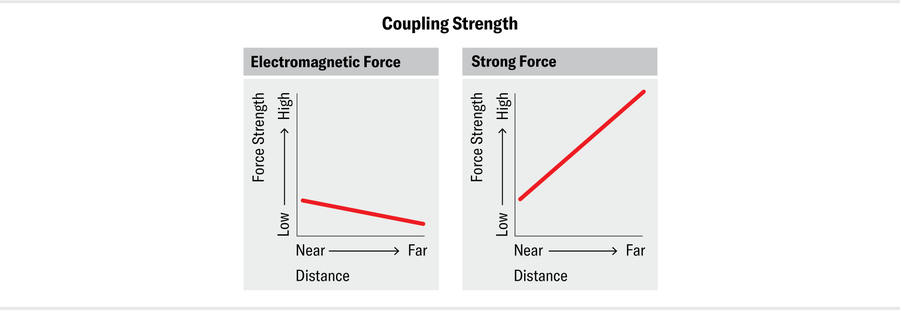
For most of the forces, the couplings change slowly with distance. For instance, from the tiniest scales ever probed by humans to everyday scales, αem, the electromagnetic coupling, decreases only by about 10 percent of its value. For the strong coupling, αs, however, the change is huge: even within the domain where physicists are comfortable calculating αs (that is, far from Terra Damnata), its value changes by several orders of magnitude. Another difference, far more important, is that the electromagnetic coupling decreases as the distance grows. For the strong force, however, αs increases with distance. If you try to pull two quarks within a proton apart from each other, the attraction between them becomes stronger. In fact, it grows so powerfully that it’s essentially impossible to pry quarks away from each other—the strong force keeps them “confined,” and you can never find a single quark by itself. The same rule applies to interactions between quarks and gluons and between gluons and gluons. The flip side is that these interactions are weak at short distances: the closer you zoom in on a quark, the more loosely it’s bound. The smallness of αs at small distances is called asymptotic freedom, and its discovery in the 1970s eventually won its pioneers the 2004 Nobel Prize in Physics.
对于大多数力来说,耦合随距离的变化而缓慢。例如,从人类探测到的最微小尺度到日常尺度,电磁耦合 α em 只减少了其值的 10%左右。然而,强耦合 α s 的变化则是巨大的:即使在物理学家能够轻松计算 α s 的领域内(即远离 Damnata 地球),其数值也会发生几个数量级的变化。另一个更为重要的区别是,电磁耦合会随着距离的增加而减小。然而,对于强力来说,α s 会随着距离的增加而增大。如果你试图把质子内的两个夸克拉开,它们之间的吸引力就会变得更强。事实上,这种吸引力会变得如此强大,以至于基本上不可能将夸克拉开--强力将它们 "禁锢 "起来,你永远找不到一个单独的夸克。同样的规则也适用于夸克和胶子之间以及胶子和胶子之间的相互作用。反过来说,这些相互作用在短距离内是微弱的:你越靠近一个夸克,它受到的束缚就越松散。α s 在小距离上的微弱作用被称为渐近自由,它在 20 世纪 70 年代的发现最终为其先驱者赢得了 2004 年诺贝尔物理学奖。
Jen Christiansen 詹-克里斯蒂安森
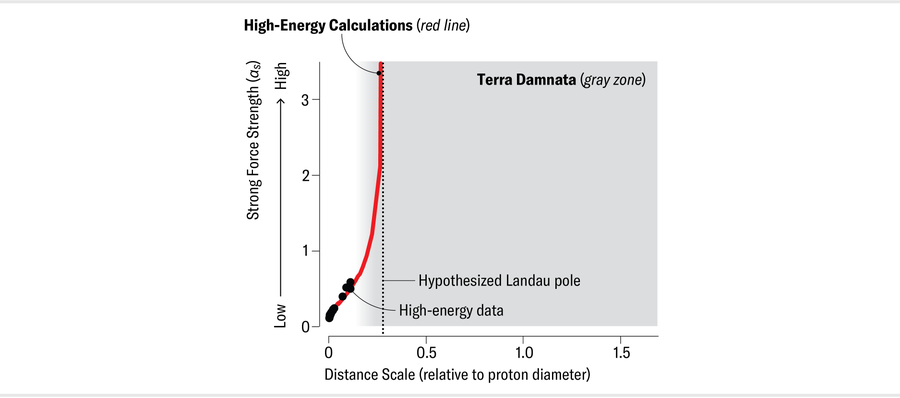
At short distances, where αs is small, physicists can perform calculations using the same methods that we use for the electromagnetic and weak forces. But these methods don’t work for QCD at longer distances—say, the size of a proton. This length is, by everyday standards, still very small (the proton, being one-50,000th the size of an atom, has a radius of roughly a millionth of a billionth of a meter). Yet it represents an expanse in particle physics. The problem is that αs grows too quickly. Before we can reach a fermi, αs becomes too big for the standard calculation method to be applicable. This is why the (not even very) long-distance domain became Terra Damnata.
在α s 较小的短距离内,物理学家可以使用与电磁力和弱力相同的方法进行计算。但在较远距离--比如质子的大小--的QCD中,这些方法就不起作用了。按照日常标准,这个长度仍然非常小(质子的大小是原子的五万分之一,半径大约是十亿分之一米的百万分之一)。然而,它却代表了粒子物理学的广阔前景。问题在于 α s 生长得太快。在我们到达费米之前,α s 就变得太大了,标准计算方法无法适用。这就是为什么(甚至不是很大的)长距离域成为 Terra Damnata 的原因。
Jen Christiansen 詹-克里斯蒂安森
With the usual calculation method unavailable, physicists tried other strategies, but they were either less well tested or imprecise and predicted a long-distance limit for αs that could lie anywhere between zero and infinity. The usual short-distance calculation method predicts an infinite value of αs at long range. But this infinity, referred to as the Landau pole after physicist Lev Landau, reveals only that the computational method has failed rather than telling us about the strong force. It was crucial to determine what αs does at a distance.
由于无法使用通常的计算方法,物理学家们尝试了其他策略,但这些策略要么没有得到很好的验证,要么不精确,而且预测α s 的远距离极限可能介于零和无穷大之间。通常的短距离计算方法预测远距离 α s 的值为无穷大。但是,这个以物理学家列夫-朗道(Lev Landau)命名的 "朗道极"(Landau pole)只能说明计算方法失败了,而不能说明强力的情况。确定 α s 在远距离上的作用至关重要。
A breakthrough has finally emerged from a wide-ranging effort by many physicists. The tale unfolds in three stages, and one of us played a part in each.
在众多物理学家的广泛努力下,终于取得了突破性进展。这个故事分三个阶段展开,而我们中的每一个人都参与了其中。
The first step was fortuitous. In the late 1990s Deur was a Ph.D. student taking data at the Thomas Jefferson National Accelerator Facility (Jefferson Lab) in Virginia, which houses a particle accelerator. His measurements spanned the transition between short distances and Terra Damnata. At the time, he knew of the Landau pole but not that it was bogus. He was puzzled to see that nothing seemed to happen at the distance where αs should noticeably change (or so he thought). The data were completely smooth, with no sign of the blowup he had been led to expect. The measurements didn’t seem to bother more experienced scientists, who were accustomed to collecting data in this region, and there are only so many naive questions that students can ask before exhausting their welcome. So he added this issue to the long list of things that he didn’t understand about the world, to be answered (maybe) later, and moved on.
第一步是偶然的。20 世纪 90 年代末,迪尔还是一名博士生,在弗吉尼亚州的托马斯-杰斐逊国家加速器设施(杰斐逊实验室)采集数据。他的测量跨越了短距离和泰拉-丹纳塔之间的过渡。当时,他知道朗道极点,但不知道它是假的。他很困惑地发现,在 α s 应该发生明显变化的距离上,似乎什么都没有发生(他是这么认为的)。数据完全平滑,没有他所预期的爆炸迹象。测量结果似乎并没有让经验丰富的科学家感到困扰,因为他们已经习惯了在这一区域收集数据。于是,他把这个问题加入了他对这个世界不了解的一长串问题中,(也许)以后会有答案,然后继续前进。

Jen Christiansen 詹-克里斯蒂安森
A few years later he used his data and other measurements from Jefferson Lab to measure a quantity called the Bjorken integral, named after James Bjorken, one of the pioneers of strong force studies. The Bjorken integral has to do with the direction of quark spin inside protons and neutrons, and as a bonus, it also provides a relatively easy way to calculate αs, as long as you stay away from Terra Damnata. So Deur was able to measure αs on the sure-footed domain of short distances. Being curious and inclined to experiment, he also checked what the formula would predict for long distances. This experiment was just for fun, and he knew very well that he wasn’t supposed to take the answer seriously. But his analysis showed that, far from drastically changing as the distance grew, αs stopped growing and became constant.
几年后,他利用自己的数据和杰斐逊实验室的其他测量结果,测出了一个叫做比约肯积分的量,这个量是以强力研究的先驱之一詹姆斯-比约肯(James Bjorken)的名字命名的。比约肯积分与质子和中子内部的夸克自旋方向有关,而且作为奖励,它还提供了一种相对简单的方法来计算 α s ,只要你远离 Terra Damnata。因此,德乌尔能够在短距离的稳固领域内测量 α s 。由于好奇心和实验倾向,他还检查了公式对长距离的预测。这个实验只是为了好玩,他很清楚自己不应该把答案当真。但他的分析表明,α s 并没有随着距离的增加而发生剧烈变化,而是停止了增长,变成了常数。
Deur shared this alarming finding with his Ph.D. mentor, Jian-Ping Chen, a Jefferson Lab staff scientist, who remarked that this αs looked like predictions he’d seen before. Digging into past studies, Deur found other instances of coupling calculations becoming constant at long distances, much like what he saw in his data. Perhaps his playful αs calculation revealed the strong force’s genuine behavior after all? It was a stroke of luck because, although no one had realized it yet, the Bjorken integral is uniquely suited for calculations of αs at long distances. Whereas most measurements probe interactions among many quarks (because quarks are never found alone), the Bjorken integral manages to filter out most of the multiquark processes and separate out effects on individual quarks. It turns out, this calculation of αs would not have worked with almost any other type of nucleon data.
Deur 与他的博士导师、杰斐逊实验室的科学家陈建平分享了这一惊人发现。陈建平说,这个 α s 看起来就像他以前看到过的预测。在深入研究过去的研究后,Deur发现了其他耦合计算在远距离变得恒定的例子,这与他在数据中看到的情况很相似。也许,他那有趣的 α s 计算最终揭示了强力的真实行为?这是幸运之举,因为尽管还没有人意识到,比约肯积分非常适合计算远距离的 α s 。大多数测量探究的是许多夸克之间的相互作用(因为从来没有单独发现过夸克),而比约肯积分却能过滤掉大多数多夸克过程,并分离出对单个夸克的影响。事实证明,几乎任何其他类型的核子数据都无法计算 α s 。
Because Deur’s αs possibly made sense, he wondered whether he could show it at physics conferences without too much risk of ridicule. He worried, though, because his measurements seemed to contradict the prevailing wisdom that the intensity of the strong force would keep growing. But he decided to risk it. As it happened, Brodsky attended one of these conferences and helped Deur put the work on firmer theoretical footing. This meeting was the beginning of a fruitful collaboration that continues to this day.
由于德乌尔的 α s 可能是有意义的,他想知道自己能否在物理学会议上展示它,而不会冒太大的被嘲笑的风险。不过,他还是担心,因为他的测量结果似乎与强力强度会持续增长的普遍观点相悖。但他还是决定冒这个险。恰巧,布罗茨基参加了其中的一次会议,并帮助德乌尔将这项工作置于更坚实的理论基础之上。这次会面是双方富有成效合作的开端,这种合作一直持续到今天。
While Deur was exploring αs experimentally, Brodsky was working with Guy de Téramond Peralta and Hans Günter Dosch to develop a new method to compute QCD properties at long distances. Their strategy uses a mathematical device known as holography (often used to study black holes and gravity) to infer how the strong force behaves with large values of αs in our four-dimensional spacetime (three space dimensions plus one time dimension) using results from calculations for gravity done in five dimensions. (Whether the extra dimension that underlies this method represents actual physics or is simply a mathematical tool to simplify the problem, much like the use of imaginary numbers in classical physics, no one knows.) This novel approach to the physics of the strong force, so-called light-front holography, can determine αs at long distances and predict the interactions that confine quarks and gluons within nucleons.
当德乌尔在实验中探索 α s 时,布罗茨基正与盖伊-德-泰拉蒙德-佩拉尔塔(Guy de Téramond Peralta)和汉斯-贡特-多施(Hans Günter Dosch)合作,开发一种计算远距离 QCD 特性的新方法。他们的策略是利用一种被称为 "全息法 "的数学装置(通常用于研究黑洞和引力),利用在五维空间中对引力的计算结果来推断强力在我们的四维时空(三个空间维度加一个时间维度)中α s 的大数值下是如何表现的。(这种方法所依据的额外维度是代表实际物理学,还是仅仅是简化问题的数学工具,就像在经典物理学中使用虚数一样,无人知晓)。这种研究强力物理学的新方法,即所谓的光前全息法,可以确定远距离的α s ,并预测将夸克和胶子限制在核子内的相互作用。
Brodsky had long been acquainted with αs and knew that attempts to find a unified theory of the electromagnetic, weak and strong forces seemed to require that αs become finite at long range. In fact, he expected such an outcome because quarks are confined within nucleons, which means quark and gluon quantum loops cannot grow larger than the size of the proton. No more loops means no more evolution of the coupling. So although Deur’s measurements of αs did not surprise him, he was delighted to see that it was, in fact, possible to measure αs at long distances and that the result showed constancy.
布罗茨基很早就了解α s ,他知道,要找到电磁力、弱力和强力的统一理论,似乎需要α s 在远距离上变得有限。事实上,他预料到了这样的结果,因为夸克被限制在核子内,这意味着夸克和胶子量子环的增长不可能超过质子的大小。没有更多的环意味着耦合不再演化。因此,尽管德乌尔对 α s 的测量结果并没有让他感到惊讶,但他很高兴地看到,事实上,在远距离测量 α s 是可能的,而且结果显示出恒定性。
Brodsky and de Téramond Peralta contacted Deur to discuss how to compute αs using their light-front holography method and went on to calculate it. The result, published in 2010, was gratifying: their αs matched Deur’s experimental data exquisitely. It was all the more remarkable because the calculation had no adjustable parameter. They neither fiddled with settings nor messed with “fudge” factors.
Brodsky 和 de Téramond Peralta 联系了 Deur,讨论如何利用他们的光前全息法计算 α s ,并继续计算。2010 年发表的结果令人欣慰:他们的 α s 与德乌尔的实验数据完全吻合。更为难得的是,计算中没有可调参数。他们既没有摆弄设置,也没有使用 "模糊 "系数。
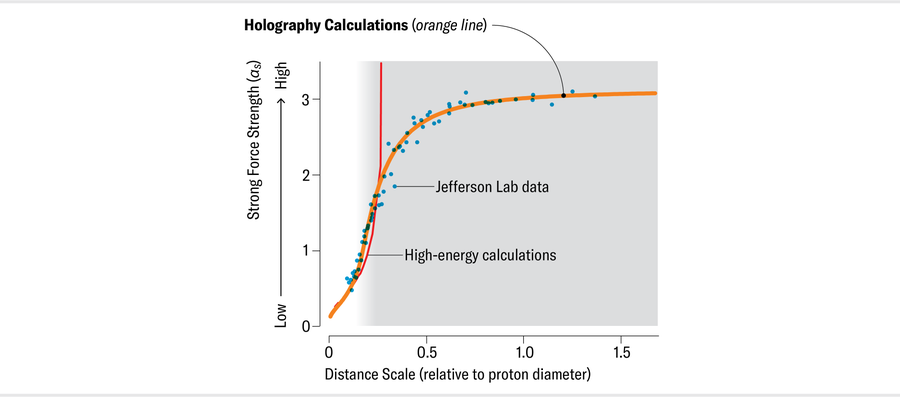
Jen Christiansen 詹-克里斯蒂安森
Of course, holography is an exciting, novel approach to quantum chromodynamics (and quantum gravity), but it’s not the same as using QCD itself. But we know that it at least models QCD very well, suggesting future physicists might be able to prove some kind of equivalence between the behavior of gravity and the strong force. Still, to feel comfortable saying we’d truly calculated αs at long distances, we needed a QCD-based computation. A natural approach is to solve the theory’s equations of motion, which in QCD describe how all strong force quantities evolve as spacetime changes.
当然,全息技术是量子色动力学(和量子引力)的一种令人兴奋的新方法,但它与使用 QCD 本身并不相同。但我们知道,它至少很好地模拟了 QCD,这表明未来的物理学家或许能够证明引力和强力之间的某种等效性。尽管如此,要想安心地说我们真正计算出了远距离的 α s ,我们需要一种基于 QCD 的计算方法。一种自然的方法是求解理论的运动方程,QCD 中的运动方程描述了所有强力量如何随着时空变化而演变。
Deur published his first results on αs in 2005, almost 20 years ago. At the time, Roberts puzzled over them, asking himself what relevance this coupling measurement, seemingly associated exclusively with a single QCD process, could have to the theory’s equations of motion. Such equations need a universal coupling that’s the same for all processes. He put this question aside and moved on.
2005年,也就是将近20年前,罗伯茨发表了他关于α s 的第一个结果。当时,罗伯茨对这些结果百思不得其解,他问自己,这种看似只与单一 QCD 过程相关的耦合测量,对理论的运动方程有什么意义。这些方程需要一个对所有过程都相同的通用耦合。他把这个问题搁置一边,继续前进。
Nine years later, during a 2014 meeting that he and colleagues organized at the European Center for Theoretical Studies in Nuclear Physics and Related Areas in Trento, Italy, he returned to Deur’s αs. Until this point, theorists had employed two parallel strategies to use QCD’s equations of motion to understand the theory of the strong force. The “top-down” approach tried to predict αs through the properties of gluons. The “bottom-up” approach aimed to use directly measurable quantities to infer αs by comparing predictions with experimental data.
九年后,2014 年在意大利特伦托欧洲核物理及相关领域理论研究中心(European Center for Theoretical Studies in Nuclear Physics and Related Areas)举行的一次会议上,他和同事们又回到了 Deur 的 α s 。在此之前,理论家们采用了两种并行的策略,利用 QCD 的运动方程来理解强力理论。自上而下 "的方法试图通过胶子的特性来预测 α s 。而 "自下而上 "的方法则旨在通过比较预测值和实验数据,利用可直接测量的量来推断 α s 。
At that 2014 meeting, a prominent colleague pointed out that the two approaches were delivering vastly different results that couldn’t be reconciled. That colleague, however, was unaware of recent progress with the bottom-up approach that Roberts had made with his collaborator Lei Chang. Within 24 hours, spurred by the challenge, the two had results in hand for the bottom-up coupling estimate. They shared them with two leading players in the top-down area who were also at the meeting, Daniele Binosi and Joannis Papavassiliou, and together the group established that the top-down and bottom-up results for αs were mutually compatible. The parallel streams were merged.
在2014年的那次会议上,一位著名的同事指出,这两种方法得出的结果大相径庭,无法调和。然而,这位同事并不知道罗伯茨与合作者张磊最近在自下而上方法上取得的进展。在挑战的激励下,两人在 24 小时内就得到了自下而上耦合估计的结果。他们与同时参加会议的两位自上而下领域的领军人物达尼埃莱-比诺西(Daniele Binosi)和乔安尼斯-帕帕瓦西利乌(Joannis Papavassiliou)分享了这些成果,并共同确定α s 的自上而下和自下而上的结果是相互兼容的。两个平行小组合并了。
Now we were left with a key question: How do we connect Deur’s coupling measurements and the value we compute using QCD’s equations of motion? If we can do that, then we will have bridged the final gap.
现在我们面临一个关键问题:我们如何将 Deur 的耦合测量值与我们利用 QCD 运动方程计算出的值联系起来?如果我们能做到这一点,那么我们就弥补了最后的差距。
Roberts’s next step was to speak with physicist José Rodríguez-Quintero, who had long been working on the top-down approach and had access to results from computer simulations of QCD. After some back-and-forth brainstorming along with Binosi, Papavassiliou and a new team member, Cédric Mezrag, the group arrived at a universal QCD coupling. Amazingly, this result was virtually indistinguishable from both Deur’s data and the holography calculation by Brodsky and his colleagues. Moreover, like the holography result, the new prediction was parameter-free: no nudging or tinkering. That fact meant that the agreement was deeply significant.
罗伯茨的下一步是与物理学家何塞-罗德里格斯-金特罗(José Rodríguez-Quintero)交谈,后者长期以来一直在研究自上而下的方法,并能获得 QCD 的计算机模拟结果。经过与比诺西、帕帕瓦西利乌和团队新成员塞德里克-梅兹拉格的来回头脑风暴,研究小组得出了一种通用的 QCD 耦合。令人惊讶的是,这一结果与德乌尔的数据和布罗茨基及其同事的全息计算结果几乎没有区别。此外,与全息计算结果一样,新的预测也是无参数的:没有任何推移或修补。这一事实意味着两者的一致具有深远的意义。
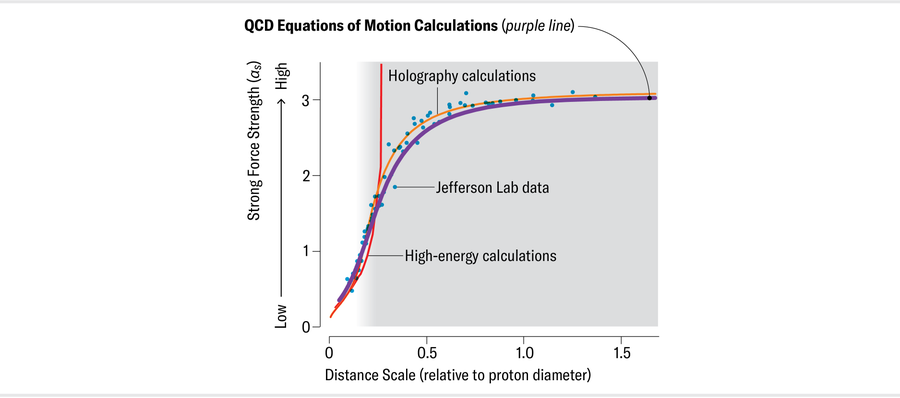
Jen Christiansen 詹-克里斯蒂安森
Since that time, capitalizing on improved information from the top-down, bottom-up and simulation approaches, the group has updated its theoretical analysis. The scientists found that, outside Terra Damnata, their coupling and Deur’s data agree to better than 1 percent. Furthermore, moving into Terra Damnata, they discovered that complex interactions between quarks, which could have upset the connection between these couplings, largely cancel out among themselves because of the physical features of the processes underlying the Bjorken integral. This was Deur’s stroke of luck: he had serendipitously chosen the one process whose coupling is most closely related to the universal result derived from QCD’s equations of motion.
此后,利用自上而下、自下而上和模拟方法获得的改进信息,研究小组更新了理论分析。科学家们发现,在Terra Damnata之外,他们的耦合与Deur的数据吻合度优于1%。此外,在进入 Terra Damnata 后,他们发现夸克之间的复杂相互作用可能会破坏这些耦合之间的联系,但由于比约肯积分所依据的过程的物理特征,这些相互作用在很大程度上相互抵消了。这就是德乌尔的幸运之处:他偶然选择了一个过程,这个过程的耦合与 QCD 运动方程得出的普遍结果关系最为密切。
Now, for the first time, we have both compelling data and calculations of αs that cover the entire length-scale range, including Terra Damnata, the previously unreachable territory. The key finding is that as the distance grows greater, the coupling stops growing, and the inconstant constant becomes constant once more. This discovery has profound implications.
现在,我们首次获得了关于 α s 的令人信服的数据和计算结果,这些数据和计算结果覆盖了整个长度尺度范围,包括之前无法触及的领域 Terra Damnata。关键的发现是,随着距离的增大,耦合停止增长,不稳定常数再次变为常数。这一发现具有深远的意义。

The CEBAF Large Acceptance Spectrometer took some of the measurements that helped to define the strong force at a scale never possible before.
Courtesy of Jefferson Lab
CEBAF 大型接受谱仪进行了一些测量,这些测量有助于以前所未有的规模定义强力。
First, knowing αs at all distances is practically important: physicists can now analytically predict numerous quantities that were previously out of reach. Most phenomena relating to the strong force in nature, from the deepest structure of the atoms within us to the inner workings of neutron stars, are determined by the strength of αs. Because this coupling is dominated by its long-range behavior, which we now know to be finite rather than infinite, we have opened up a new world of possible calculations.
首先,了解所有距离上的α s 具有重要的实际意义:物理学家现在可以通过分析预测许多以前无法预测的量。自然界中与强力有关的大多数现象,从我们体内原子的最深层结构到中子星的内部运作,都是由α s 的强度决定的。由于这种耦合是由其长程行为主导的,而我们现在知道它是有限的而不是无限的,因此我们为可能的计算开辟了一个新世界。
At a deeper level, the solutions of QCD’s equations of motion help to reveal the origin of 99 percent of the visible mass in our universe. This mass comes from atoms, and most of the mass of atoms is in their protons and neutrons (electrons are relatively light). But where does proton and neutron mass come from? The quarks that constitute them also have very little mass of their own. But at the scale of a proton, our revelations about αs suggest that quarks gather clouds of gluons around them that generate much of the mass of the proton. In essence, the powerful binding energy that the strong force exerts to bind quarks together contributes almost all of the mass (remember, Albert Einstein revealed that energy and mass are two sides of the same coin). Therefore, if you weigh 160 pounds, then more than 158 of them come from quantum chromodynamics, specifically because of the mechanism that freezes αs into a constant. The Higgs boson contributes only the small remainder—the tiny mass the quarks and electrons possess on their own.
从更深层次来看,QCD 运动方程的解有助于揭示宇宙中 99% 可见质量的来源。这些质量来自原子,而原子的大部分质量来自质子和中子(电子相对较轻)。但质子和中子的质量从何而来呢?构成它们的夸克本身的质量也很小。但是,在质子的尺度上,我们对 α s 的发现表明,夸克在它们周围聚集的胶子云产生了质子的大部分质量。从本质上讲,强力将夸克结合在一起所产生的强大束缚能几乎贡献了质子的全部质量(请记住,爱因斯坦揭示了能量和质量是一枚硬币的两面)。因此,如果你的体重是 160 磅,那么其中超过 158 磅来自量子色动力学,特别是由于将 α s 冻结为常数的机制。希格斯玻色子只贡献了剩余的一小部分--夸克和电子自身所拥有的微小质量。
Even more significantly, the static nature of αs at long distances means that QCD is the first full quantum field theory that predicts only finite quantities. All the other known quantum field theories, including quantum electrodynamics (which describes the electromagnetic force), run into infinite Landau poles at very high energies. As such, QCD may lead the way to explaining many phenomena that lie outside our current understanding.
更重要的是,α s 在远距离上的静态性质意味着,QCD 是第一个只预测有限量的完整量子场论。所有其他已知的量子场论,包括量子电动力学(描述电磁力),都会在极高能量下遇到无限朗道极。因此,QCD 可能会引领我们去解释许多我们目前无法理解的现象。
Pursuing this line of reasoning, we may learn, for example, whether string theories with 10, 11 or 26 dimensions of spacetime are necessary to make sense of our universe or whether, instead, a clear understanding of our solidly established four spacetime dimensions will turn out to be sufficient. The excitement right now among nuclear and particle physicists is tangible.
根据这一推理思路,我们可能会了解到,例如,时空的 10 维、11 维或 26 维弦理论是否是我们理解宇宙的必要条件,或者,对我们牢固确立的四个时空维度的清晰理解是否就足够了。核物理学家和粒子物理学家现在的兴奋之情溢于言表。