1 Introduction 1 簡介

The last decade has witnessed considerable progress in the development of multiscale entropy method [1], especially for the analysis of physiological time series in revealing underlying complex dynamics of the system. The concept of entropy has been widely used to measure complexity of a system. The idea was initially developed from the classic Shannon entropy [2]. In mathematics, the Shannon entropy of a discrete random variable X is defined as: H(X)=−∑xP(x)log2[P(x)], where P(x) is the probability that X is in the event x, and P(x)log 2[P(x)] is defined as 0 if P(x) = 0. From the equation, if one of the events occurs more frequent than others, observation of that event bears less informative. Conversely, less frequent events provide more information when observed. Entropy is calculated as zero when the outcome is certain. Thus, given a known probability distribution of the source, Shannon entropy quantifies all these considerations exactly, providing a way to estimate the average minimum number of bits needed to encode a string of symbols, based on the frequency of the symbols, which also provides a basis for the ensuing development within the framework of information theory. Among many entropy measures developed such as Kolmogorov–Smirnov (K–S) entropy [3], E–R entropy [4] and compression entropy [58], approximate entropy (ApEn) [5] has been highlighted as one of most effective methods to provide a relatively robust measure of entropy, particularly for short and noisy time series. Sample Entropy [6], as a further development, was used to correct the bias of the ApEn algorithm. All these entropy methods did not consider the multiscale nature of the underlying signals, thus could yield misleading results for complex multiscale system [1]. In reality the signals derived from physiological and complex systems usually have multiple spatiotemporal scales. Therefore, the multiscale entropy [1] was proposed as a new measure of complexity in order to scrutinize complex time series by taking into account different scales. Since its first application to analysis of human heartbeat time series signal [1, 7], the multiscale entropy has been increasingly applied to analyze not only cardiovascular signal [8,9,10], but also many different physiological time series signals for various applications. For instance, the multiscale entropy has been employed to perform the analysis of (1) electroencephalogram [11, 12], functional magnetic resonance imaging [13] and magnetoencephalogram [14] signals to investigate the nonlinear dynamics in brain; (2 the gait time series to explore the gait dynamic [15]; (3) the laser speckle contrast images to examine the aging effect on microcirculation [16]; (4) the lung sound signal to classify the different lung status [17] and (5) the alternative medicine study [18]. In addition to the physiological signal, the multiscale entropy recently has also been utilized to the mechanic fault detection [19,20,21], the characterization of the physical structure of complex system [22,23,24], nonlinear dynamic analysis of financial market [25,26,27,28,29], complexity examination of traffic system [30, 31] and the nonlinear analysis in geophysics [32,33,34].
過去十年見證了多尺度熵方法[1]的發展取得了長足的進步，特別是在生理時間序列分析方面，揭示了系統潛在的複雜動力學。熵的概念已被廣泛用於衡量系統的複雜性。這個想法最初是從經典的香農熵[2]發展而來。在數學中，離散隨機變數 X 的香農熵定義為： H(X)=−∑xP(x)log2[P(x)] ，其中 P(x) 是 X 在事件 x 中的機率，P(如果P(x) = 0，則x)log 2 [P(x)] 定義為0。資訊較少。相反，發生頻率較低的事件在觀察時會提供更多資訊。當結果確定時，熵計算為零。因此，給定已知的源機率分佈，香農熵準確地量化了所有這些考慮因素，提供了一種根據符號的頻率來估計對符號串進行編碼所需的平均最小位數的方法，這也提供了為資訊理論框架內的後續發展奠定了基礎。在許多已開發的熵度量中，例如Kolmogorov-Smirnov (K-S) 熵[3]、E-R 熵[4] 和壓縮熵[58]，近似熵(ApEn) [5] 被認為是最有效的熵度量之一提供相對穩健的熵測量的方法，特別是對於短且有雜訊的時間序列。樣本熵[6]作為進一步的發展，用於修正 ApEn 演算法的偏差。所有這些熵方法都沒有考慮底層訊號的多尺度性質，因此可能會對複雜的多尺度系統產生誤導性的結果[1]。 實際上，來自生理和複雜系統的訊號通常具有多個時空尺度。因此，多尺度熵[1]被提出作為一種新的複雜度量，以便透過考慮不同尺度來審查複雜的時間序列。自從首次應用於分析人體心跳時間序列訊號[1, 7] 以來，多尺度熵已越來越多地應用於分析心血管訊號[8, 9, 10]，也用於分析各種應用的許多不同的生理時間序列訊號。例如，多尺度熵已被用於對（1）腦電圖[11, 12]、功能性磁振造影[13]和腦磁圖[14]訊號進行分析，以研究大腦中的非線性動力學； （2）步態時間序列，探索步態動態[15]；（3）雷射散斑對比影像，檢查老化對微循環的影響[16]；（4）肺音訊號，對不同的肺部狀態進行分類[17] (5)替代醫學研究[18]除了生理訊號之外，多尺度熵最近也被用於機械故障檢測[19,20,21]，複雜系統物理結構的表徵[19,20,21 ]。 。

In terms of methodological development, the multiscale entropy can be implemented in two steps: (1) extraction of different scales of time series, and (2) calculation of entropy over those extracted scales. In the original development of the multiscale entropy [1], the scales of data are determined by the so-called coarse-grained procedure, whereby the raw time series at individual scale is first divided into the nonoverlapping windows, and each window is then replaced by its average [3], upon which the sample entropy is applied. For instance, to generate the consecutive coarse-grained time series at the scale factor Ґ, the original time series was first divided into nonoverlapping windows of length Ґ and the data points within each window were averaged. For scale one (i.e., Ґ = 1), the coarse-grained time series is simply the original time series. The length of each coarse-grained time series is equal to the length of the original time series divided by the scale factor. This ‘coarse-graining’ procedure essentially represents a linear smoothing and decimation to progressively eliminate the fast temporal component from the original signal, which nonetheless might be suboptimal due to the way the scale is extracted [35]. On the other hand, the sample entropy has been criticized for the inaccurate estimation or too sensitive to the choices of the parameters [36]. For example, in sample entropy, the Heaviside function is employed to assess the similarity between the embedded data vectors, which is like a two-state classifier: the contributions of all the data points inside the boundary are treated equally, while the data points outside the boundary are abandoned. As a result, sample entropy may vary dramatically when the tolerance parameter r is slightly changed. As such, different methods have been developed to improve the multiscale entropy estimation. In this chapter, we aim to provide a systematic review for these algorithms and offer some insight for future directions. In what follows, we specifically focus on two aspects of development: (1) extraction of the scales, and (2) estimation of the entropy. From each step of development of the multiscale entropy method, it has also been seen that the multiscale entropy method has been being utilized in the much expanded areas. Specifically, we provide a short overview on the application of multiscale entropy to the analysis of cardiovascular time series. We finally conclude the chapter with discussions.
在方法發展方面，多尺度熵可以分兩步驟實現：（1）提取不同尺度的時間序列，（2）計算這些提取尺度上的熵。在多尺度熵的最初發展中[1]，資料的尺度是由所謂的粗粒度程序確定的，其中各個尺度的原始時間序列首先被劃分為不重疊的窗口，然後替換每個窗口其平均值[ 3]，並在其上應用樣本熵。例如，為了產生比例因子為 А 的連續粗粒度時間序列，首先將原始時間序列分割成長度為 А 的非重疊窗口，並對每個視窗內的資料點進行平均。對於尺度一（即 А = 1），粗粒化時間序列就是原始時間序列。每個粗粒度時間序列的長度等於原始時間序列的長度除以比例因子。這種「粗粒度」過程本質上代表了一種線性平滑和抽取，以逐步消除原始訊號中的快速時間分量，儘管如此，由於提取尺度的方式，這可能不是最理想的[35]。另一方面，樣本熵因估計不準確或對參數的選擇過於敏感而受到批評[36]。例如，在樣本熵中，使用Heaviside函數來評估嵌入資料向量之間的相似性，這就像一個二態分類器：邊界內的所有資料點的貢獻被同等對待，而邊界外的資料點的貢獻被同等對待。因此，當容差參數 r 稍微改變時，樣本熵可能會發生巨大變化。 因此，已經開發了不同的方法來改進多尺度熵估計。在本章中，我們的目標是對這些演算法進行系統性回顧，並為未來的方向提供一些見解。接下來，我們具體關注兩個方面的開發：（1）尺度的提取，（2）熵的估計。從多尺度熵方法的每一步發展也看到，多尺度熵方法的應用領域已經大大擴展。具體來說，我們簡要概述了多尺度熵在心血管時間序列分析中的應用。我們最後透過討論來結束這一章。

2 Overview of Multiscale Entropy
2 多尺度熵概述

The multiscale entropy [1] was developed to measure the complexity/irregularity over the different scales of time series. The scales are determined by the ‘coarse-grained’ procedure, where the length of the coarse-grained time series is equal to the length of original time series divided by the scale factor. At each time scale, sample entropy is used to determine the amount of irregularity to provide the entropy estimation. The sample entropy is thought of as a robust measure of entropy at a single scale due to its insensitivity to the data length and immunity to the noise in the data [6]. It is equal to the negative natural logarithm of the conditional probability that m consecutive points that repeat themselves, within some tolerance, r, will again repeat with the addition of the next (m + 1) point.
多尺度熵 [1] 的發展是為了測量不同尺度時間序列的複雜度/不規則性。尺度由「粗粒度」過程決定，其中粗粒度時間序列的長度等於原始時間序列的長度除以尺度因子。在每個時間尺度，樣本熵用於確定不規則性的量以提供熵估計。樣本熵被認為是單一尺度上熵的穩健度量，因為它對資料長度不敏感並且對資料中的雜訊具有免疫力[6]。它等於在一定容差 r 內重複的 m 個連續點在加入下一個 (m + 1) 個點後再次重複的條件機率的負自然對數。

To compute sample entropy, a time series I = {i(1), i(2),  … , i(N)} is first embedded in a m-dimensional space, in which the m-dimensional vectors of the time series are constructed as x m (k) = (i(k), i(k + 1),  … , i(k + m − 1)) , k = 1 ∼ N − m + 1. In the embedded space, the match of any two vectors is defined as their distance lower than the tolerance r. The distance between two vectors refers to as the maximum difference between their corresponding scalar components. B m(r) is defined as the probability that two vectors match within a tolerance r in the m-dimensional space, where self-matches are excluded. Similarly, A m(r) is defined in the m + 1 dimensional space. Sample entropy is then defined as the negative natural logarithm of the conditional probability that two sequences similar for m points remain similar at the next m + 1 point in the data set within a tolerance r, which is calculated as:
為了計算樣本熵，首先將時間序列 I = {i(1), i(2), … , i(N)} 嵌入到 m 維空間中，其中時間序列的 m 維向量為構造為x m (k) = (i(k), i(k + 1), … , i(k + m − 1)) , k = 1 ∼ N − m + 1。個向量的匹配被定義為它們的距離小於容差r。兩個向量之間的距離是指它們對應的標量分量之間的最​​大差。 B m (r) 定義為 m 維空間中兩個向量在容差 r 內匹配的機率，其中排除自匹配。類似地，A m (r)被定義在m+1維空間。然後，樣本熵定義為在容差 r 內，兩個在 m 個點上相似的序列在資料集中的下一個 m + 1 個點上保持相似的條件機率的負自然對數，計算公式為：

SampEn(I,m,r)=−ln⁡(Am(r)Bm(r))

As a result, regular and/or periodic signals have theoretical sample entropy of 0, whereas uncorrelated random signals have maximum entropy depending on the signal length.

The multiscale entropy can then be obtained by applying the sample entropy across multiple time scales. This is achieved through a coarse-graining procedure, whereby, i.e., at the scale n, the raw time series first is divided into the nonoverlaping windows with the length of n, and each window is then replaced by its average. For instance, at the first scale, the multiscale entropy algorithm evaluates sample entropy for the original time-series. For the second scale (i.e., n = 2), the original time-series (length L) is first divided into non-overlapping windows of length 2. Within each window the average is taken, resulting in a new time-series of length L/2, over which the sample entropy is computed. The procedure is repeated until the last time scale is accomplished. Therefore the coarse-grained procedure essentially represents a linear smoothing and decimation (down sampling) of the original time series. Despite the wide applications, the multiscale entropy approach however has several limitations:

  1. 1.

    The coarse-graining procedure has the effect of down sampling on original time series, which reduces the original sampling rate of a time series to a lower rate, losing the high-frequency component of the signal. Thus, the multiscale entropy only captures the low-frequency components and thus does not entail the high-frequency components as the scales were extracted. Yet there is little reason to ignore the high-frequency components in signal, which may retain significant information in the system [35, 37].

  2. 2.

    Due to the linear operations, the algorithm for extracting the different scales is not well adapted to nonlinear/nonstationary signals, particularly in physiological system. Considering the coarse-grained process as a filter, the features of its frequency response are poor since it shows side lobes in the stopband [35, 38].

  3. 3.

    With ‘Coarse-graining’, the larger the scale factor, the shorter the coarse-grained time series. As the scale increases, the number of data points is reduced [39, 40]. The variance of the estimated entropy gets quickly increased; hence the statistical reliability of entropy measure is greatly diminished.

As a result, several methods have been proposed to overcome these shortcomings. We will review those improvements by focusing on the extraction of the scales and the enhancements of entropy estimation. Table 4.1 below briefly summarizes the key information for these methods.

Table 4.1 Summary of developed multiscale entropy methods
Full size table

3 Methods for Scale Extraction

3.1 Composite Multiscale Entropy

The composite multiscale entropy [39] was developed to address the statistical reliability issue of the multiscale entropy. As described above, in original development of multiscale entropy, the length of coarse-grained time series is shorter when the scale factor becomes larger, leading to the larger variance of sample entropy estimation at greater scales. Thus large variance of estimated entropy values results in the reduction of reliability of multiscale entropy estimation.

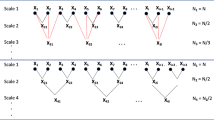
To address this issue, the composite multiscale entropy was developed to first generate multiple unique coarse-grained time series at a certain scale factor (e.g., 3) by changing the starting point (e.g., 1st, 2nd, 3rd) of time series in the coarse-graining procedure, and then calculate sample entropy on each coarse-grained time series, and finally take average of all the calculated sample entropy values. Such a modified coarse-graining procedure is illustrated in Fig. 4.1.

Fig. 4.1
figure 1

The modified coarse-graining procedure used by composite multiscale entropy

Full size image

As shown in [39], both the simulated (e.g., white noise and 1/f noise) and real vibration data (e.g., Figs. 8 and 10 in [39]) show that the composite multiscale entropy yielded the almost same mean estimation with the multiscale entropy, but with much more accurate individual estimation, which is manifested as the smaller standard deviation values of entropy estimation on scales by the composite multiscale entropy than those by the multiscale entropy.

Subsequently, the composite multiscale entropy [40] was refined to further improve the performance in terms of entropy estimation, as it was observed that in composite multiscale entropy, though the multiple coarse-grained time series at individual scales facilitate the accurate estimation of entropy, the method also increases the probability of inducing undefined entropy. Instead of calculating average of sample entropy values over all the coarse-grained time series at single scale, the refined composite multiscale entropy first collected the number of matched patterns over all the coarse-grained time series for the selected parameter m (i.e., collecting the numbers of the matched patterns for both m and m + 1, according to the sample entropy algorithm), and then applied the sample entropy algorithm to calculate the negative natural logarithm of the conditional probability, hence reducing the probability of undefined entropy values. In the Reference [40], the simulated data (white noise and 1/f noise) showed that the refined composite multiscale entropy is superior to both the multiscale entropy and composite multiscale entropy by increasing the accuracy of entropy estimation and reducing the probability of inducing undefined entropy, particularly for short time series data. This can be clearly seen from the Table 2 in [40] that the refined composite multiscale entropy can still work on the shorter time series data and provide the smaller standard deviation of entropy estimations on scales than multiscale entropy and composite multiscale entropy. Furthermore, the refined composite multiscale entropy can be further improved by incorporating with empirical mode decomposition (EMD) algorithm for the purpose of removing the data baseline before calculating the entropy [41].

It should be mentioned that by the same idea of composite multiscale entropy in generating multiple coarse-grained time series, the so-called short-time multiscale entropy [42] was independently developed to address the issue of multiscale entropy when facing with short time series data.

3.2 Modified Multiscale Entropy for Short Time Series

As indicated by its name, the modified multiscale entropy was proposed to address the reliability of multiscale entropy when time series is short [43]. With the same rationale as the above-mentioned composite multiscale entropy, this method tended to offer the better accuracy of entropy estimation or fewer undefined entropy when the time series is short. In essence, the modified multiscale entropy replaced the coarse-graining procedure with a moving-average process, in which a moving window with length of scale factor was slid through the whole time series point-by-point to generate the new time series at the scale. By doing so, data length was largely reserved, compared to the coarse-graining procedure. For instance, at the scale of 2, a time series with 1000 data points is changed into a new time series with 500 data points by the coarse graining procedure, while by the moving-average procedure, the new time series becomes 999 data points.

In [43], both simulation (white noise and 1/f noise) and real vibration data were performed to validate the effectiveness of proposed method for short time series data. For both white noise and 1/f noise with 1 k data points, the modified multiscale entropy provides the sample entropy curve with the less fluctuation than the conventional sample entropy in a typical example. By using 200 independent noise samples for both white noise and 1/f noise, each noise sample contained 500 data points, the results show that the modified multiscale entropy offers the nearly equal mean of entropy estimations with the sample entropy over independent samples, but with the less the standard deviation of entropy estimations than the sample entropy, indicating that the modified multiscale entropy and multiscale entropy methods are nearly equivalent statistically; however, the former method can provide a more accurate estimate than the conventional multiscale entropy. The applications of methods to the real bearing vibration data also show the consistent conclusions. However, it should be mentioned that considering the computational cost and the limited improvement for longer time series, the modified multiscale entropy is not suitable for direct application in analyzing longer time series. For instance, from the Table 2 in [43], it is seen that for the 1/f noise with data length of 30 k, the modified multiscale entropy provides the almost same entropy estimations (including mean and standard deviation over independent samples) with the sample entropy, but demanding significantly heavier computational cost.

3.3 Refined Multiscale Entropy

The refined multiscale entropy [38] is a method to address two drawbacks of the multiscale entropy: (1) the ‘coarse-graining’ procedure can be considered as applying a finite-impulse response (FIR) filter to the original series x and then downsampling the filtered time series with the scale factor, in which frequency response of the FIR filter can be characterized as a very slow roll-off of the main lobe, large transition band, and important side lobes in the stopband, thus introducing aliasing when the subsequent downsampling procedure is applied; and (2) the parameter r for determining the similarity between two patterns remains constant for all the scales as a percentage of standard deviation of the original time series, thus leading to artificially decreasing entropy rate, as the patterns more likely becomes indistinguishable at higher scale in such a setting.

In order to overcome both shortcomings, the refined multiscale entropy (1) replaced the FIR filter with a low-pass Butterworth filter, whose frequency response was flat in the passband, side lobes in the stopband were not present, and the roll-off was fast, thus ensuring a more accurate elimination of the components and reducing aliasing when the filtered series were downsampled; and (2) let parameter r be continuously updated as a percentage of the standard deviation (SD) of the filtered series, thus compensating the decrease of variance with the elimination of the fast temporal scales.

The performance of the refined multiscale entropy was verified and examined by Gaussian white noise, 1/f noise and autoregressive processes, as well as real 24-h Holter recordings of heart rate variability (HRV) obtained from healthy and aortic stenosis (AS) groups. It is worth noting that the results of Gaussian white noise and 1/f noise by the refined multiscale entropy are opposite to those obtained via the multiscale entropy. The main reason leading to this discrepancy is that two methods apply the different calculations of the similarity parameter, r for the coarse-graining procedure. In the original multiscale entropy, the parameter r remains constant for all scale factors as a percentage of standard deviation of the original time series [1], whereas the parameter r in the refined multiscale entropy is continuously updated as a percentage of the standard deviation of the filtered series [38]. It has been pointed out [38] that the coarse-graining procedure in original multiscale entropy eliminates the fast temporal scales as the scale factor increases, acting as a low-pass filter. As such, the coarse-grained series are usually characterized by a lower standard deviation compared to the original time series. Thus, if the parameter r is kept constant for all the scales, more and more patterns will be considered similar with the increasing scale factor, hence increasing estimated regularity and reporting artificially decreasing entropy with the scale factor.

3.4 Generalized Multiscale Entropy

The generalized multiscale entropy [44] was developed to generalize the multiscale entropy. In the coarse-graining procedure, a time series was first divided into non-overlapping segments with the length of scale factor, and then the average was taken within each segment, which can been thought as the first moment. Instead of the first moment, the generalized multiscale entropy was proposed to use an arbitrary moment (e.g., volatility when the second moment) to generate the coarse-grained time series for entropy analysis. This approach may offer a new way to explain the calculated entropy results. For instance, when using the second moment, the multiscale entropy represents the multiscale complexity of the volatility of data. This approach has been applied to study cardiac interval time series from three groups, comprising health young and older subjects, and patients with chronic heart failure syndrome [44]. The results show that the complexity indices of healthy young subjects were significantly higher than those of healthy older subjects, whereas the complexity indices of the healthy older subjects were significantly higher than those of the heart failure patients. These results support their hypothesis that the heartbeat volatility time series from healthy young subjects are more complex than those of healthy older subjects, which are more complex than those from patients with heart failure.

3.5 Intrinsic Mode Entropy

The intrinsic mode entropy [37] identified two shortcomings of the multiscale entropy: (1) the high-frequency components were eliminated by the coarse-graining procedure, which may contain relevant information for some physiological data, and (2) the coarse-graining procedure, while extracting the scales, may be not adapted to nonstationary/nonlinear signal, which is quite common in the physiological systems.

The intrinsic mode entropy was proposed to directly address these issues by exploiting a fully adaptive, data-driven time series decomposition method, namely empirical mode decomposition (EMD) [45], to extract the scales intrinsic to the data. The EMD adaptively decomposes a time series signal, by means of the so-called the sifting method, into a finite set of amplitude- and/or frequency-modulated (AM/FM) modulated components, referred to as intrinsic mode functions (IMFs) [45]. IMFs satisfy the requirements that the mean of the upper and lower envelops is locally zero and the number of extrema and the number of zero-crossing differ by at most one, and thus represent the intrinsic oscillation modes of data on the different frequency scales. By virtue of the EMD, the time series x(t) can be decomposed as x(t)=∑j=1kCj(t)+r(t), where C j (t) , j = 1 ,  …  , k are the IMFs and r(t) is the monotonic residue. The EMD algorithm is briefly described as follows.

  1. 1.

    Let x~(t)=x(t);

  2. 2.

    Find all local maxima and minima of x~(t);

  3. 3.

    Interpolate through all the minima (maxima) to obtain the lower (upper) signal envelop e min(t) (e max(t));

  4. 4.

    Compute the local mean m(t)=emin(t)+emax(t)2;

  5. 5.

    Obtain the detail part of signal c(t)=x~(t)−m(t);

  6. 6.

    Let x~(t)=c(t) and repeat the process from step 2 until c(t) becomes an IMF.

Compute the residue r(t) = x(t) − c(t) and go back to step 2 with x~(t)=r(t), until the monotonic residue signal is left.

As such, in the intrinsic mode entropy, a time series is first adaptively decomposed into several IMFs with distinct frequency bands by EMD, and then the multiple scales of the original signal can be obtained by the cumulative sums of the IMFs, starting from the finest scales and ending with the whole signal, over which the sample entropy is applied. The usefulness of intrinsic mode entropy was demonstrated by its application to real stabilogram signals for discrimination between elderly and control subjects.

It bears noting that relying on the EMD method, the intrinsic mode entropy inevitably suffers from both the mode-misalignment and mode-mixing problems, particularly in the analysis of multivariate time series data [46]. The mode-misalignment refers to a problem where the common frequency modes across a multivariate data appear in the different-index IMFs, thus resulting that the IMFs are not matched either in the number or in scale, whereas the mode-mixing is manifested by a single IMF containing multiple oscillatory modes and/or a single mode residing in multiple IMFs which may in some cases compromise the physical meaning of IMFs and practical applications [47]. Both problems can be simply illustrated by a toy example shown in Fig. 4.2. Because the intrinsic mode entropy is applied to each time series separately, these two problems may contribute to inappropriate operation (e.g., comparison) of entropy values at the ‘same’ scale factor from different time series, for the ‘same’ scale from different time series could be in the largely different frequency ranges.

Fig. 4.2
figure 2

Example of mode-mixing and mode-misalignment by original empirical mode decomposition

Full size image

Therefore, an improved intrinsic mode entropy method [46] was introduced to address the potential mode-misalignment and mode-mixing problems based on the multivariate empirical mode decomposition (MEMD), which directly works with multivariate data to greatly mitigate above two problems, generating the aligned IMFs. In this method, the MEMD [48] plays an important role for the extraction of the scales. The MEMD is the multivariate extension of EMD, thus mitigating both mode-misalignment and mode-mixing problems. An important step in the MEMD method, distinct from the EMD, is the calculation of local mean, as the concept of local extrema is not well defined for multivariate signals. To deal with this problem, MEMD projects the multivariate signal along different directions to generate the multiple multidimensional envelops; these envelops are then averaged to obtain the local mean. The details of MEMD can be found in [48]. Figure 4.3 demonstrates the decomposition of same data as in Fig. 4.2 by the MEMD to show that MEMD is effective to produce the aligned IMFs. The application of the improved intrinsic mode entropy approach to real local field potential data from visual cortex of monkeys illustrates that this approach is able to capture more discriminant information than the other methods [49].

Fig. 4.3
figure 3

Decomposition of same data in Fig. 4.2 by multivariate empirical mode decomposition (MEMD), showing the aligned decomposed components

Full size image

Thus far, the EMD family has been extensively used in multiscale entropy analysis [41, 50]. It should be noted that one important extension of EMD, ensemble EMD [47], has also been applied to multiscale entropy method to solve the mode-mixing problem [51, 52]. However, the aligned IMF numbers from different time series are not guaranteed by this method. In addition, to preserve the high frequency component in entropy analysis, the hierarchical entropy was used essentially based on wavelet decomposition [53], which is effective for the analysis of nonstationary time series data.

3.6 Adaptive Multiscale Entropy

The adaptive multiscale entropy (AME) [35] was developed to provide a comprehensive means for the scales extracted from time series including both the ‘coarse-to-fine’ and ‘fine-to-coarse’ scales. The method was specifically to address the issue of multiscale entropy that the high frequency component is eliminated. With the AME, the scale extraction is adaptive, completely driven by the data via EMD, thus suitable for nonstationary/nonlinear time series data. Moreover, by employing the multivariate extension of empirical mode decomposition (i.e., MEMD), the proposed AME can fully address the mode-misalignment and mode-mixing problems induced by univariate empirical mode decomposition for the analysis of individual time series, thus producing the aligned IMF components and ensuring proper operations (e.g., comparison) of entropy estimation at one scale over multiple time series data.

To implement the AME, the MEMD method is first applied to decompose data into the aligned IMFs. The scales are then selected by consecutively removing either the high-frequency or low-frequency IMFs from the original data. The way to select the scales results in two algorithms, namely the fine-to-coarse AME and the coarse-to-fine AME, which essentially represent the multiscale low-pass and high-pass filtering of the original signal, respectively. The sample entropy is applied to the selective scales to estimate the entropy measure. When applying this approach to physiological time series signal (e.g., neural data), two issues [49] had to be solved: (1) the physiological data are often collected over certain time period from multiple channels across many trials, which can be represented as a three-dimensional matrix, i.e. TimePoints × Channels × Trials, thus not directly solvable by the MEMD; and (2) the physiological recordings are usually collected over many trials spanning from days to months, or even years, so that the dynamic ranges of multiple signals are likely to be of high degree of variability, which can have detrimental effect upon the final decomposition of MEMD. Therefore, the AME adopts two important preprocessing steps to accommodating the multivariate data. First, the high-dimensional physiological data (e.g. TimePoints × Channels × Trials) is first reshaped into such a two-dimensional time series as TimePoints × [Channels × Trials] before subject to the MEMD analysis. It is an important step to make sure that all the IMFs be aligned not only across channels, but also across trials. Second, in order to reduce the variability among neural recordings, individual time series in the reshaped matrix is normalized against their temporal standard deviation before the MEMD is applied. After the MEMD decomposition, those extracted standard deviations are then restored to the corresponding IMFs.

Simulations demonstrate that the AME is able to adaptively extract the scales inherent in the nonstationary signal and that the AME works with both the coarse scales and fine scales in the data [35]. The application to real local field potential data in the visual cortex of monkeys suggests that the AME is suitable for entropy analysis of nonlinear/nonstationary physiological data, and outperforms the multiscale entropy in revealing the underlying entropy information retained in the intrinsic scales. The AME method has been further extended as adaptive multiscale cross-entropy (AMCE) [49] to assess the nonlinear dependency between time series signals. Both the AME and AMCE are employed to neural data from the visual cortex of monkeys to explore how the perceptual suppression is reflect by neural activity within individual brain areas and functional connectivity between areas.

4 Methods for Entropy Estimation

4.1 Multiscale Permutation Entropy

The permutation entropy [54], instead of the sample entropy, has been applied to conduct the multiscale entropy analysis [55]. By using the rank order value of embedded vector, the permutation entropy is robust for the time series with nonlinear distortion, and is also computationally efficient. Specifically, with the m-dimensional delay, the original time series is transformed into a set of embedded vectors. Each vector is then represented by its rank order. For instance, a vector, [12, 56, 0.0003, 100,000, 50] can be represented by its rank order, [1,2,3,4,5]. We can see that the rank order is insensitive to the magnitude of the data, though the values may be at largely different scales. Subsequently, for a given embedded dimension (e.g., m dimension), the rate of each possible rank order, out of m! possible rank orders, is calculated over all the embedded vectors, forming a probability distribution over all the rank orders. The Shannon entropy is finally applied to the probability distribution to obtain the entropy estimation.

In the similar fashion, the multiscale symbolic entropy [56] was developed to reliably assess the complexity in noisy data while being highly resilient to outliers. In the time series data, the outliers are often illustrated as those data points with the significantly higher or lower magnitudes than most of data points due to some internal/external uncontrolled influence. In this approach, the variation at a time point consists of both the magnitude (absolute value) and the direction (sign). It is hypothesized that dynamics in the sign time series can adequately reflect the complexity in raw data and that the complexity estimation based on the sign time series is more resilient to outliers as compared to raw data. To implement this method, the original time series at a given scale is first divided into non-overlapped segments, within each of which the median is calculated to generate a coarse-grained time series. The sign time series of the coarse grained signal is then generated by considering the direction of change at each point (i.e., 1 for increasing and 0 otherwise). The discrete probability count and the Shannon entropy are applied to the sign data to obtain the entropy estimation. The multiscale measure is obtained when the above procedure goes over all the predefined scales. This method has been successfully applied to the analysis of human heartbeat recordings, showing the robustness to noisy data with outliers.

4.2 Multiscale Compression Entropy

The multiscale compression entropy [57] has been reported, which replaced the sample entropy with the compression entropy [58] to conduct the multiscale entropy analysis. The basic idea of compression entropy is the smallest algorithm that produces a string is the entropy of that string from algorithmic information theory, which can be approximated by the data compression techniques. For instance, the compression entropy per symbol can be represented by the ratio of compressed text to the original text length, if the length of the text to be compressed is sufficiently large and if the source is an ergodic process. The compression entropy provides an indication to which degree the time series under study can be compressed using the detection of recurring sequences. The more frequent the occurrences of sequences (and thus, the more regular the time series), the higher the compression rate. The ratio of the lengths of the compressed to the uncompressed time series is used as a complexity measure and identified as compression entropy. The multiscale compression entropy exploits the coarse-graining procedure to generate the scales of data, over which the compression entropy is applied. This approach has been applied to the entropy analysis for the microvascular blood flow signals [57]. In this application, microvascular blood flow was continuously monitored with laser speckle contrast imaging (LSCI) and with laser Doppler flowmetry (LDF) simultaneously from healthy subjects. The results show that, for both LSCI and LDF time series, the compression entropy values are less than 1 for all of the scales analyzed, suggesting that there are repetitive structures within the data fluctuations at all scales.

4.3 Fuzzy Entropy

In the family of approximate entropy [5], for example, sample entropy [6], the similarity of vectors (or patterns) from a time series is a key component for accurate estimation of entropy. The sample entropy (and approximate entropy) assesses the similarity between vectors based on the Heaviside function, as shown in Fig. 4.4. It is evident that the boundary of Heaviside function is rigid, which leads to that all the data points inside boundary are treated equally, whereas the data points outside the boundary are excluded no matter how close this point locates to boundary. Thus, the estimation of sample entropy is highly sensitive to the change of the tolerance, r or data point location.

Fig. 4.4
figure 4

Heaviside function (dash dotted black) and fuzzy function (solid blue) for similarity in entropy estimation (modified based on [21]. As figure shown, by the Heaviside function, both points d2 (red) and d3 (red) are considered within the boundary and both similar to the original point (i.e., ‘0’); whereas another point d1 (green), very close to d2 though, is considered dissimilar because it falls just outside the boundary. Thus a slight increase in r will make the boundary encloses the point d1, and then the conclusion totally changes. However, the fuzzy function will largely relieve this issue

Full size image

The fuzzy entropy [36] aimed to improve the entropy estimation at just this point, based on the concept of fuzzy sets [59], which adopted the “membership degree” with a fuzzy function that associates each point with a real number in a certain range (e.g., [0, 1]). The fuzzy entropy employed the family of exponential function as the fuzzy function to obtain the fuzzy measurement of similarity, which bears two desired properties: (1) being continuous so that the similarity does not change abruptly; (2) being convex so that the self-similarity is the maximum. In addition, the fuzzy entropy removes the baseline of the vector sequences, so that the similarity measure more relies on vectors’ shapes rather than their absolute coordinates, which makes the similarity definition fuzzier.

Extensive simulations and application [60] to experimental electromyography (EMG) suggest that the fuzzy entropy is a more accurate entropy measure than the approximate entropy and sample entropy, and exhibits the stronger relative consistency and less dependence on the data length, thus providing an improved evaluation of signal complexity, especially for short time series contaminated by noise. For instance, as shown from the Fig. 4.2 in [60], with only 50 data samples, the fuzzy entropy can successfully discriminate three periodical sinusoidal time series with different frequencies, outperforming the approximate entropy and sample entropy. And from the Fig. 5 in [60], it is observed that the fuzzy entropy can consistently separate the different logistic datasets contaminated by noises with different noise levels, while it becomes difficult for the approximate entropy and sample entropy to distinguish those data. In addition to the exponential function, the nonlinear sigmoid and Gaussian functions have also been used to replace the Heaviside function for similarity measure [61]. The fuzzy entropy was also extended to cross-fuzzy entropy to test nonlinear pattern synchrony of bivariate time series [62]. It has been shown that the fuzzy entropy can be also used in the multiscale entropy analysis by replacing the sample entropy [63, 64].

4.4 Multivariate Multiscale Entropy

The multivariate multiscale entropy [65] was introduced to perform entropy analysis for multivariate time series, which has been increasingly common for physiological data due to the advance in recording techniques. The multivariate multiscale entropy adopts the coarse-graining procedure to extract the scales of data, and then extends the sample entropy algorithm to multivariate sample entropy for entropy estimation of coarse-grained multivariate data. The detailed multivariate sample entropy algorithm can be found in [65]. The simulations and a large array of real-world applications [66] including the human stride interval fluctuations data, cardiac interbeat interval and respiratory interbreath interval data, 3D ultrasonic anemometer data taken in the north-south, east-west, and vertical directions etc., have demonstrated the effectiveness of this approach in assessing the underlying dynamics of multivariate time series.

It is worth to mention that copula can be used to implement multivariate multiscale entropy by incorporating the multivariate empirical mode decomposition and the Renyi entropy [67]. The Renyi entropy (or information) is a probability-based unified entropy measure, which is considered to generalize the Hartley entropy, the Shannon entropy, the collision entropy and the min-entropy. The Renyi entropy has been shown as a robust (multivariate) entropy estimation when its implementation algorithm is based on the copula of multivariate distribution [67]. The copula [68, 69] can be considered as the transformation which standardizes the marginal of multivariate data to be uniform on [0, 1] while preserving many of the distribution’s dependence properties including its concordance measures and its information, which has been widely recognized in many fields, e.g., finance [70, 71], physiology [72,73,74], etc. Thus, the Renyi entropy estimation is based entirely on the ranks of multivariate data, therefore robust to outliers. As such, the application of Renyi entropy to the adaptively extracted scales of multivariate data by the multivariate empirical mode decomposition may provide a potential option to implement multivariate multiscale entropy.

The above multivariate entropy methods all assess the simultaneous dependency for multivariate data, while the transfer entropy [75] has been developed to measure the directed information transfer between time series, revealing a causal relationship between signal rather than correlation. The multiscale transfer entropy [76] makes use of the wavelet-based method to extract multiple scales of data, and then measure directional transfer of information between coupled systems at the multiple scales. This approach has demonstrated its effectiveness by extensive simulations and application to real physiological (heart beat and breathe) and robotic (composed of one sensor and one actuator) data.

5 Multiscale Entropy Analysis of Cardiovascular Time Series

Nonlinear analysis of cardiovascular data has been widely recognized to provide relevant information on psychophysiological and pathological states. Among others, entropy measure has been serving as a powerful tool to quantify the cardiovascular dynamics of a time series over multiple time scales [1] through approximate entropy [5], sample entropy [6] and multiscale entropy [1]. When the multiscale entropy was initially developed, it has been applied to analysis of heart beat signal for diagnostics, risk stratification, detection of toxicity of cardiac drugs and study of intermittency in energy and information flows of cardiac system [1, 44, 77]. In the original publication for the sample entropy [1], the multiscale entropy was applied to analyze the heartbeat intervals time series from (1) healthy subjects, (2) subjects with congestive heart failure, and (3) subjects with the atrial fibrillation. The analysis results of multiscale entropy show that at scale of 20 (note not the original scale) the entropy value for the coarse-grained time series derived from healthy subjects is significantly higher than those for atrial fibrillation and congestive heart failure, facilitating to address the longstanding paradox for the applications of traditional single-scale entropy methods to physiological time series, that is, the traditional entropy methods may yield the higher complexity for certain pathologic processes associated with random outputs than that for healthy dynamics exhibiting long-range correlations, but it is believed that disease states or aging may be defined by a sustained breakdown of long-range correlations and thus loss of information, i.e., less complexity. This work suggests that the paradox may be due to the fact that conventional algorithms fail to account for the multiple time scales inherent in physiologic dynamics, which can be discovered by the multiscale entropy. In addition, the multiscale entropy has been applied, but not limited, to analysis of heart rate variability for the objective quantification of psychological traits through autonomic nervous system biomarkers [78], detection of cardiac autonomic neuropathy [79] and assessing the severity of sleep disordered breathing [80], to analysis of microvascular blood flow signal for better understanding of the peripheral cardiovascular system [57], to analysis of interval variability from Q-waveonset to T-wave end (QT) derived from 24-hour Holter recordings for improving identification of condition of the long QT syndrome type 1 [81] and to analysis of pulse wave velocity signal for differentiating among healthy, aged, and diabetic populations [42]. A typical example of application of multiscale entropy to the heart rate variability analysis [80] is to investigate the relationship between the obstructive sleep apnea (OSA) and the complexity of heart rate variability to identify the predictive value of the heart rate variability analysis in assessing the severity of OSA. In the study, the R-R intervals from 10 segments of 10-min electrocardiogram recordings during non-rapid eye movement sleep at stage N2 were collected from four groups of subjects: (1) the normal snoring subjects without OSA, (2) mild OSA, (3) moderate OSA and (4) severe OSA. The multiscale entropy was applied to perform the heart rate variability analysis, in which the multiple scales were divided into the small scale (scale 1–5) and the large scale (scale 6–10). The analysis results show that the entropy at the small scale could successfully distinguish the normal snoring group and the mild OSA group from the moderate and severe groups, and a good correlation between the entropy at the small scale and the apnea hypopnea index was displayed, suggesting that the multiscale entropy analysis at the small scale may serve as a simple preliminary screening tool for assessing the severity of OSA. Except the heart rate variability signal, the multiscale entropy has been proved as a powerful analysis tool for many other physiological signals, e.g., for analysis of pulse wave velocity signal [42]. In the study, the pulse wave velocity series were recorded from 4 groups of subjects: (1) the healthy young group, (2) the middle-aged group without known cardiovascular disease, (3) the middle-aged group with well-controlled diabetes mellitus type 2 and (4) the middle-aged group with poorly-controlled diabetes mellitus type 2. By applying the multiscale entropy analysis, the results show that the multiscale entropy can produce significant differences in entropies between the different groups of subjects, demonstrating a promising biomarker for differentiating among healthy, aged, and diabetic populations. It is worth to mention that an interesting frontier in nonlinear analysis on heart rate variability (HRV) data was represented by the assessment of psychiatric disorders. Specifically, multiscale entropy was performed on the R-R interval series to assess the heartbeat complexity as an objective clinical biomarker for mental disorders [82]. In the study, the R-R interval data were acquired from the bipolar patients who exhibited mood states among depression, hypomania, and euthymia. Multiscale entropy analysis was applied to the heart rate variability to discriminate the three pathological mood states. The results show that the euthymic state is associated to the significantly higher complexity at all scales than the depressive and hypomanic states, suggesting a potential utilization of the heart rate variability complexity indices for a viable support to the clinical decision. Recently, an instantaneous entropy measure based on the inhomogeneous point-process theory is an important methodological advance [83]. This novel measure has been successfully used for analyzing heartbeat dynamics of healthy subjects and patients with cardiac heart failure together with gait recordings from short walks of young and elderly subjects. It therefore offers a promising mathematical tool for the dynamic analysis of a wide range of applications and to potentially study any physical and natural stochastic discrete processes [84]. With the further advance of multiscale entropy method, it is expected that this method will make much more contributions in discovering the nonlinear structure properties in cardiac systems.

6 Conclusion

This systematic review summarizes the multiscale entropy and its many variations mainly from two perspectives: (1) the extraction of multiple scales, and (2) the entropy estimation methods. These methods are designed to improve the accuracy and precision of the multiscale entropy method, especially when the time series is short and noisy. Given a large cohort of multiscale entropy methods rapidly developed within the past decade, it becomes clear that the multiscale entropy is an emerging technique that can be used to evaluate the relationship between complexity and health in a number of physiological systems. This can be seen, for instance, in the analysis of cardiovascular time series with the multiscale entropy measure. It is our hope that this review may serve as a reference to the development and application of multiscale entropy methods, to better understand the pros and cons of this methodology, and to inspire new ideas for further development for years to come.