Output feedback stabilization of linear systems with infinite (1)Output feedback stabilization of linear systems with infinite (1).pdf

4. 数值示例重试错误原因

{\begin{cases} \dot{x} (t) = A x (t) + \overset{―}{B_{1} u (t - 1}) + \int_{0}^{+ \infty} B_{0} (θ) u (t - θ) d θ \\ y (t) = ϵ_{1} x (t - 0.5) + \overset{―}{\int_{θ}^{+ \infty} C_{0} (θ) x (t - θ) d θ}, \subset) (\leftrightarrow t) \end{cases}

\begin{aligned} A = [\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 3 ω^{2} & 0 & 0 & 0 & 2 ω & 0 \\ 0 & 0 & 0 & - 2 ω & 0 & 0 \\ 0 & 0 & - ω^{2} & 0 & 0 & 0 \end{array}], \\ B_{1} = [\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}], B_{0} (θ) = [\begin{array}{llll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}] ϵ (θ), \\ C_{1} = [\begin{array}{lllll} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 \end{array}], C_{0} (θ) = [\begin{array}{llllll} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \end{array}] ε (θ), \end{aligned}

ω > 0, ϵ (θ)

和

ε (θ)

是上的两个非负函数

[0, \infty)

.可以验证

λ (A) = {0, 0, - ω l, - ω l, ω l, ω l}

，这意味着满足假设 1。让 orbit rate

ω = 7.2722 \times 10^{- 5} rad / s, ϵ (θ) = 4 θ e^{- 2 θ}

和系统状态的初始函数

x (- θ) = [10000, 5000, - 10000, 2, 1, - 3]^{T}, θ \in [0, + \infty)

在实践中，追逐者航天器并不总是能获得目标航天器的完整实时轨道信息。例如，由于目标航天器或地面设备的故障，两个航天器之间没有通信时，就会发生这种情况。因此，采用 Observer （8）来估计系统状态。假设

ρ = 0.01, γ = 0.01, ε (θ) = θ e^{- θ}

和观察者的初始函数

\hat{x} (- θ) = [9500, 5500, - 9600, - 2, 3, - 5]^{T}, θ \in [0, + \infty)

\begin{aligned} B & = e^{- A} B_{1} + \int_{0}^{+ \infty} e^{- A θ} B_{0} (θ) d θ \\ = [\begin{array}{ccc} - 1 & 1.09 \times 10^{- 4} & 0 \\ - 7.27 \times 10^{- 5} & - 1 & 0 \\ 0 & 0 & - 1 \\ 1 & - 1.45 \times 10^{- 4} & 0 \\ 1.45 \times 10^{- 4} & 1 & 0 \\ 0 & 0 & 1 \end{array}], \\ C & = C_{1} e^{- 0.5 A} + \int_{0}^{+ \infty} C_{0} (θ) e^{- A θ} d θ \\ = [\begin{array}{ccccc} 1 & 0 & 0 & - 0.5 & 1.82 \times 10^{- 5} \\ 9.23 \times 10^{- 12} & 1 & 0 & - 4.36 \times 10^{- 4} & - 2 \\ 0 & 0 & 1 & 0 & 0 \end{array}] \end{aligned}

和

L = [\begin{array}{ccc} 0.02 & 0 & 0 \\ 0 & 0.0202 & 0 \\ 0 & 0 & 0.0202 \\ 0.0001 & 0 & 0 \\ 0 & 0.0001 & 0 \\ 0 & 0 & 0.0001 \end{array}]

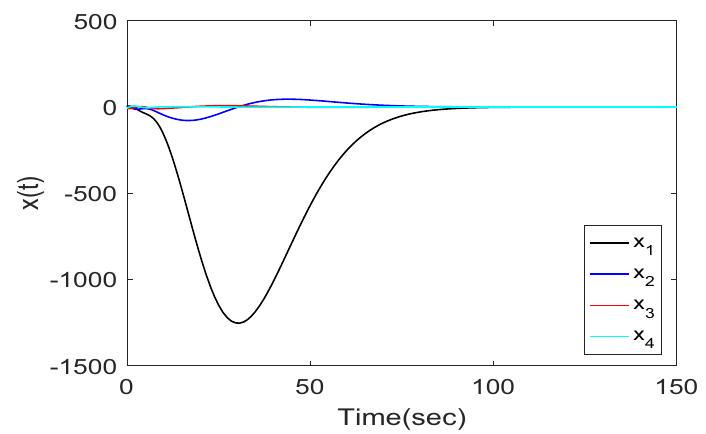
然后我们可以验证假设 2 和 3 是否得到满足。此外，还存在一个非递增函数

h (θ) = 4 e^{- \frac{3}{4} θ} > 0, θ \in [0, + \infty)

使得

\int_{0}^{+ \infty} h (θ) x (- θ) d θ < + \infty

和

\int_{0}^{+ \infty} h (θ) \hat{x} (- θ) d θ < + \infty

.因此，从定理 1 可以得出，控制器（21）下的闭环系统（32）是全局渐近稳定的。状态响应和观察者错误响应分别如图 2 和图 3 所示。可以观察到，state 和 observer 误差最终都接近于 0。重试错误原因

例 4.2.考虑描述惯性轮摆的四阶时滞系统

[27, 40]

{\begin{cases} \dot{x} (t) = A x (t) + B_{1} u (t - 1) + \int_{0}^{+ \infty} B_{0} (θ) u (t - θ) d θ \\ y (t) = C_{1} u (t - 0.5) + \int_{0}^{+ \infty} C_{0} (θ) x (t - θ) d θ \end{cases}

\begin{aligned} A = [\begin{array}{llll} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array}], \\ B_{1} = [\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix}], B_{0} (θ) = [\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix}] 4 θ e^{- 2 θ}, \end{aligned}

C_{1} = [1, 0, 0, 0]

和

C_{0} (θ) = C_{1} ε (θ)

.可以计算出

λ (A)

为零，而

\int_{0}^{+ \infty} 4 θ e^{- 2 θ} d θ = 1

.在这种情况下，因此采用了控制器（30）。选择其他参数和初始条件与 [27] 中的相同。观察者

ver (8)

用于估计系统状态。让

ρ = 0.2, γ = 0.2

和

ε (θ) = θ e^{- θ}

\begin{aligned} B = B_{1} + \int_{0}^{+ \infty} B_{0} (θ) d θ = [0, 0, 0, 2]^{T}, \\ C = C_{1} + \int_{0}^{+ \infty} C_{0} (θ) d θ = \underset{―}{[2, 0, 0, 0]} \end{aligned}

和

L = [0.4, 0.12, 0.016, 0.0008]^{T}

可以验证假设 5 得到满足。因此，我们可以从定理 2 中得出，控制器（30）的闭环系统（33）是全局渐近稳定的。状态响应和观察者错误响应分别在图 4 和 5 中给出。可以观察到，状态误差和观察者误差逐渐收敛为零。重试错误原因

\begin{array}{l} {\begin{matrix} \dot{x} (t) = A x (t) + \int_{0}^{+ \infty} B_{0} (θ) u (t - θ) d θ \\ y (t) = \int_{0}^{+ \infty} C_{0} (θ) x (t - θ) d θ \end{matrix} \\ A = [\begin{array}{cccc} 0 & 1 & 1 & 0 \\ - 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 0 \end{array}], B_{0} = [\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix}] ϵ (θ), C_{0} (θ) = [\begin{array}{lll} 1 & 0 & 0 \end{array}] \end{array}] ε (θ),

ϵ (θ) = e^{- θ}

和

ε (θ) = e^{- 2 θ}, θ \in [0, + \infty)

.一个有

C = \int_{0}^{+ \infty} C_{0} (θ) e^{- A θ} d θ = [0.4, - 0.2, - 0.12, 0.16]

.其他参数和矩阵，即

ρ, B, P

和系统状态的初始函数被选择为 [25] 中的相同。可以验证假设 1-3 得到满足。当系统状态的完整信息可用于反馈控制时，可以从 [25] 获得 [25] 中给出的状态反馈控制器下的系统（34）是全局渐近稳定的。如果系统状态不可用于反馈控制，则采用观察器（8）来估计系统状态。让

γ = 0.1

以及 observer 的初始功能

\hat{x} (- θ) = {[6 e^{\frac{1}{2} θ}, 2 e^{\frac{1}{2} θ}, - 6 e^{\frac{1}{θ} θ}, - 4 e^{\frac{1}{4} θ}]}^{T}, θ \in [0, + \infty)

.可以计算出

L = [0.86, - 0.3179, 0.0419, - 0.016]^{T}

.因此，从定理 1 可以得出，由（34）和控制器（21）组成的闭环系统是全局渐近稳定的。状态响应和观察者错误响应分别如图 6 和图 7 所示。可以观察到，系统状态和观测器误差渐近收敛为零。重试错误原因