Chirp 鸣叫
This article needs additional citations for verification. (August 2010) 查找来源:“Chirp” – 新闻 · 报纸 · 书籍 · 学术 · JSTOR(2010 年 8 月)(了解如何以及何时删除此消息) |

线性调频波形;一个随着时间线性增加频率的正弦波
A chirp is a signal in which the frequency increases (up-chirp) or decreases (down-chirp) with time. In some sources, the term chirp is used interchangeably with sweep signal.[1] It is commonly applied to sonar, radar, and laser systems, and to other applications, such as in spread-spectrum communications (see chirp spread spectrum). This signal type is biologically inspired and occurs as a phenomenon due to dispersion (a non-linear dependence between frequency and the propagation speed of the wave components). It is usually compensated for by using a matched filter, which can be part of the propagation channel. Depending on the specific performance measure, however, there are better techniques both for radar and communication. Since it was used in radar and space, it has been adopted also for communication standards. For automotive radar applications, it is usually called linear frequency modulated waveform (LFMW).[2]
“啁啾”是一种信号,在这种信号中,频率随着时间增加(上啁啾)或减少(下啁啾)。在一些来源中,啁啾一词与扫频信号可以互换使用。它通常应用于声纳、雷达和激光系统,以及其他应用,如扩频通信(参见啁啾扩频)。这种信号类型受到生物启发,由于频散(频率和波动传播速度之间的非线性关系)而作为现象发生。通常使用匹配滤波器来补偿这一点,匹配滤波器可以是传播通道的一部分。然而,根据特定的性能指标,对于雷达和通信都有更好的技术。由于它在雷达和空间应用中被使用,因此也被采用于通信标准。在汽车雷达应用中,它通常被称为线性调频波形(LFMW)。
In spread-spectrum usage, surface acoustic wave (SAW) devices are often used to generate and demodulate the chirped signals. In optics, ultrashort laser pulses also exhibit chirp, which, in optical transmission systems, interacts with the dispersion properties of the materials, increasing or decreasing total pulse dispersion as the signal propagates. The name is a reference to the chirping sound made by birds; see bird vocalization.
在扩频应用中,表面声波(SAW)设备通常用于生成和解调啁啾信号。在光学中,超短激光脉冲也表现出啁啾,这在光传输系统中与材料的色散特性相互作用,随着信号传播增加或减少总脉冲色散。这个名字是指鸟类发出的啁啾声;参见鸟类发声。
Definitions 定义
[edit]The basic definitions here translate as the common physics quantities location (phase), speed (angular velocity), acceleration (chirpyness).
If a waveform is defined as:
这里的基本定义翻译为常见的物理量:位置(相位)、速度(角速度)、加速度(鸣叫)。如果波形定义为:
then the instantaneous angular frequency, ω, is defined as the phase rate as given by the first derivative of phase,
with the instantaneous ordinary frequency, f, being its normalized version:
那么瞬时角频率ω定义为相位的变化率,它由相位的一阶导数给出,瞬时普通频率 f 是其归一化版本:
Finally, the instantaneous angular chirpyness (symbol γ) is defined to be the second derivative of instantaneous phase or the first derivative of instantaneous angular frequency,
Angular chirpyness has units of radians per square second (rad/s2); thus, it is analogous to angular acceleration.
最后,即时角度啁啾度(符号 γ)被定义为瞬时相位的二阶导数或瞬时角频率的一阶导数, 角度啁啾度的单位是弧度每平方秒(rad/s 2 ),因此,它类似于角加速度。
The instantaneous ordinary chirpyness (symbol c) is a normalized version, defined as the rate of change of the instantaneous frequency:[3]
Ordinary chirpyness has units of square reciprocal seconds (s−2); thus, it is analogous to rotational acceleration.
瞬时普通啁啾度(符号 c)是一个标准化版本,定义为瞬时频率的变化率: [3] 普通啁啾度的单位是平方倒秒(s −2 );因此,它类似于旋转加速度。
Types 类型
[edit]Linear 线性
[edit]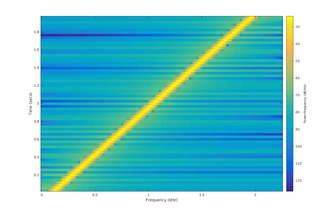
线性啁啾的声谱图。声谱图展示了频率随时间线性变化的速率,在这种情况下,从 0 到 7 kHz,每 2.3 秒重复一次。图的强度与信号在指示频率和时间上的能量内容成正比。
In a linear-frequency chirp or simply linear chirp, the instantaneous frequency varies exactly linearly with time:
where is the starting frequency (at time ) and is the chirp rate, assumed constant:
在线性频率啁啾或简单的线性啁啾中,瞬时频率 随时间线性变化: 其中 是起始频率(在时间 时)并且 是啁啾率,假设为常数:
Here, is the final frequency and is the time it takes to sweep from to .
这里, 是最终频率, 是从 扫描到 . 所需的时间
The corresponding time-domain function for the phase of any oscillating signal is the integral of the frequency function, as one expects the phase to grow like , i.e., that the derivative of the phase is the angular frequency .
任何振荡信号的相位对应的时域函数是频率函数的积分,因为人们期望相位像 增长,即相位的导数是角频率 。
For the linear chirp, this results in:
对于线性啁啾,这导致:
where is the initial phase (at time ). Thus this is also called a quadratic-phase signal.[4]
其中 是初始相位(在时间 时)。因此,这也称为二次相位信号。 [4]
The corresponding time-domain function for a sinusoidal linear chirp is the sine of the phase in radians:
线性频率调制的正弦波时域函数是相位的正弦值(弧度):
Exponential 指数的
[edit]
指数啁啾波形;一种随时间呈指数增加频率的正弦波

指数啁啾的声谱图。频率的指数变化速率作为时间的函数显示,在这种情况下,从接近 0 到每秒重复的 8 kHz。在这个声谱图中,还可以看到在峰值后频率回落到 6 kHz,可能是生成波形时所采用的特定方法的伪影。
In a geometric chirp, also called an exponential chirp, the frequency of the signal varies with a geometric relationship over time. In other words, if two points in the waveform are chosen, and , and the time interval between them is kept constant, the frequency ratio will also be constant.[5][6]
在几何调频信号中,也称为指数调频信号,信号的频率随时间以几何关系变化。换句话说,如果在波形中选择两个点, 和 ,并且它们之间的时间间隔 保持不变,那么频率比 也将保持不变。 [5] [6]
In an exponential chirp, the frequency of the signal varies exponentially as a function of time:
where is the starting frequency (at ), and is the rate of exponential change in frequency.
在指数扫频中,信号的频率作为时间的函数呈指数变化: 其中 是起始频率(在 ), 是频率的指数变化率。
Where is the ending frequency of the chirp (at ).
其中 是啁啾的结束频率(在 时)。
Unlike the linear chirp, which has a constant chirpyness, an exponential chirp has an exponentially increasing frequency rate.
与具有恒定调频特性的线性啁啾不同,指数啁啾具有呈指数增长的频率变化率。
The corresponding time-domain function for the phase of an exponential chirp is the integral of the frequency:
where is the initial phase (at ).
指数啁啾的相位对应的时域函数是频率的积分: 其中 是初始相位(在 时)。
The corresponding time-domain function for a sinusoidal exponential chirp is the sine of the phase in radians:
正弦指数啁啾的相应时域函数是相位的正弦(以弧度表示):
As was the case for the Linear Chirp, the instantaneous frequency of the Exponential Chirp consists of the fundamental frequency accompanied by additional harmonics.[citation needed]
与线性啁啾的情况一样,指数啁啾的瞬时频率由基频 及其附加谐波组成。 [citation needed]
Hyperbolic 双曲线
[edit]Hyperbolic chirps are used in radar applications, as they show maximum matched filter response after being distorted by the Doppler effect.[7]
双曲线啁啾在雷达应用中被使用,因为它们在经历多普勒效应的失真后显示出最大的匹配滤波器响应。 [7]
In a hyperbolic chirp, the frequency of the signal varies hyperbolically as a function of time:
在双曲线啁啾中,信号的频率随时间呈双曲线变化:
The corresponding time-domain function for the phase of an hyperbolic chirp is the integral of the frequency:
where is the initial phase (at ).
超幅线性啁啾的相位对应的时域函数是频率的积分: ,其中 是初始相位(在 时)。
The corresponding time-domain function for a sinusoidal hyperbolic chirp is the sine of the phase in radians:
正弦超双曲线啁啾的相应时域函数是相位(以弧度为单位)的正弦:
Generation 生成
[edit]A chirp signal can be generated with analog circuitry via a voltage-controlled oscillator (VCO), and a linearly or exponentially ramping control voltage.[8] It can also be generated digitally by a digital signal processor (DSP) and digital-to-analog converter (DAC), using a direct digital synthesizer (DDS) and by varying the step in the numerically controlled oscillator.[9] It can also be generated by a YIG oscillator.[clarification needed]
可以通过电压控制振荡器(VCO)和线性或指数逐渐增加的控制电压,使用模拟电路生成一个啁啾信号。 [8] 也可以通过数字信号处理器(DSP)和数模转换器(DAC)数字生成,使用直接数字合成器(DDS)并通过变更数控振荡器中的步幅。 [9] 还可以通过 YIG 振荡器生成。 [clarification needed]
Relation to an impulse signal
与脉冲信号的关系
[edit]
啁啾和脉冲信号及其(选定的)谱成分。底部给出了四个单色成分,不同频率的正弦波。波形中的红线表示相对于其他正弦波的相对相位移,源于啁啾特性。动画一步一步去除相位移(就像匹配过滤),当没有相对相位移剩余时,产生一个 sinc 脉冲。
A chirp signal shares the same spectral content with an impulse signal. However, unlike in the impulse signal, spectral components of the chirp signal have different phases,[10][11][12][13] i.e., their power spectra are alike but the phase spectra are distinct. Dispersion of a signal propagation medium may result in unintentional conversion of impulse signals into chirps (Whistler). On the other hand, many practical applications, such as chirped pulse amplifiers or echolocation systems,[12] use chirp signals instead of impulses because of their inherently lower peak-to-average power ratio (PAPR).[13]
啁啾信号与脉冲信号具有相同的频谱内容。然而,与脉冲信号不同,啁啾信号的频谱成分具有不同的相位,即它们的功率谱相似,但相位谱各不相同。信号传播介质的色散可能导致脉冲信号意外地转化为啁啾信号(Whistler)。另一方面,许多实际应用,如啁啾脉冲放大器或回声定位系统,使用啁啾信号而不是脉冲,因为它们具有固有的较低峰值与平均功率比(PAPR)。
Uses and occurrences 用途和发生情况
[edit]Chirp modulation 啁啾调制
[edit]Chirp modulation, or linear frequency modulation for digital communication, was patented by Sidney Darlington in 1954 with significant later work performed by Winkler in 1962. This type of modulation employs sinusoidal waveforms whose instantaneous frequency increases or decreases linearly over time. These waveforms are commonly referred to as linear chirps or simply chirps.
啾啾调制,或用于数字通信的线性频率调制,是在 1954 年由 Sidney Darlington 获得专利,1962 年 Winkler 进行了重要的后续工作。这种调制类型采用正弦波形,其瞬时频率随时间线性增加或减少。这些波形通常被称为线性啾啾或简单的啾啾。
Hence the rate at which their frequency changes is called the chirp rate. In binary chirp modulation, binary data is transmitted by mapping the bits into chirps of opposite chirp rates. For instance, over one bit period "1" is assigned a chirp with positive rate a and "0" a chirp with negative rate −a. Chirps have been heavily used in radar applications and as a result advanced sources for transmission and matched filters for reception of linear chirps are available.
因此,它们频率变化的速率称为啁啾速率。在二进制啁啾调制中,通过将比特映射到相反啁啾速率的啁啾中来传输二进制数据。例如,在一个比特周期内,“1”分配一个正速率 a 的啁啾,而“0”分配一个负速率 −a 的啁啾。啁啾在雷达应用中被广泛使用,因此可用于线性啁啾传输的先进源和用于接收的匹配滤波器已经可用。

(a) 在图像处理过程中,直接的周期性很少发生,而是会遇到透视中的周期性。(b) 像窗户内交替的暗空间和白色混凝土的亮空间这样的重复结构,向右“啁啾”(频率增加)。(c) 因此,图像处理的最佳拟合啁啾通常是投影啁啾。
Chirplet transform Chirplet 变换
[edit]Another kind of chirp is the projective chirp, of the form:
having the three parameters a (scale), b (translation), and c (chirpiness). The projective chirp is ideally suited to image processing, and forms the basis for the projective chirplet transform.[3]
另一种啁啾是投影啁啾,形式为: ,具有三个参数 a(比例)、b(平移)和 c(啁啾性)。投影啁啾非常适合图像处理,并构成了投影啁啾变换的基础。 [3]
Key chirp 关键啁啾
[edit]A change in frequency of Morse code from the desired frequency, due to poor stability in the RF oscillator, is known as chirp,[14] and in the R-S-T system is given an appended letter 'C'.
由于射频振荡器稳定性差,摩尔斯代码频率从期望频率的变化称为 chirp,在 R-S-T 系统中会附加一个字母 'C'。
See also 另见
[edit]- Chirp spectrum - Analysis of the frequency spectrum of chirp signals
啁啾频谱 - 啁啾信号频谱的分析 - Chirp compression - Further information on compression techniques
Chirp 压缩 - 有关压缩技术的更多信息 - Chirp spread spectrum - A part of the wireless telecommunications standard IEEE 802.15.4a CSS
啁啾扩频 - 无线电信标准 IEEE 802.15.4a CSS 的一部分 - Chirped mirror 啁啾镜
- Chirped pulse amplification
啁啾脉冲放大 - Chirplet transform - A signal representation based on a family of localized chirp functions.
Chirplet 变换 - 一种基于局部啁啾函数族的信号表示。 - Continuous-wave radar 连续波雷达
- Dispersion (optics) 色散(光学)
- Pulse compression 脉冲压缩
- Radio propagation § Measuring HF propagation
无线电传播 § 测量高频传播
References 参考文献
[edit]- ^ Weisstein, Eric W. "Sweep Signal". From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SweepSignal.html
Weisstein, Eric W. "Sweep Signal". 来源于 MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SweepSignal.html - ^ Lee, Tae-Yun; Jeon, Se-Yeon; Han, Junghwan; Skvortsov, Vladimir; Nikitin, Konstantin; Ka, Min-Ho (2016). "A Simplified Technique for Distance and Velocity Measurements of Multiple Moving Objects Using a Linear Frequency Modulated Signal". IEEE Sensors Journal. 16 (15): 5912–5920. Bibcode:2016ISenJ..16.5912L. doi:10.1109/JSEN.2016.2563458. S2CID 41233620.
- ^ Jump up to: a b Mann, Steve and Haykin, Simon; The Chirplet Transform: A generalization of Gabor's Logon Transform; Vision Interface '91.[1]
曼恩,史蒂夫与海金,西蒙;《Chirplet 变换:对 Gabor 的 Logon 变换的推广》;《视觉接口'91》。 [1] - ^ Easton, R.L. (2010). Fourier Methods in Imaging. Wiley. p. 703. ISBN 9781119991861. Retrieved 2014-12-03.
Easton, R.L. (2010). 图像中的傅里叶方法. Wiley. 第 703 页. ISBN 9781119991861. retrieved 2014-12-03 . - ^ Li, X. (2022-11-15), Time and Frequency Analysis Methods on GW Signals, retrieved 2023-02-10
李, X. (2022-11-15), GW 信号的时间和频率分析方法, 检索自 2023-02-10 - ^ Mamou, J.; Ketterling, J. A.; Silverman, R. H. (2008). "Chirp-coded excitation imaging with a high-frequency ultrasound annular array". IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 55 (2): 508–513. doi:10.1109/TUFFC.2008.670. PMC 2652352. PMID 18334358.
- ^ Yang, J.; Sarkar, T. K. (2006). "Doppler-invariant property of hyperbolic frequency modulated waveforms". Microwave and Optical Technology Letters. 48 (6): 1174–1179. doi:10.1002/mop.21573. S2CID 16476642.
- ^ "Chirp Signal - an overview | ScienceDirect Topics". www.sciencedirect.com. Retrieved 2023-02-10.
"Chirp Signal - 概述 | ScienceDirect 主题". www.sciencedirect.com. 获取于 2023-02-10 . - ^ Yang, Heein; Ryu, Sang-Burm; Lee, Hyun-Chul; Lee, Sang-Gyu; Yong, Sang-Soon; Kim, Jae-Hyun (2014). "Implementation of DDS chirp signal generator on FPGA". 2014 International Conference on Information and Communication Technology Convergence (ICTC). pp. 956–959. doi:10.1109/ICTC.2014.6983343. ISBN 978-1-4799-6786-5. S2CID 206870096.
- ^ "Chirped pulses". setiathome.berkeley.edu. Retrieved 2014-12-03.
"调制脉冲"。setiathome.berkeley.edu。检索于 2014-12-03 。 - ^ Easton, R.L. (2010). Fourier Methods in Imaging. Wiley. p. 700. ISBN 9781119991861. Retrieved 2014-12-03.
Easton, R.L. (2010). 图像中的傅里叶方法。 Wiley. 第 700 页. ISBN 9781119991861. 取自 2014-12-03 . - ^^ Jump up to: a b "Chirp Signals". dspguide.com. Retrieved 2014-12-03.
"Chirp Signals". dspguide.com. 已 retrieved 2014-12-03 . - ^ Jump up to: a b Nikitin, Alexei V.; Davidchack, Ruslan L. (2019). "Bandwidth is Not Enough: "Hidden" Outlier Noise and Its Mitigation". arXiv:1907.04186 [eess.SP].
Nikitin, Alexei V.; Davidchack, Ruslan L. (2019). "带宽不足:'隐藏'的离群噪声及其缓解". arXiv: 1907.04186 [ eess.SP]. - ^ The Beginner's Handbook of Amateur Radio By Clay Laster
业余无线电初学者手册 作者:克雷·拉斯特
External links 外部链接
[edit]维基媒体共享资源与 Chirp 相关的媒体。
在维基词典中查找 chirp,这本免费词典。
- Online Chirp Tone Generator (WAV file output)
在线鸣叫音调生成器(WAV 文件输出) - CHIRP Sonar on FishFinder
CHIRP 声纳在鱼探测器上 - CHIRP Sonar on FishFinder
CHIRP 声纳在鱼探测器上


















![{\displaystyle x(t)=\sin \left[\phi _{0}+2\pi \left({\frac {c}{2}}t^{2}+f_{0}t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e37a62aec3886518a3edefbdb75ad8ce54713d53)









![{\displaystyle x(t)=\sin \left[\phi _{0}+2\pi f_{0}\left({\frac {Tk^{\frac {t}{T}}}{\ln(k)}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c2a48e502c85f2b5718056269128ffef3a751be)


![{\displaystyle x(t)=\sin \left[\phi _{0}+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}}\ln \left(1-{\frac {f_{1}-f_{0}}{f_{1}T}}t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/394f4293ab0377aede2f9eda813093cead937b0f)
![{\displaystyle g=f\left[{\frac {a\cdot x+b}{c\cdot x+1}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a412682e5d49bc88d2da0f8ccea3024da8b075b)