Maximum length sequence 最大长度序列
A maximum length sequence (MLS) is a type of pseudorandom binary sequence.
最大长度序列(MLS)是一种伪随机二进制序列。
They are bit sequences generated using maximal linear-feedback shift registers and are so called because they are periodic and reproduce every binary sequence (except the zero vector) that can be represented by the shift registers (i.e., for length-m registers they produce a sequence of length 2m − 1). An MLS is also sometimes called an n-sequence or an m-sequence. MLSs are spectrally flat, with the exception of a near-zero DC term.
它们是使用最大线性反馈移位寄存器生成的比特序列,因此被称为,因为它们是周期性的,并且重现每个可以由移位寄存器表示的二进制序列(除了零向量)(即,对于长度为 m 的寄存器,它们产生长度为 2^m − 1 的序列)。MLS 有时也称为 n-sequence 或 m-sequence。MLS 的频谱平坦,近乎零的直流项除外。
These sequences may be represented as coefficients of irreducible polynomials in a polynomial ring over Z/2Z.
这些序列可以表示为在 Z/2Z 的多项式环中不可约多项式的系数。
Practical applications for MLS include measuring impulse responses (e.g., of room reverberation or arrival times from towed sources in the ocean[1]). They are also used as a basis for deriving pseudo-random sequences in digital communication systems that employ direct-sequence spread spectrum and frequency-hopping spread spectrum transmission systems, and in the efficient design of some fMRI experiments.[2]
MLS 的实际应用包括测量脉冲响应(例如,房间混响或来自海洋拖曳源的到达时间 [1] )。它们还作为基础,用于推导在采用直接序列扩频和频率跳变扩频传输系统的数字通信系统中使用的伪随机序列,以及一些 fMRI 实验的高效设计。 [2]
Generation 生成
[edit]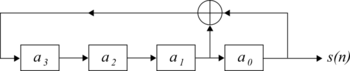
图 1:反馈移位寄存器长度为 4 时,寄存器 a 3 的下一个值由 a 0 和 a 1 的模 2 和决定。
MLS are generated using maximal linear-feedback shift registers. An MLS-generating system with a shift register of length 4 is shown in Fig. 1. It can be expressed using the following recursive relation:
MLS 是通过最大线性反馈移位寄存器生成的。图 1 显示了一个具有长度为 4 的移位寄存器的 MLS 生成系统。它可以用以下递归关系表示:
where n is the time index and represents modulo-2 addition. For bit values 0 = FALSE or 1 = TRUE, this is equivalent to the XOR operation.
其中 n 是时间索引, 表示模-2 加法。对于比特值 0 = FALSE 或 1 = TRUE,这相当于异或操作。
As MLS are periodic and shift registers cycle through every possible binary value (with the exception of the zero vector), registers can be initialized to any state, with the exception of the zero vector.
由于 MLS 是周期性的,而移位寄存器会循环遍历每一个可能的二进制值(零向量除外),寄存器可以初始化为任何状态,除了零向量。
Polynomial interpretation
多项式解释
[edit]A polynomial over GF(2) can be associated with the linear-feedback shift register. It has degree of the length of the shift register, and has coefficients that are either 0 or 1, corresponding to the taps of the register that feed the xor gate. For example, the polynomial corresponding to Figure 1 is .
在 GF(2)上的多项式可以与线性反馈移位寄存器相关联。它的阶数等于移位寄存器的长度,系数仅为 0 或 1,对应于供给异或门的寄存器抽头。例如,图 1 对应的多项式是 。
A necessary and sufficient condition for the sequence generated by a LFSR to be maximal length is that its corresponding polynomial be primitive.[3]
由 LFSR 生成的序列为最大长度的必要且充分条件是其对应的多项式是原始的。 [3]
Implementation 实施
[edit]MLS are inexpensive to implement in hardware or software, and relatively low-order feedback shift registers can generate long sequences; a sequence generated using a shift register of length 20 is 220 − 1 samples long (1,048,575 samples).
MLS 在硬件或软件中实现成本低廉,且相对低阶的反馈移位寄存器可以生成长序列;使用长度为 20 的移位寄存器生成的序列长度为 2 20 − 1 样本(1,048,575 样本)。
Properties of maximum length sequences
最大长度序列的属性
[edit]MLS have the following properties, as formulated by Solomon Golomb.[4]
MLS 具有以下特性,正如所罗门·戈隆布所制定的。 [4]
Balance property 平衡属性
[edit]The occurrence of 0 and 1 in the sequence should be approximately the same. More precisely, in a maximum length sequence of length there are ones and zeros. The number of ones equals the number of zeros plus one, since the state containing only zeros cannot occur.
序列中 0 和 1 的出现应该大致相同。更准确地说,在一个最大长度为 的序列中,有 个 1 和 个 0。1 的数量等于 0 的数量加 1,因为仅包含 0 的状态不能出现。
Run property 运行属性
[edit]A "run" is a sub-sequence of consecutive "1"s or consecutive "0"s within the MLS concerned. The number of runs is the number of such sub-sequences. [vague]
“运行”是相关 MLS 中连续“1”或连续“0”的子序列。运行的数量是此类子序列的数量。 [vague]
Of all the "runs" (consisting of "1"s or "0"s) in the sequence :
在序列中的所有“连续块”(由“1”或“0”组成):
- One half of the runs are of length 1.
一半的运行长度为 1。 - One quarter of the runs are of length 2.
四分之一的运行长度为 2。 - One eighth of the runs are of length 3.
八分之一的跑的长度为 3。 - ... etc. ... ... 等等 ...
Correlation property 相关性属性
[edit]The circular autocorrelation of an MLS is a Kronecker delta function[5][6] (with DC offset and time delay, depending on implementation). For the ±1 convention, i.e., bit value 1 is assigned and bit value 0 , mapping XOR to the negative of the product:
MLS 的循环自相关是一个克罗内克(delta)函数 [5] [6] (具有直流偏移和时间延迟,具体取决于实现)。对于±1 约定,即位值 1 被赋值为 ,位值 0 为 ,将 XOR 映射到乘积的负值:
where represents the complex conjugate and represents a circular shift.
其中 表示复共轭, 表示循环移位。
The linear autocorrelation of an MLS approximates a Kronecker delta.
MLS 的线性自相关近似于克罗内克δ。
Extraction of impulse responses
脉冲响应的提取
[edit]If a linear time invariant (LTI) system's impulse response is to be measured using a MLS, the response can be extracted from the measured system output y[n] by taking its circular cross-correlation with the MLS. This is because the autocorrelation of a MLS is 1 for zero-lag, and nearly zero (−1/N where N is the sequence length) for all other lags; in other words, the autocorrelation of the MLS can be said to approach unit impulse function as MLS length increases.
如果要使用 MLS 测量线性时不变(LTI)系统的脉冲响应,可以通过将测得的系统输出 y[n]与 MLS 进行循环互相关,提取响应。这是因为 MLS 的自相关在零延迟时为 1,其他所有延迟几乎为零(−1/N,其中 N 是序列长度);换句话说,随着 MLS 长度的增加,MLS 的自相关可以说接近单位脉冲函数。
If the impulse response of a system is h[n] and the MLS is s[n], then
如果系统的冲激响应是 h[n],而 MLS 是 s[n],那么
Taking the cross-correlation with respect to s[n] of both sides,
对两边关于 s[n] 的互相关进行处理,
and assuming that φss is an impulse (valid for long sequences)
并假设 φ ss 是一个冲激(适用于长序列)
Any signal with an impulsive autocorrelation can be used for this purpose, but signals with high crest factor, such as the impulse itself, produce impulse responses with poor signal-to-noise ratio. It is commonly assumed that the MLS would then be the ideal signal, as it consists of only full-scale values and its digital crest factor is the minimum, 0 dB.[7][8] However, after analog reconstruction, the sharp discontinuities in the signal produce strong intersample peaks, degrading the crest factor by 4-8 dB or more, increasing with signal length, making it worse than a sine sweep.[9] Other signals have been designed with minimal crest factor, though it is unknown if it can be improved beyond 3 dB.[10]
任何具有脉冲自相关的信号都可以用于此目的,但具有高峰值因子的信号,例如脉冲本身,会产生信噪比差的脉冲响应。通常认为,MLS 将是理想信号,因为它仅由满刻度值组成,其数字峰值因子为最小值 0 dB。 [7] [8] 然而,经过模拟重建后,信号中的尖锐不连续性会产生强烈的采样间隙峰值,使峰值因子降低 4-8 dB 或更多,并随着信号长度增加而恶化,变得比正弦扫描更糟。 [9] 其他信号已经设计为具有最小峰值因子,但尚不清楚是否可以将其改进到超过 3 dB。 [10]
Relationship to Hadamard transform
与阿达玛变换的关系
[edit]Cohn and Lempel[11] showed the relationship of the MLS to the Hadamard transform. This relationship allows the correlation of an MLS to be computed in a fast algorithm similar to the FFT.
Cohn 和 Lempel [11] 显示了 MLS 与 Hadamard 变换之间的关系。这个关系允许以类似于 FFT 的快速算法计算 MLS 的相关性。
See also 另见
[edit]- Barker code 巴克码
- Complementary sequences 互补序列
- Federal Standard 1037C 联邦标准 1037C
- Frequency response 频率响应
- Gold code 金码
- Impulse response 冲激响应
- Polynomial ring 多项式环
References 参考文献
[edit]- Golomb, Solomon W.; Guang Gong (2005). Signal Design for Good Correlation: For Wireless Communication, Cryptography, and Radar. Cambridge University Press. ISBN 978-0-521-82104-9.
Golomb, Solomon W.; Guang Gong (2005). 良好相关性的信号设计:用于无线通信、密码学和雷达。剑桥大学出版社。ISBN 978-0-521-82104-9。
- ^ Gemba, Kay L.; Vazquez, Heriberto J.; Fialkowski, Joseph; Edelmann, Geoffrey F.; Dzieciuch, Matthew A.; Hodgkiss, William S. (October 2021). "A performance comparison between m-sequences and linear frequency-modulated sweeps for the estimation of travel-time with a moving source". The Journal of the Acoustical Society of America. 150 (4): 2613–2623. Bibcode:2021ASAJ..150.2613G. doi:10.1121/10.0006656. PMID 34717519. S2CID 240355915.
- ^ Buracas GT, Boynton GM (July 2002). "Efficient design of event-related fMRI experiments using M-sequences". NeuroImage. 16 (3 Pt 1): 801–13. doi:10.1006/nimg.2002.1116. PMID 12169264. S2CID 7433120.
- ^ "Linear Feedback Shift Registers-Implementation, M-Sequence Properties, Feedback Tables"[1], New Wave Instruments (NW), Retrieved 2013.12.03.
"线性反馈移位寄存器 - 实现,M 序列特性,反馈表" [1],新波仪器 (NW),检索于 2013 年 12 月 03 日。 - ^ Golomb, Solomon W. (1967). Shift register sequences. Holden-Day. ISBN 0-89412-048-4.
戈隆布,所罗门·W.(1967)。移位寄存器序列。霍尔登-戴公司。ISBN 0-89412-048-4。 - ^ Jacobsen, Finn; Juhl, Peter Moller (2013-06-04). Fundamentals of General Linear Acoustics. John Wiley & Sons. ISBN 978-1118636176.
A maximum-length sequence is a binary sequence whose circular autocorrelation (except for a small DC-error) is a delta function.
雅各布森, 芬; 朱尔, 彼得·摩勒 (2013-06-04)。一般线性声学基础。约翰·威利父子公司。ISBN 978-1118636176。最大长度序列是一个二进制序列,其循环自相关(除了一个小的直流误差)是一个狄拉克函数。 - ^ Sarwate, D. V.; Pursley, M. B. (1980-05-01). "Crosscorrelation properties of pseudorandom and related sequences". Proceedings of the IEEE. 68 (5): 593–619. doi:10.1109/PROC.1980.11697. ISSN 0018-9219. S2CID 6179951.
Sarwate, D. V.; Pursley, M. B. (1980-05-01). “伪随机及相关序列的互相关特性”。《IEEE 汇刊》。68 (5): 593– 619. doi: 10.1109/PROC.1980.11697. ISSN 0018-9219. S2CID 6179951. - ^ "A Little MLS (Maximum-Length Sequence) Tutorial | dspGuru.com". dspguru.com. Retrieved 2016-05-19.
its RMS and peak values are both X, making its crest factor (peak/RMS) equal to 1, the lowest it can get.
《小型 MLS(最大长度序列)教程 | dspGuru.com》。dspguru.com。检索到 2016-05-19 。它的均方根值和峰值均为 X,使其波峰因子(峰值/均方根值)等于 1,这是它可以达到的最低值。 - ^ "Other Electro-Acoustical Measurement Techniques". www.clear.rice.edu. Retrieved 2016-05-19.
The crest factor for MLS is very close to 1, so it makes sense to use this kind of input signal when we need a high signal-to-noise ratio for our measurement
"其他电声测量技术". www.clear.rice.edu. 查阅于 2016-05-19 。MLS 的峰值因子非常接近 1,因此当我们需要高信噪比的测量时,使用这种输入信号是合理的。 - ^ Chan, Ian H. "Swept Sine Chirps for Measuring Impulse Response" (PDF). thinksrs.com. Retrieved 2016-05-19.
Maximum-length sequence (MLS) theoretically fits the bill because it has a mathematical crest factor of 0dB, the lowest crest factor possible. However, in practice, the sharp transitions and bandwidth-limited reproduction of the signal result in a crest factor of about 8dB
陈, 伊恩 H. "用于测量脉冲响应的扫频正弦波" (PDF). thinksrs.com. 检索于 2016-05-19 。最大长度序列 (MLS) 在理论上符合要求,因为它具有 0dB 的数学波峰因子,这是可能的最低波峰因子。然而,在实践中,信号的急剧转换和带宽限制的再现导致波峰因子约为 8dB。 - ^ Friese, M. (1997-10-01). "Multitone signals with low crest factor" (PDF). IEEE Transactions on Communications. 45 (10): 1338–1344. doi:10.1109/26.634697. ISSN 0090-6778.
- ^ Cohn, M.; Lempel, A. (January 1977). "On Fast M-Sequence Transforms". IEEE Trans. Inf. Theory. 23 (1): 135–7. doi:10.1109/TIT.1977.1055666.
External links 外部链接
[edit]- Bristow-Johnson, Robert. "A Little MLS Tutorial". — Short on-line tutorial describing how MLS is used to obtain the impulse response of a linear time-invariant system. Also describes how nonlinearities in the system can show up as spurious spikes in the apparent impulse response.
布里斯托-约翰逊,罗伯特。《小型 MLS 教程》。——在线简短教程,描述了如何使用 MLS 获得线性时不变系统的脉冲响应。还描述了系统中的非线性如何表现为明显脉冲响应中的虚假尖峰。 - Hee, Jens. "Impulse response measurement using MLS" (PDF). — Paper describing MLS generation. Contains C-code for MLS generation using up to 18-tap-LFSRs and matching Hadamard transform for impulse response extraction.
嘿,延斯。“使用 MLS 的脉冲响应测量”(PDF)。——描述 MLS 生成的论文。包含用于 MLS 生成的 C 代码,使用多达 18 个抽头的 LFSR 和匹配 Hadamard 变换进行脉冲响应提取。 - Schäfer, Magnus (October 2012). "Aachen Impulse Response Database". Institute of Communication Systems and Data Processing, RWTH Aachen University. V1.4. A (binaural) room impulse response database generated by means of maximum length sequences.
Schäfer, Magnus (2012 年 10 月). "亚琛冲击响应数据库". 通信系统与数据处理研究所, 亚琛工业大学. V1.4. 通过最大长度序列生成的(双耳)房间冲击响应数据库。 - "Efficient Shift Registers, LFSR Counters, and Long Pseudo-Random Sequence Generators — Obsolete" (PDF). Xilinx. July 1996. XAPP052 v1.1. — Implementing lfsr's in FPGAs includes listing of taps for 3 to 168 bits
“高效移位寄存器、LFSR 计数器和长伪随机序列生成器 — 废弃” (PDF)。 Xilinx。1996 年 7 月。 XAPP052 v1.1。 — 在 FPGA 中实现 lfsr 包括 3 到 168 位的抽头列表。

![{\displaystyle {\begin{cases}a_{3}[n+1]=a_{0}[n]+a_{1}[n]\\a_{2}[n+1]=a_{3}[n]\\a_{1}[n+1]=a_{2}[n]\\a_{0}[n+1]=a_{1}[n]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f938524a53e278703e9b8b19db795caf70942202)







![{\displaystyle R(n)={\frac {1}{N}}\sum _{m=1}^{N}s[m]\,s^{*}[m+n]_{N}={\begin{cases}1&{\text{if }}n=0,\\-{\frac {1}{N}}&{\text{if }}0<n<N.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c3c733c7432da2ff2c5dcb646712fad86a95194)

![{\displaystyle [m+n]_{N}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0b82c886262175ab1bb25fc393a865b5fd4e8e8)
![{\displaystyle y[n]=(h*s)[n].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0da0dbee41ee90fcd53431e697b7212ac49730)
![{\displaystyle {\phi }_{sy}=h[n]*{\phi }_{ss}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46b93ff2da18e3495897a7acddd25993963c162a)
![{\displaystyle h[n]={\phi }_{sy}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbd795d98fc94486378d66f18843cfa4b0c10bd8)