Around 2,500 years ago humankind began to recognize that our planet is round—although a few “flat Earth” supporters still deny this today. The shape of our universe is not clear, however. Previous studies have suggested that the cosmos probably has a fairly simple shape, such as the three-dimensional equivalent of a spherical surface or a plane. But this view may be wrong, according to cosmologists from the Collaboration for Observations, Models and Predictions of Anomalies and Cosmic Topology (COMPACT). In a paper published in April 2024, they found that the shape of the universe could be significantly more complex than previously assumed.
大约 2500 年前,人类开始认识到我们的地球是圆的--尽管少数 "平地 "支持者至今仍否认这一点。然而,我们宇宙的形状并不清晰。以前的研究表明,宇宙可能具有相当简单的形状,比如相当于球面或平面的三维形状。但是,根据反常现象和宇宙拓扑观测、模型和预测合作组织(COMPACT)的宇宙学家们的研究,这种观点可能是错误的。在 2024 年 4 月发表的一篇论文中,他们发现宇宙的形状可能比之前假设的要复杂得多。
Earth also appears flat at first glance. This is because its radius is so large that the surface’s curvature is barely perceptible. To prove it’s a sphere, you would just have to start walking. If you were to move straight ahead without ever turning—crossing over mountains and oceans—you would inevitably return to the start at some point.
地球乍一看也是平的。这是因为它的半径太大,表面的曲率几乎感觉不到。要证明它是一个球体,你只需开始行走。如果你一直向前走,不转弯,越过高山和海洋,你将不可避免地在某一时刻回到起点。
Cosmologists collect similar clues to determine the shape of the universe. They could send a spaceship out to traverse the cosmos. Instead they peer into the night sky and examine traces of the oldest light that reaches us from the depths of the cosmos. This radiation was created around 300,000 years after the big bang. Although photons had existed even before that, matter was so densely packed into what was then a small universe that the light quanta had no chance of traveling freely. Eventually, however, the universe cooled down to such an extent that it became transparent. The photons were able to spread freely through space—and still do today.
宇宙学家收集类似的线索来确定宇宙的形状。他们可以派出宇宙飞船穿越宇宙。相反,他们窥探夜空,研究从宇宙深处到达我们这里的最古老光线的痕迹。这种辐射是在宇宙大爆炸后大约 30 万年产生的。虽然光子在此之前就已经存在,但当时的小宇宙中物质非常密集,光量子根本无法自由传播。然而,宇宙最终冷却到了透明的程度。光子得以在太空中自由传播,直到今天依然如此。
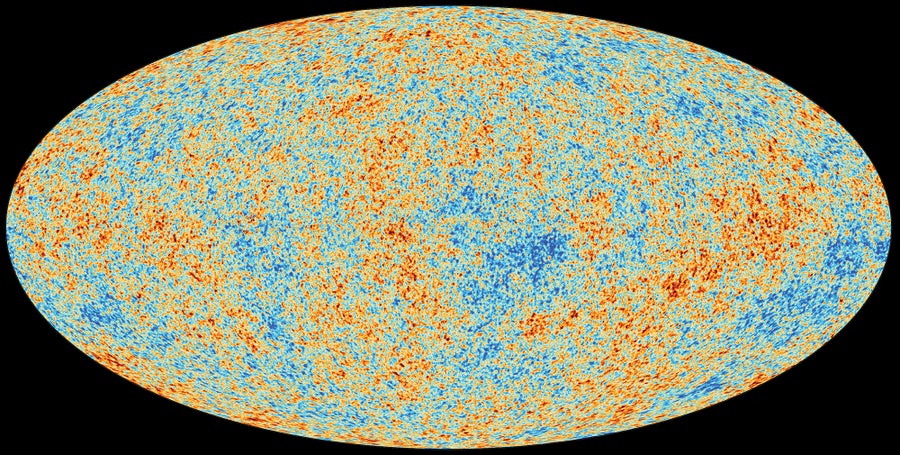
Mapping out the oldest light in the universe—the so-called cosmic microwave background—offers clues to the shape of the cosmos.
ESA and Planck Collaboration
绘制出宇宙中最古老的光线--所谓的宇宙微波背景--提供了有关宇宙形状的线索。
Photons from this early time in the universe reach us as cosmic background radiation. Approximately the same pattern of old light comes from every corner of the universe. This radiation provides clues to the shape of the universe. If, for example, the curvature of the universe were to change at one point, the cosmic background radiation would not be as homogeneous as we observe it. Experts therefore assume that the universe is either curved in the same way everywhere—or is completely flat.
来自宇宙早期的光子以宇宙背景辐射的形式出现在我们面前。来自宇宙每个角落的古老光线的模式大致相同。这种辐射提供了宇宙形状的线索。例如,如果宇宙的曲率在某一点上发生了变化,那么宇宙背景辐射就不会像我们观测到的那样均匀。因此,专家们假定宇宙要么到处都是同样的曲率,要么就是完全平坦的。
A Wealth of Possibilities
丰富的可能性
It is difficult to imagine the universe having no curvature or constant curvature. That’s why it helps to use two-dimensional examples. In this analogy, to fit the homogeneous patterns of cosmic background radiation, the universe can be actually flat like a flat sheet of paper (no curvature), correspond to the three-dimensional counterpart of a spherical surface (positive curvature) or form a kind of three-dimensional saddle surface (negative curvature). In all three cases, the curvature is constant everywhere.
很难想象宇宙没有曲率或曲率恒定。这就是为什么使用二维例子会有帮助。在这个类比中,为了符合宇宙背景辐射的均匀模式,宇宙可以像一张平纸一样实际上是平的(无曲率),也可以对应于球面的三维对应面(正曲率),或者形成一种三维鞍面(负曲率)。在这三种情况下,曲率在任何地方都是恒定的。
But this still does not reveal what the universe as a whole looks like. For example, space could be curved in the same way everywhere and still have a hole. The mathematical discipline of topology can be used to differentiate between such cases. Topologists classify geometric figures according to rough categories, such as the number of holes in them, in order to create a catalog of shapes. Cosmologists aim to assign one of these shapes to the universe.
但这仍然无法揭示宇宙的整体面貌。例如,空间可以在任何地方以同样的方式弯曲,但仍然会有一个洞。拓扑学这门数学学科可以用来区分这种情况。拓扑学家根据几何图形的粗略分类,比如其中的洞的数量,对几何图形进行分类,从而建立一个形状目录。宇宙学家的目标是将其中的一种形状赋予宇宙。
As mathematicians have been able to prove, there are an infinite number of different categories (topologies) of curved three-dimensional surfaces. So if spacetime really is saddle-shaped or spherical, then there are theoretically any number of shapes that the universe can take on, each of which is very different from the other. Cosmological observations to date, however, point to a flat universe without curvature. If true, this insight narrows the search for the topology of the universe: as mathematician Grigori Perelman deduced in 2003, the catalog of flat three-dimensional surfaces is very small, with only 18 different categories.
数学家已经证明,三维曲面有无数种不同的类别(拓扑结构)。因此,如果时空真的是马鞍形或球形的,那么理论上宇宙可以呈现出任意多种形状,每种形状都截然不同。然而,迄今为止的宇宙学观测表明,宇宙是平坦的,没有曲率。如果这一观点属实,那么对宇宙拓扑学的探索就缩小了范围:正如数学家格里高利-佩雷尔曼(Grigori Perelman)在 2003 年推断的那样,平面三维表面的目录非常小,只有 18 个不同的类别。
One of 18 Shapes 18种形状之一
The shape of the universe therefore presumably corresponds to one of these 18 shapes. One is the three-dimensional analog of a sheet of paper. Our cosmos could also have holes, however. Among the 18 topologies, the three-dimensional equivalent of a donut surface is a so-called torus.
因此,宇宙的形状大概对应于这 18 种形状中的一种。一种是纸张的三维类似物。不过,我们的宇宙也可能有洞。在这 18 种拓扑结构中,甜甜圈表面的三维等价物是所谓的环。
Although a donut appears curved at first glance, it turns out that this shape is actually flat. This is because a donut shape can be created using a (very flexible) sheet of paper. To do this, you first stick the opposite long sides of the sheet together, creating an elongated tube. Then you bend the tube and bring the two openings together.
虽然甜甜圈乍一看是弧形的,但实际上它是平面的。这是因为甜甜圈的形状可以用一张(非常柔软的)纸来制作。要做到这一点,首先要将纸片相对的长边粘在一起,形成一个拉长的管子。然后弯曲管子,将两个开口合在一起。
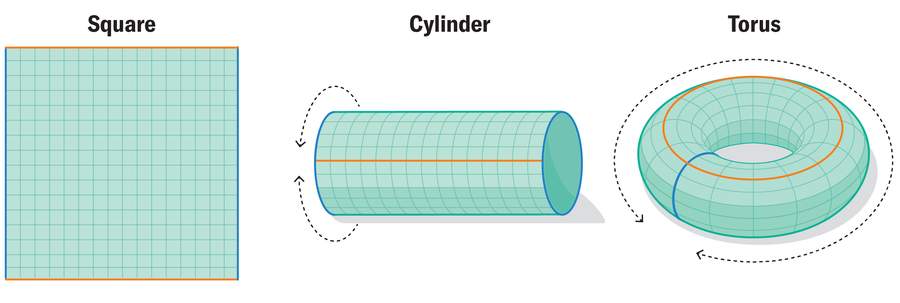
When viewed as a whole, a torus can be described as a flat, rectangular area—or folded and rolled into a donut shape.
Lucy Reading-Ikkanda
从整体上看,环状体可以被描述为一个扁平的矩形区域,也可以被折叠卷成一个甜甜圈形状。
This construction has many advantages. For example, if you want to describe the movement of an ant on a donut, it is usually easier to imagine the rectangular sheet of paper. The insect walks around on the piece of paper and as soon as it crosses an edge, it reenters the opposite side of the sheet—as in the popular mobile game Snake from the 2000s. If the ant moves in a straight line, it will inevitably end up back at the start at some point.
这种结构有很多优点。例如,如果你想描述一只蚂蚁在甜甜圈上的运动,想象一下矩形纸片通常会更容易。昆虫在纸片上走来走去,一旦越过边缘,就会重新进入纸片的另一侧--就像 2000 年代流行的手机游戏《贪吃蛇》中那样。如果蚂蚁沿直线运动,那么它最终必然会回到起点。
You can create a three-dimensional torus in the same way by using a three-dimensional cuboid instead of a rectangular sheet of paper. In this case, you also deform it so that opposite sides of the cuboid are glued together.
用三维立方体代替长方形纸张,也可以用同样的方法创建三维环。在这种情况下,您还可以对它进行变形,使长方体的对边粘在一起。
A Donut Universe with Loops
环形甜甜圈宇宙
If our universe were torus-shaped, this would have tangible consequences. If we were to shine a flashlight into the sky, for example, this light would theoretically reach us again at some point—just as the ant on the sheet of paper always returns to its starting point. Such loops exist in most of the 18 different topologies. These are trajectories that return to their starting point. At first glance, however, the loops do not seem to correspond to our observations. If light were to periodically pass through space, we would have to see several copies of the universe in the night sky.
如果我们的宇宙是环形的,这就会产生切实的后果。例如,如果我们用手电筒向天空照射,理论上这束光会在某一点再次到达我们这里--就像纸上的蚂蚁总是回到它的起点一样。在 18 种不同的拓扑结构中,大部分都存在这种循环。这些都是返回起点的轨迹。然而,乍一看,这些循环似乎与我们的观测结果并不相符。如果光线周期性地穿过太空,我们就必须在夜空中看到宇宙的多个副本。
Still, this fact does not exclude all topologies with loops. We could live in a universe so large that light has not yet had enough time to traverse it and return. Perhaps in several billion years, humans (or other beings) will have the pleasure of seeing a night sky that contains numerous images of the universe.
尽管如此,这一事实并不排除所有带有环路的拓扑结构。我们可能生活在一个如此巨大的宇宙中,以至于光还没有足够的时间穿越宇宙并返回。也许在几十亿年后,人类(或其他生物)将有幸看到包含无数宇宙图像的夜空。
But even such huge loops would leave traces today. For example, the shape of the cosmos would have influenced how matter and light interacted with each other in the early universe. If the universe had holes—and therefore also loops—this fact should be reflected in the data of the cosmic background radiation.
但是,即使是如此巨大的环路也会在今天留下痕迹。例如,宇宙的形状会影响早期宇宙中物质和光的相互作用。如果宇宙有洞,因此也有环,那么宇宙背景辐射的数据就应该反映出这一事实。
Yet in searches from the 2000s and 2010s, experts found nothing. Most cosmologists have therefore assumed that the universe had a fairly simple structure. Research into the shape of the universe stalled—at least until COMPACT launched in 2022.
然而,在 2000 年代和 2010 年代的搜索中,专家们一无所获。因此,大多数宇宙学家都认为宇宙的结构相当简单。对宇宙形状的研究停滞不前--至少在 2022 年 COMPACT 发射之前是如此。
Significantly More Possibilities Than Expected
可能性大大高于预期
The COMPACT team compared the latest data on cosmological background radiation with various topologies of the universe—and came up with surprising results in its first publication. Among other things, the researchers discovered that previous work had ignored many variants of the individual topologies. In other words, researchers may have previously missed other forms that could describe our cosmos. The collaboration was also able to show that the missing evidence for loops in the cosmic background radiation is far less restrictive than previously assumed. In addition to loops, there could be other traces in the cosmic background radiation that point to complicated topologies. Future work will explore what exactly these shapes could be.
COMPACT 小组将宇宙背景辐射的最新数据与宇宙的各种拓扑结构进行了比较,并在首次发表的论文中得出了令人惊讶的结果。其中,研究人员发现以前的工作忽略了各种拓扑结构的许多变体。换句话说,研究人员以前可能忽略了其他可以描述我们宇宙的形式。合作研究还表明,宇宙背景辐射中缺少的循环证据远没有之前假设的那么严格。除了环路之外,宇宙背景辐射中还可能存在其他指向复杂拓扑结构的踪迹。未来的工作将探索这些形状究竟是什么。
The researchers backed up their arguments using three concrete example topologies of flat space: an ordinary torus and two variations of it in which the faces of the cuboid are twisted before being glued together. All three have holes. For the ordinary torus, COMPACT confirmed earlier conclusions: if our universe is torus-shaped, the loops must be so large that light has not yet been able to reach us. But the surprise was that this same idea may not apply to the modified shapes. The collaboration’s calculations show that loops of these shapes could also be significantly shorter than what was assumed from the previous data. Because of the many twists, the universe could contain copies of itself that might look different from the original, making them less easy to spot in maps of the cosmic microwave background.
研究人员用三个具体的平面空间拓扑实例来支持他们的论点:一个普通的环面和两个变体,在这两个变体中,长方体的面在被粘合在一起之前是扭曲的。这三种拓扑结构都有孔洞。对于普通的环形空间,COMPACT 证实了之前的结论:如果我们的宇宙是环形的,那么环形空间一定非常大,以至于光还无法到达我们这里。但令人惊讶的是,同样的想法可能并不适用于修改过的形状。合作者的计算显示,这些形状的环也可能比之前数据假设的要短得多。由于存在许多曲折,宇宙可能包含了自身的拷贝,这些拷贝看起来可能与原来的不同,从而使它们在宇宙微波背景图中不那么容易被发现。
Taken together, the COMPACT team’s findings show that the universe could look far more complicated than previously assumed. And that would have far-reaching consequences. The shape of our cosmos is not just an academic question. The topology of spacetime was presumably determined by the quantum processes that took place shortly after the big bang. If we knew more about the shape of the universe, we could—potentially—learn more about the complex processes that took place at its beginning.
综合来看,COMPACT 小组的研究结果表明,宇宙可能比之前假设的要复杂得多。这将产生深远的影响。宇宙的形状不仅仅是一个学术问题。时空的拓扑结构可能是由大爆炸后不久发生的量子过程决定的。如果我们对宇宙的形状有更多的了解,我们就有可能对宇宙诞生之初的复杂过程有更多的了解。
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.
本文原载于 Spektrum der Wissenschaft,经授权转载。

