Introduction  介绍

Ocean surface waves have been observed to penetrate tens and, at times, hundreds of kilometres into the sea-ice-covered ocean (Reference KohoutKohout and others, 2014). The waves cause the ice to bend and flex. The ice can only endure a certain degree of flexure before it fractures into floes with diameters on the order of local wavelengths (Reference Langhorne, Squire and FoxLanghorne and others, 1998). In this way, waves regulate maximum floe sizes. Simultaneously, the presence of ice cover attenuates the waves. Waves therefore retain the intensity to fracture the ice for a finite distance only. Moreover, ice cover filters the wave spectrum preferentially towards low frequencies, so that wavelengths and, consequently, maximum floe sizes generally increase with distance travelled (Reference SquireSquire and Moore, 1980), until winds, currents and further waves reconfigure the simple arrangement.
海洋表面波被观察到可以渗透到海冰覆盖的海洋中数十公里，有时甚至数百公里（Kohout et al., 2014）。这些波浪使冰层弯曲和变形。冰层只能承受一定程度的弯曲，之后会断裂成直径与局部波长相当的冰块（Langhorne et al., 1998）。通过这种方式，波浪调节最大冰块的大小。同时，冰盖的存在会衰减波浪。因此，波浪仅在有限的距离内保持足以破裂冰层的强度。此外，冰盖优先过滤波谱向低频率，因此波长和最大冰块大小通常随着传播距离的增加而增加（Squire and Moore, 1980），直到风、洋流和进一步的波浪重新配置这种简单的排列。

Wave attenuation is typically modelled as an accumulation of partial wave reflections and transmissions by floes (see Reference BennettsBennetts and Squire, 2012, and references therein). Comparatively few fracture models exist. Those that do exist are based on wave-induced flexural motion of the ice, resulting in strains that exceed a threshold (e.g. Reference Langhorne, Squire, Fox and forLanghorne and others, 2001).
波浪衰减通常被建模为浮冰对部分波反射和透射的累积（见 Bennetts 和 Squire，2012 年及其中的参考文献）。现有的裂缝模型相对较少。现有的模型基于波浪引起的冰的弯曲运动，导致应变超过阈值（例如，Langhorne 等，2001 年）。

Until recently, wave attenuation and ice fracture models have been independent of one another. Attenuation models consider the floe size distribution to be known. Fracture models consider the distribution of wave energy to be known. However, wave attenuation and ice fracture are coupled via the floe size distribution. The rate of wave attenuation depends on the floe size distribution, which is regulated by wave-induced fracture. Fracture depends on the local wave energy, which is controlled by wave attenuation imposed by the ice cover (Reference KohoutKohout and Meylan, 2008).
直到最近，波衰减和冰裂模型一直是相互独立的。衰减模型认为浮冰大小分布是已知的。裂纹模型认为波能量分布是已知的。然而，波衰减和冰裂是通过浮冰大小分布耦合在一起的。波衰减的速率依赖于浮冰大小分布，而浮冰大小分布又受到波引起的裂纹的调节。裂纹依赖于局部波能量，而局部波能量又受到冰盖施加的波衰减的控制（Kohout and Meylan, 2008）。

Reference Dumont, Kohout and BertinoDumont and others (2011) and Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013a,Reference Williams, Bennetts, Squire, Dumont and Bertinob) developed a wave-ice interaction model (WIM), in which wave attenuation and ice fracture are coupled processes. The WIM predicts the distribution of wave energy and the resulting floe size distribution simultaneously, given an incident wave forcing from the open ocean and properties of the ice cover.
Dumont 等人（2011）和 Williams 等人（2013a,b）开发了一个波浪-冰相互作用模型（WIM），在该模型中，波浪衰减和冰裂是耦合过程。WIM 在给定来自开放海洋的入射波强迫和冰盖特性的情况下，同时预测波浪能量的分布和由此产生的浮冰大小分布。

Reference Dumont, Kohout and BertinoDumont and others (2011) and Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013a,Reference Williams, Bennetts, Squire, Dumont and Bertinob) designed the WIM to link wave and sea-ice model components of large-scale operational ice-ocean forecasting models. The WIM is nested in regions of operational interest in the large-scale models using refined spatial and temporal grids. The WIM then provides prognostic information regarding the floe size distribution and wave activity in the ice-covered ocean, potentially leading to more accurate forecasts for the safety of offshore engineering activities.
Dumont 等人 (2011) 和 Williams 等人 (2013a,b) 设计了 WIM，以连接大规模操作性冰-海洋预报模型的波浪和海冰模型组件。WIM 在大规模模型中使用精细的空间和时间网格嵌套在操作性关注区域。然后，WIM 提供有关冰盖海洋中浮冰大小分布和波浪活动的预报信息，可能导致对离岸工程活动安全性的更准确预测。

More generally, the WIM provides an opportunity to integrate prognostic wave and floe size information into oceanic general circulation models (OGCMs) used for climate studies, and here considered to contain wave and sea-ice model components. The information will improve the accuracy of existing models of floe-size-dependent processes in the vicinity of the ice edge, such as form drag (Reference Tsamados, Feltham, Schroeder and FloccoTsamados and others, 2014), and promote development of new models of wave- and floe-size-dependent processes, such as accelerated melt of floes due to wave overwash (Reference MassomMassom and Stammerjohn, 2010).
更一般地说，WIM 提供了将预报波浪和浮冰大小信息整合到用于气候研究的海洋大气环流模型（OGCMs）中的机会，并在这里考虑包含波浪和海冰模型组件。这些信息将提高现有浮冰大小依赖过程模型的准确性，特别是在冰缘附近的过程，如形状阻力（Tsamados 等，2014），并促进新模型的发展，这些模型涉及波浪和浮冰大小依赖的过程，例如由于波浪冲刷导致的浮冰加速融化（Massom 和 Stammerjohn，2010）。

Subgridding incurs a large computational cost. It is therefore not an appropriate method to implement the WIM on circumpolar or global scales. An alternative numerical implementation is proposed here, for a modified version of the WIM. The new method does not involve subgrid spatial or temporal discretizations. Instead, the floe size distribution and the rate of attenuation are balanced in the cell.
子网格化会产生较大的计算成本。因此，这并不是在极地或全球范围内实施 WIM 的合适方法。这里提出了一种替代的数值实现，用于 WIM 的修改版本。新方法不涉及子网格空间或时间离散化。相反，冰块大小分布和衰减速率在单元中保持平衡。

Application of the new scheme to an idealized version of the modified WIM is presented. Results are validated by comparison to results produced by the method of Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b).
对修改后的 WIM 理想化版本应用新方案的结果进行了展示。结果通过与 Williams 等人（2013b）的方法产生的结果进行比较来验证。

Model Description  模型描述

Consider a transect of the ocean surface containing ice cover. Points on the transect are defined by the coordinate x 6 (0, L). The transect represents a single cell in an OGCM. The time frame under consideration, t ∊ (0, T), is equivalent to a single time step in the OGCM. For climate models L ∼ 50 km and T ∼ 1 hour. The sea-ice model component of the OGCM is assumed to provide an average ice thickness, h, and concentration of the ice cover, c. (Contemporary sea-ice models distribute ice thickness over multiple categories.) The average ice thickness h = 0.5 m and concentration c = 0.75 are prescribed for the idealized model results presented later.
考虑一个包含冰盖的海洋表面横断面。横断面上的点由坐标 x 6 (0, L) 定义。该横断面代表 OGCM 中的一个单元格。考虑的时间框架 t ∊ (0, T), 相当于 OGCM 中的一个时间步长。对于气候模型，L ∼ 50 km 和 T ∼ 1 小时。OGCM 的海冰模型组件假定提供平均冰厚度 h, 和冰盖浓度 c。（当代海冰模型将冰厚度分布在多个类别中。）理想化模型结果中规定的平均冰厚度 h = 0.5 m 和浓度 c = 0.75。

Let the wave energy density spectrum at point x and time t be denoted S(w;x,t), where ω is angular frequency. The domain x ∊ (0, L) is considered to be free of waves initially. An incident wave spectrum is prescribed at the left-hand end of the domain, x = 0. Incident wave forcing is steady over the time interval considered.
在点x和时间t处的波能量密度谱记作S(w;x,t), 其中ω是角频率。域x ∊ (0, L) 被认为最初是没有波的。在域的左端x = 0 处规定了入射波谱。入射波的强迫在考虑的时间区间内是稳定的。

The incident spectrum is transported through the transect according to the energy-balance equation
事件光谱通过横断面根据能量平衡方程进行传输

(1)

The quantity cg is the group velocity of the waves. Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b) provide numerical evidence that ice fracture predicted by the WIM is insensitive to wave dispersion. Although the finding is not conclusive, for simplicity dispersion is neglected for the present application, i.e. a constant value of cg is used in the transport equation. Further, it is assumed that the wave spectrum travels the length of the transect in the time frame, i.e. cg = L/T, thus alleviating the need to specify a value for cg.The quantity α(w;x,t) is the attenuation coefficient, i.e. the exponential attenuation rate of wave energy per meter. The expression α = ca/{d) is used here, where d denotes floe diameter, ⟨·⟩ denotes the mean of the included quantity and a(ω, h) is the attenuation rate per floe, calculated using the model of Reference BennettsBennetts and Squire (2012). The attenuation coefficient therefore depends on ice thickness and concen tration. It also depends on the floe size distribution, which is calculated by the WIM. The floe size distribution is defined by its probability density function p(d;x,t). The floe size distribution, and hence the attenuation coefficient, vary suddenly in time if wave-induced ice fracture occurs. The occurrence of fracture, in turn, depends on the wave energy spectrum. Calculation of the wave energy spectrum, S, and the floe size distribution, p, are therefore coupled via the attenuation coefficient.
量 cg 是波的群速度。Williams 等人（2013b）提供了数值证据，表明 WIM 预测的冰裂纹对波的色散不敏感。尽管这一发现并不具有决定性，但为了简化，当前应用中忽略了色散，即在输运方程中使用了一个常数值 cg。此外，假设波谱在时间框架内穿越了横截面的长度，即 cg = L/T, 从而减轻了指定 cg 值的需要。量 α(w;x,t) 是衰减系数，即每米波能量的指数衰减率。这里使用的表达式是 α = ca/{d)，其中 d 表示浮冰直径，⟨·⟩ 表示所包含量的平均值，a(ω, h) 是每块浮冰的衰减率，使用 Bennetts 和 Squire（2012）的模型计算。因此，衰减系数依赖于冰的厚度和浓度。它还依赖于浮冰大小分布，该分布由 WIM 计算。浮冰大小分布由其概率密度函数 p(d;x,t). 定义。如果发生波引起的冰裂纹，浮冰大小分布以及衰减系数会突然随时间变化。裂纹的发生又依赖于波能量谱。因此，波能量谱 S 和浮冰大小分布 p 通过衰减系数耦合在一起。

In order to isolate wave-ice interactions, the above version of the transport equation (1) neglects nonlinear transfer of wave energy between frequencies, wave energy input due to winds, long-range attenuation of swell, and attenuation due to wave breaking and whitecapping. To the authors' knowledge, the importance of these processes in the ice-covered ocean is not yet known. The fracture model derived by Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013a) is used. The model is based on strains imposed on the ice cover by wave motion, in which the ice is modelled as a thin-elastic beam. The fracture condition is
为了隔离波浪与冰的相互作用，上述传输方程 (1)的版本忽略了频率之间波能的非线性传递、风引起的波能输入、长距离涌浪的衰减以及由于波浪破裂和白浪造成的衰减。据作者所知，这些过程在冰覆盖的海洋中的重要性尚不清楚。使用了 Williams 等人（2013a）提出的断裂模型。该模型基于波动运动对冰盖施加的应变，其中冰被建模为一根薄弹性梁。断裂条件是

(2)

where E = 2 /m0[e] is the strain imposed on the ice by the waves. The quantity m 0 is the zeroth moment of strain. The nth moment of strain is defined as
其中 E = 2 /m0[e] 是波浪对冰施加的应变。量 m 0 是应变的零阶矩。应变的 n 阶矩定义为

(3)

where k is the ice-coupled wavenumber (Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others, 2013a). The quantity ∊ _c = σ_c/Y* is the fracture limit of the ice, where a_c is the flexural strength of the ice, Y* is the effective Young's modulus of the ice and Pc is a chosen critical probability.
其中 k 是冰耦合波数（Williams 等，2013a）。量 ∊ _c = σ_c/Y* 是冰的断裂极限，其中 a_c 是冰的弯曲强度，Y* 是冰的有效杨氏模量，Pc 是选择的临界概率。

The expressionMPa is used for the flexural strength, in which vb denotes brine volume fraction. Reference Timco and BrienTimco and O'Brien (1994) used 939 flexural strength measurements to derive the expression. (The root brine volume fraction ranged from 0.15 to 0.5, approximately, for those measurements obtained in situ using cantilever beams.)
表达式 MPa 用于弯曲强度，其中 vb 表示盐水体积分数。Timco 和 O'Brien (1994) 使用 939 个弯曲强度测量值推导出该表达式。（对于那些使用悬臂梁原位获得的测量值，根盐水体积分数大约在 0.15 到 0.5 之间。）

The expression Y* = {10(1 3.51 vb) 1 }GPa, as derived by Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013a), is used for the effective Young's modulus. (Williams and others noted that in situ measurements on large samples of sea ice often produce smaller values of the effective Young's modulus.)
表达式 Y* = {10(1 3.51 vb) 1 }GPa，由 Williams 等人（2013a）推导，用于有效的杨氏模量。（Williams 等人指出，对大块海冰的原位测量通常会产生较小的有效杨氏模量值。）

The critical probability limit for a narrow-band spectrum, Pc = exp (-1), is used. Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b) conducted a numerical study of the sensitivity of ice fracture to the value of the critical probability.
狭带谱的临界概率极限 Pc = exp (-1) 被使用。Williams 等人（2013b）进行了关于冰裂纹对临界概率值敏感性的数值研究。

Fracture occurs if inequality (2) is satisfied. If fracture occurs, the maximum floe diameter is set to be equal to half of the dominant wavelength, i.e. dmx = λ/2. The dominant wavelength is calculated from the dispersion relation for the ice-covered ocean (e.g. Bennetts and Squire, 2011), using the dominant wave period
如果满足不等式 (2)，则会发生断裂。如果发生断裂，最大浮冰直径被设定为主波长的一半，即 dmx = λ/2。主波长是根据冰盖海洋的色散关系计算的（例如，Bennetts 和 Squire，2011），使用主波周期。

(4)

is the nth spectral moment of the surface elevation 77 (WMO, 1998). The maximum floe diameter parameterizes the floe size distribution. The floe size distribution is otherwise specified. A truncated power-law floe size distribution is used. The corresponding probability density function is
是表面高度的第 n 阶谱矩 77 (WMO, 1998)。最大浮冰直径参数化浮冰大小分布。浮冰大小分布另有规定。使用截断幂律浮冰大小分布。相应的概率密度函数是

(5)

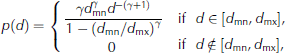
where dmn = 20 m is a chosen minimum floe diameter and 7 = 2 + log2(0.9) is the chosen exponent (Reference Dumont, Kohout and BertinoDumont and others, 2011; Reference Toyota, Haas and TamuraToyota and others, 2011; Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others, 2013a).
其中 dmn = 20 m 是选择的最小浮冰直径，7 = 2 + log2(0.9) 是选择的指数（Dumont 等，2011；Toyota 等，2011；Williams 等，2013a）。

Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b) used numerical results to show that W IM ice-fracture predictions are insensitive to the proportion of wave energy lost to ice fracture, if >30% of wave energy is lost to fracture. Experimental data do not exist to support or refute the assumption. It is therefore assumed that all wave energy is lost, i.e. steady-state conditions apply.
Williams 等人 (2013b) 使用数值结果表明，如果超过 30% 的波浪能量因冰裂而损失，则 W IM 冰裂预测对波浪能量损失到冰裂的比例不敏感。实验数据不存在以支持或反驳这一假设。因此假设所有波浪能量都被损失，即适用稳态条件。

Numerical Implementation  数值实现

New method without spatial or temporal discretizations
无空间或时间离散化的新方法

An ice cover acts as a low-pass filter to waves, i.e. the attenuation rate decreases as frequency decreases/period increases. Consequently, the wave spectrum increasingly skews towards low frequencies the farther it propagates into the ice-covered ocean, and the associated wavelength becomes larger. The maximum floe diameter thus increases with distance away from the ice edge in the wave-induced fracture region.
冰盖作为波浪的低通滤波器，即衰减率随着频率降低/周期增加而减少。因此，波谱在传播到冰盖覆盖的海洋中时，越来越偏向低频，相关的波长变得更大。因此，最大浮冰直径在波浪引起的断裂区域中随着远离冰缘的距离增加而增加。

The low-pass filter observation is the basis of an alternative numerical implementation of the WIM proposed below, which does not require spatial or temporal discretizations. The observation is translated to the assumption that the maximum floe diameter is due to ice fracture at the far end of the transect, x = L, or the farthest distance into the transect for which the wave spectrum is capable of causing fracture.
低通滤波器观测是下面提出的 WIM 替代数值实现的基础，该实现不需要空间或时间离散化。该观测被转化为假设，最大浮冰直径是由于在横断面远端的冰裂纹造成的，x = L, 或者是波谱能够导致裂纹的横断面最远距离。

The problem reduces to (1) determining if the wave spectrum at x = L is sufficient to cause ice fracture, and, if not, (2) determining the farthest point into the transect at which the wave spectrum is capable of causing ice fracture. However, the wave spectrum and the maximum floe diameter must be calculated simultaneously, because they are coupled via the attenuation coefficient.
问题归结为 (1) 确定在 x = L 处的波谱是否足以导致冰裂，如果不足以导致冰裂，(2) 确定波谱能够导致冰裂的横断面最远点。然而，波谱和最大浮冰直径必须同时计算，因为它们通过衰减系数相互耦合。

Suppose a trial value is specified for the maximum floe diameter, and hence the attenuation coefficient is known. The wave spectrum atx = L is then obtained directly from the energy-balance equation (1). The associated strain, EL(d_mx), and wavelength, λ _L (dmx), atx = L are calculated as described at the end of Section 2. Three scenarios are possible:
假设为最大浮冰直径指定了一个试验值，因此衰减系数是已知的。波谱在x = L时直接从能量平衡方程 (1)中获得。相关的应变EL(d_mx), 和波长λ _L (dmx)在x = L时按第 2 节末尾所述进行计算。可能有三种情况：

1. the maximum floe diameter is less than half the wavelength;
1. 最大浮冰直径小于波长的一半；

2. the maximum floe diameter is greater than half the wavelength; and
2. 最大浮冰直径大于半个波长；并且

3. the maximum floe diameter is equal to half the wavelength.
3. 最大浮冰直径等于波长的一半。

Scenario 3 is sought here. In scenario 3 the wavelength and the maximum floe diameter balance one another, i.e. the maximum diameter defines a floe size distribution that attenuates the wave spectrum such that the wavelength at x = L is consistent with the maximum diameter. The initial floe diameter is considered to be large. Note that the new method does not require a specific value to be prescribed for the initial maximum diameter.
这里寻求场景 3。在场景 3 中，波长和最大冰块直径相互平衡，即最大直径定义了一个冰块大小分布，该分布衰减波谱，使得在x = L时的波长与最大直径一致。初始冰块直径被认为是大的。请注意，新方法不需要为初始最大直径规定特定值。

The maximum diameter that balances the wavelength at x = L is obtained by finding the value of d _mx that satisfies the equation
在 x = L 时，平衡波长的最大直径是通过找到满足方程的 d_mx 的值来获得的

(6)

However, for this value of dmx, fracture only occurs if the strain imposed by the wave spectrum on the ice cover at x = L satisfies the inequality
然而，对于这个值的dmx，只有当波谱对x = L处冰盖施加的应变满足不等式时，才会发生断裂

(7)

Equation (6) can be solved numerically using a package root-finding algorithm (e.g. MATLAB ™'s fzero function). A check of fracture condition (7) is then performed for the calculated value of dmx.
方程 (6) 可以使用包根查找算法（例如 MATLAB ™ 的 fzero 函数）进行数值求解。然后对计算得出的 dmx 进行断裂条件 (7) 的检查。

Figure 1 shows results for a problem in which fracture occurs at x = L = 100 km. A Bretschneider incident wave spectrum is used. It is defined by a peak period and a significant wave height, which is convenient for model testing. For this problem, the incident peak period is 9.5 s and the significant wave height is 1 m. However, any incident wave spectrum can be used, including ones derived from observations or wave models such as WAM or Wavewatch.
图 1 显示了一个在 x = L = 100 公里处发生断裂的问题的结果。使用了 Bretschneider 入射波谱。它由一个峰值周期和一个显著波高定义，这对于模型测试很方便。对于这个问题，入射峰值周期为 9.5 秒，显著波高为 1 米。然而，可以使用任何入射波谱，包括从观测或波模型（如 WAM 或 Wavewatch）得出的波谱。

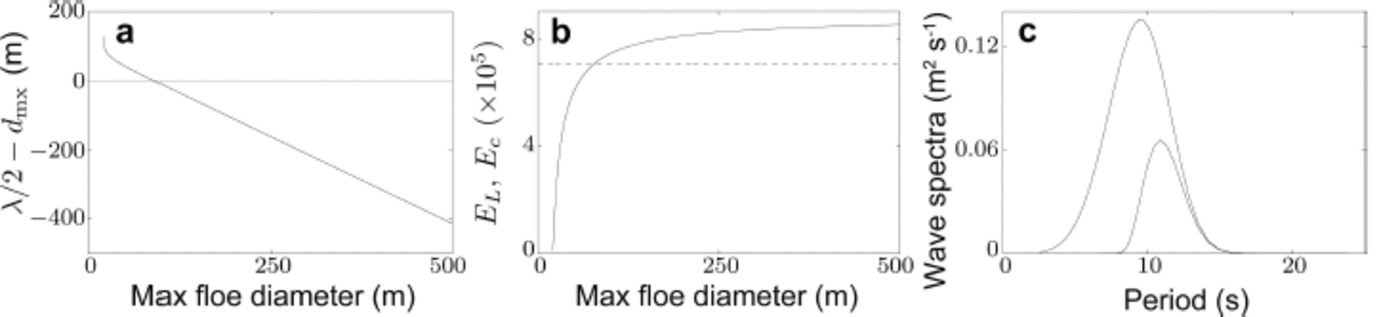
Fig. 1. Results for incident wave spectrum with 1 m significant wave height and 9.5 s peak period, and transect length L = 100 km. (a) Black curve represents half-wavelength/maximum-floe-diameter balance function at x = L. Grey curve represents abscissa axis. (b) Solid curve represents strain imposed on the ice by wave spectrum at x = L, as a function of maximum floe diameter. Broken curve represents the strain threshold E_c . (c) Incident wave spectrum and attenuated wave spectrum at x = L.
图 1. 具有 1 米显著波高和 9.5 秒峰值周期的入射波谱结果，横断面长度 L = 100 公里。 (a) 黑色曲线表示在 x = L 时的半波长/最大浮冰直径平衡函数。灰色曲线表示横坐标轴。 (b) 实线曲线表示在 x = L 时波谱对冰施加的应变，作为最大浮冰直径的函数。虚线曲线表示应变阈值 E_c 。 (c) 在 x = L 时的入射波谱和衰减波谱。

Figure 1a shows the difference between the half-wavelength at x = L and the maximum floe diameter, for a given maximum floe diameter. The half-wavelength and maximum floe diameter balance one another at ∼89.5 m. Figure 1b shows the corresponding strain imposed by the wave spectrum on the ice cover, as a function of maximum floe diameter, and the strain threshold, E_c. It confirms that the wave spectrum is sufficiently intense to fracture the ice cover when dmx ≈ 89.5 m.
图 1a 显示了在给定最大浮冰直径下，x = L 处的半波长与最大浮冰直径之间的差异。半波长和最大浮冰直径在 ∼89.5 m 时相互平衡。图 1b 显示了波谱对冰盖施加的相应应变，作为最大浮冰直径的函数，以及应变阈值 E_c. 它确认当 dmx ≈ 89.5 m 时，波谱的强度足以使冰盖破裂。

The maximum floe diameter is therefore set as dmx ≈ 89.5 m. Figure shows the incident wave spectrum and the attenuated wave spectrum at x = L Skew of the attenuated spectrum towards long periods is clear.
因此，最大浮冰直径设定为 dmx ≈ 89.5 m。图中显示了在 x = L 处的入射波谱和衰减波谱，衰减波谱向长周期的偏斜非常明显。

If the fracture condition is not satisfied at x = L, the problem is extended to search for the greatest distance into the transect at which the wave spectrum is capable of causing fracture. The extension is necessary, as wave-induced fracture may be possible for a large proportion of the transect, despite not being possible for the entire transect.
如果在x = L,处不满足断裂条件，则问题扩展为寻找波谱能够导致断裂的剖面中最大的距离。这个扩展是必要的，因为尽管在整个剖面中可能无法发生波引起的断裂，但在剖面的很大一部分中可能是可行的。

Let x = l be the greatest distance at which fracture can occur. The strain imposed on the ice cover by the wave spectrum at this point, E_l (d _mx), is such that
让x = l成为可能发生断裂的最大距离。在这一点上，波谱对冰盖施加的应变 E(d_mx)是这样的：

(8a)

Additionally, the wavelength at x = l, λ _l , must balance the maximum diameter, i.e.
此外，x = l, 的波长 λ 必须平衡最大直径，即

(8b)

Equations (8a) and (8b) are to be solved simultaneously for l and d _mx. In practice, the equations are solved numerically as a set of one-dimensional equations:1. by solving Eqn (8b) to give the maximum diameter that balances the wave spectrum, as a function of distance l,
方程 (8a) 和 (8b) 需要同时求解 l 和 d_mx。在实际中，这些方程作为一组一维方程进行数值求解：1. 通过求解方程 (8b) 来给出平衡波谱的最大直径，作为距离 l 的函数，

i.e. d _mx = d_mx(l); and
即 d_mx = d_mx(l); 并且

2. substituting the expression for d _mx = d_mx(l) into Eqn (8a) and solving for the distance l.
2. 将d_mx = d_mx(l)的表达式代入方程(8a)并求解距离l。

The extended method is necessary for a problem identical to that used above (Fig. 1) but with a 0.8 m significant wave height for the incident spectrum. Figure 2 shows results produced by the extended method. As in Figure 1, the left-hand and middle panels show the balance equation and strains at x = L. The half-wavelength and maximum floe diameter again balance one another at ∼89.5 m. However, the wave spectrum at x=L= 100 km is not sufficiently intense to fracture the ice for d _mx ≈ 89.5 m (or for any dmx less than 500 m; Fig. 2b). Figure 2c shows the strain balance equation as a function of distance l. The largest distance at which the wave spectrum remains sufficiently intense to fracture the ice is ∼71.3km, i.e. wave-induced fracture occurs over a substantial proportion of the transect.
扩展方法对于一个与上述相同的问题是必要的（图 1），但入射谱的显著波高为 0.8 米。图 2显示了扩展方法产生的结果。与图 1一样，左侧和中间面板显示了平衡方程和在x = L.处的应变。半波长和最大浮冰直径再次在约 89.5 米处相互平衡。然而，在x=L= 100 公里处的波谱强度不足以使冰块破裂，对于d_mx ≈ 89.5 米（或任何小于 500 米的dmx；图 2b）。图 2c显示了应变平衡方程作为距离l的函数。波谱保持足够强度以使冰块破裂的最大距离约为 71.3 公里，即波引起的破裂发生在横断面的大部分区域。

Fig. 2. (a, b) Same as Figure 1 but for 0.8 m incident significant wave height. (c) Corresponding strain balance equation as a function of distance, l. In (b) and (c) grey curves represent abscissa axes.
图 2. (a, b) 与 图 1 相同，但对于 0.8 米的入射显著波高。 (c) 相应的应变平衡方程作为距离的函数。在 (b) 和 (c) 中，灰色曲线表示横坐标轴。

The two numerical implementations use different interpretations of the floe size distribution. The new method uses a single maximum floe diameter for the transect, which, recall, represents a single cell in an OGCM. The floe size distribution, p, for the entire transect is parameterized by the maximum floe diameter. In contrast, the method of Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b) considers the floe size distribution to be a property of the subcells of the transect, i.e. a maximum floe diameter is assigned to each subcell. The floe size distribution for the entire transect is generally not of the form p.
这两种数值实现对浮冰大小分布的解释不同。新方法对横断面使用单一的最大浮冰直径，回想一下，这代表了 OGCM 中的一个单元格。整个横断面的浮冰大小分布，p，由最大浮冰直径参数化。相比之下，Williams 等人（2013b）的方法认为浮冰大小分布是横断面子单元的一个属性，即每个子单元分配一个最大浮冰直径。整个横断面的浮冰大小分布通常不是p的形式。

Figure 3 compares results produced by the two methods, for an example problem. Figure 3a shows fracture width, defined as the distance of the transect over which wave-induced fracture occurs, as a function of the peak period of the incident wave spectrum. Figure 3b shows maximum floe diameter in the fractured region, as a function of peak period. The length of the transect is set to be very large so that the fractured region is not truncated. The significant wave height of the incident spectrum is 1 m.
图 3 比较了两种方法在一个示例问题中产生的结果。图 3a 显示了裂缝宽度，定义为波引起裂缝发生的横截面的距离，作为入射波谱的峰值周期的函数。图 3b 显示了裂缝区域的最大浮冰直径，作为峰值周期的函数。横截面的长度设置得非常大，以便裂缝区域不被截断。入射波谱的显著波高为 1 米。

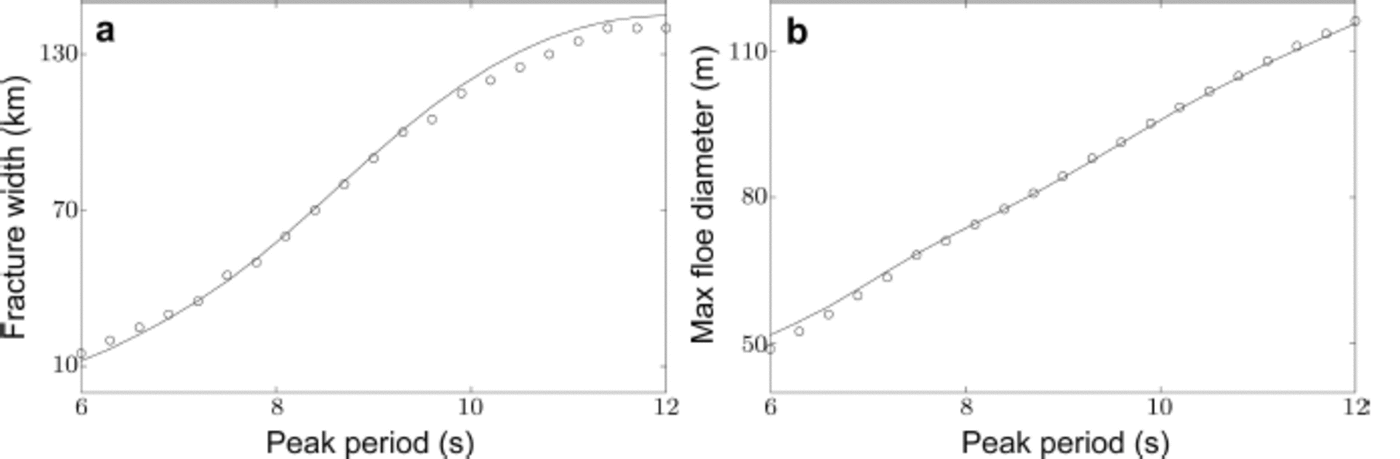
Fig. 3. Fracture width (a) and maximum floe diameter (b), as functions of incident wave spectrum peak period. Incident wave spectrum significant wave height is 1 m. Circles and curves denote results produced by method of Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b) and new method, respectively.
图 3. 断裂宽度 (a) 和最大浮冰直径 (b) 作为入射波谱峰值周期的函数。入射波谱显著波高为 1 米。圆圈和曲线分别表示 Williams 等人 (2013b) 的方法和新方法产生的结果。

Fracture width and maximum floe diameter both increase as peak period increases. The increase in fracture width becomes less rapid as peak period increases. The relationship between maximum floe diameter and peak period is approximately linear for the interval considered.
随着峰值周期的增加，裂缝宽度和最大浮冰直径都在增加。随着峰值周期的增加，裂缝宽度的增加变得不那么迅速。对于考虑的区间，最大浮冰直径与峰值周期之间的关系大致是线性的。

Given the different interpretations of the floe size distribution in the two methods, the agreement in the results is reassuring. (Slight differences for the predicted fracture widths can be attributed, in part, to discontinuities resulting from discretization of the transect in the method of Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b) - a 5 km cell length was used for the example.) The results therefore indicate the WIM is insensitive to precise knowledge of the floe size distribution.
考虑到两种方法对冰块大小分布的不同解释，结果的一致性令人放心。（预测的断裂宽度的轻微差异部分可以归因于威廉姆斯等人（2013b）方法中横断面的离散化所导致的不连续性 - 示例中使用了 5 公里的单元长度。）因此，结果表明 WIM 对冰块大小分布的精确知识不敏感。

Summary and Discussion  总结与讨论

A new numerical implementation has been applied to a modified version of the WIM proposed by Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b). The new method was based on the assumption that the maximum floe diameter occurs at the far end of the cell. At the far boundary the dominant wavelength is at its maximum, as the wave attenuation due to ice cover skews the wave spectrum towards long period waves.
一种新的数值实现已应用于 Williams 等人（2013b）提出的 WIM 的修改版本。新方法基于假设最大浮冰直径发生在单元的远端。在远边界，主导波长达到最大，因为冰盖导致的波衰减使波谱偏向长周期波。

The maximum floe diameter was used to define the floe size distribution in the cell. A wavelength/maximum-floe-size equation was posed on the far boundary and solved to obtain the wave attenuation rate and floe size distribution, simultaneously. If the wave spectrum was not sufficiently intense to fracture the ice at the far boundary, the problem was extended to search for the farthest distance into the cell at which fracture occurs.
最大浮冰直径用于定义单元中的浮冰大小分布。在远边界提出了一个波长/最大浮冰大小方程，并同时求解以获得波衰减率和浮冰大小分布。如果波谱的强度不足以在远边界处破裂冰层，则问题被扩展以寻找在单元中发生破裂的最远距离。

The new method was presented for an idealized transect geometry. Example results for the width of the fractured ice region, and maximum floe diameter due to wave-induced fracture, as functions of peak wave period were given. The results were compared to results produced by the method of Reference Williams, Bennetts, Squire, Dumont and BertinoWilliams and others (2013b). The two methods gave almost identical results. Close agreement was not guaranteed, as the methods adopt different interpretations of the floe size distribution.
该新方法是针对理想化的横断面几何形状提出的。给出了波浪引起的断裂导致的裂冰区域宽度和最大浮冰直径的示例结果，作为峰值波周期的函数。结果与 Williams 等人（2013b）的方法产生的结果进行了比较。这两种方法给出的结果几乎相同。由于这两种方法对浮冰大小分布的解释不同，因此并不能保证结果的高度一致。

Integration of the WIM into OGCMs will require, in the first instance, an extension to two-dimensional (2-D) geometries. The key assumption of the new method, which is that the maximum floe diameter occurs at the far end of a cell, can be reinterpreted directly in the 2-D setting. However, the validity of the key assumption must be tested for directional wave spectra and multiple thickness categories.
将 WIM 集成到 OGCM 中，首先需要扩展到二维（2-D）几何形状。新方法的关键假设是最大浮冰直径发生在单元的远端，这可以直接在二维环境中重新解释。然而，必须对方向波谱和多个厚度类别测试关键假设的有效性。