1 Introduction 1 簡介

The last decade has witnessed considerable progress in the development of multiscale entropy method [1], especially for the analysis of physiological time series in revealing underlying complex dynamics of the system. The concept of entropy has been widely used to measure complexity of a system. The idea was initially developed from the classic Shannon entropy [2]. In mathematics, the Shannon entropy of a discrete random variable X is defined as: H(X)=−∑xP(x)log2[P(x)], where P(x) is the probability that X is in the event x, and P(x)log 2[P(x)] is defined as 0 if P(x) = 0. From the equation, if one of the events occurs more frequent than others, observation of that event bears less informative. Conversely, less frequent events provide more information when observed. Entropy is calculated as zero when the outcome is certain. Thus, given a known probability distribution of the source, Shannon entropy quantifies all these considerations exactly, providing a way to estimate the average minimum number of bits needed to encode a string of symbols, based on the frequency of the symbols, which also provides a basis for the ensuing development within the framework of information theory. Among many entropy measures developed such as Kolmogorov–Smirnov (K–S) entropy [3], E–R entropy [4] and compression entropy [58], approximate entropy (ApEn) [5] has been highlighted as one of most effective methods to provide a relatively robust measure of entropy, particularly for short and noisy time series. Sample Entropy [6], as a further development, was used to correct the bias of the ApEn algorithm. All these entropy methods did not consider the multiscale nature of the underlying signals, thus could yield misleading results for complex multiscale system [1]. In reality the signals derived from physiological and complex systems usually have multiple spatiotemporal scales. Therefore, the multiscale entropy [1] was proposed as a new measure of complexity in order to scrutinize complex time series by taking into account different scales. Since its first application to analysis of human heartbeat time series signal [1, 7], the multiscale entropy has been increasingly applied to analyze not only cardiovascular signal [8,9,10], but also many different physiological time series signals for various applications. For instance, the multiscale entropy has been employed to perform the analysis of (1) electroencephalogram [11, 12], functional magnetic resonance imaging [13] and magnetoencephalogram [14] signals to investigate the nonlinear dynamics in brain; (2 the gait time series to explore the gait dynamic [15]; (3) the laser speckle contrast images to examine the aging effect on microcirculation [16]; (4) the lung sound signal to classify the different lung status [17] and (5) the alternative medicine study [18]. In addition to the physiological signal, the multiscale entropy recently has also been utilized to the mechanic fault detection [19,20,21], the characterization of the physical structure of complex system [22,23,24], nonlinear dynamic analysis of financial market [25,26,27,28,29], complexity examination of traffic system [30, 31] and the nonlinear analysis in geophysics [32,33,34].
過去十年來，在多尺度熵方法的發展方面取得了相當大的進展，特別是在分析生理時間序列以揭示系統潛在複雜動態方面。熵的概念被廣泛應用於衡量系統的複雜性。這個想法最初是從經典的 Shannon 熵中發展而來。在數學中，離散隨機變量 X 的 Shannon 熵被定義為：，其中 P(x)是 X 在事件 x 中的概率，而 P(x)log [P(x)]在 P(x) = 0 時被定義為 0。根據這個方程，如果某個事件比其他事件更頻繁地發生，觀察到該事件時所帶來的信息較少。相反，較不頻繁的事件在觀察時提供更多信息。當結果確定時，熵被計算為零。因此，鑒於源頭的已知概率分佈，Shannon 熵確切地量化了所有這些考慮，提供了一種根據符號的頻率來估計編碼一串符號所需的平均最小位數的方法，這也為信息理論框架內的後續發展提供了基礎。 在許多熵測量方法中，如科爾莫哥洛夫-斯米爾諾夫（K-S）熵[3]、E-R 熵[4]和壓縮熵[58]等，近似熵（ApEn）[5]被認為是提供相對穩健的熵測量方法之一，特別適用於短且嘈雜的時間序列。作為進一步發展，樣本熵[6]被用來校正 ApEn 算法的偏差。所有這些熵方法都沒有考慮底層信號的多尺度性質，因此對於複雜的多尺度系統可能產生誤導性結果。實際上，從生理和複雜系統中得出的信號通常具有多個時空尺度。因此，多尺度熵[1]被提出作為一種新的複雜度測量方法，以考慮不同尺度來檢視複雜時間序列。自從首次應用於人類心跳時間序列信號的分析[1, 7]以來，多尺度熵已越來越廣泛地應用於分析不僅心血管信號[8, 9, 10]，還有許多不同生理時間序列信號的各種應用。 例如，多尺度熵已被用於分析腦電圖[11,12]、功能性磁共振成像[13]和腦磁圖[14]信號，以研究大腦中的非線性動態；(2) 步態時間序列以探索步態動態[15]；(3) 激光散斑對比影像以檢驗微循環的老化效應[16]；(4) 肺音信號以區分不同的肺部狀態[17]和(5) 替代醫學研究[18]。除了生理信號外，多尺度熵最近還被用於機械故障檢測[19,20,21]、複雜系統的物理結構特徵化[22,23,24]、金融市場的非線性動態分析[25,26,27,28,29]、交通系統的複雜性檢驗[30,31]和地球物理學中的非線性分析[32,33,34]。

In terms of methodological development, the multiscale entropy can be implemented in two steps: (1) extraction of different scales of time series, and (2) calculation of entropy over those extracted scales. In the original development of the multiscale entropy [1], the scales of data are determined by the so-called coarse-grained procedure, whereby the raw time series at individual scale is first divided into the nonoverlapping windows, and each window is then replaced by its average [3], upon which the sample entropy is applied. For instance, to generate the consecutive coarse-grained time series at the scale factor Ґ, the original time series was first divided into nonoverlapping windows of length Ґ and the data points within each window were averaged. For scale one (i.e., Ґ = 1), the coarse-grained time series is simply the original time series. The length of each coarse-grained time series is equal to the length of the original time series divided by the scale factor. This ‘coarse-graining’ procedure essentially represents a linear smoothing and decimation to progressively eliminate the fast temporal component from the original signal, which nonetheless might be suboptimal due to the way the scale is extracted [35]. On the other hand, the sample entropy has been criticized for the inaccurate estimation or too sensitive to the choices of the parameters [36]. For example, in sample entropy, the Heaviside function is employed to assess the similarity between the embedded data vectors, which is like a two-state classifier: the contributions of all the data points inside the boundary are treated equally, while the data points outside the boundary are abandoned. As a result, sample entropy may vary dramatically when the tolerance parameter r is slightly changed. As such, different methods have been developed to improve the multiscale entropy estimation. In this chapter, we aim to provide a systematic review for these algorithms and offer some insight for future directions. In what follows, we specifically focus on two aspects of development: (1) extraction of the scales, and (2) estimation of the entropy. From each step of development of the multiscale entropy method, it has also been seen that the multiscale entropy method has been being utilized in the much expanded areas. Specifically, we provide a short overview on the application of multiscale entropy to the analysis of cardiovascular time series. We finally conclude the chapter with discussions.
在方法論發展方面，多尺度熵可以通過兩個步驟實現：（1）提取不同尺度的時間序列，以及（2）在這些提取的尺度上計算熵。在多尺度熵的原始發展中，數據的尺度是通過所謂的粗粒化程序確定的，即首先將單個尺度的原始時間序列劃分為非重疊窗口，然後將每個窗口替換為其平均值，然後應用樣本熵。例如，為了生成尺度因子Ґ的連續粗粒化時間序列，原始時間序列首先被劃分為長度為Ґ的非重疊窗口，然後每個窗口內的數據點被平均。對於尺度為一（即Ґ = 1），粗粒化時間序列就是原始時間序列。每個粗粒化時間序列的長度等於原始時間序列的長度除以尺度因子。 這個「粗粒化」程序基本上代表了對原始信號進行線性平滑和抽取，逐步消除快速時間成分，儘管這可能因為尺度提取方式而不夠理想。另一方面，樣本熵被批評為估計不準確或對參數選擇過於敏感。例如，在樣本熵中，海維塞德函數被用來評估嵌入數據向量之間的相似性，這就像一個雙狀態分類器：邊界內所有數據點的貢獻被平等對待，而邊界外的數據點被放棄。因此，當容忍參數 r 稍微改變時，樣本熵可能會劇烈變化。因此，已經開發了不同的方法來改進多尺度熵的估計。在本章中，我們旨在對這些算法進行系統性回顧，並為未來方向提供一些見解。接下來，我們專注於兩個發展方面：(1) 尺度的提取，和 (2) 熵的估計。 從多尺度熵方法的每一個發展步驟中，也可以看到多尺度熵方法被廣泛應用在許多領域。具體來說，我們提供了多尺度熵應用於心血管時間序列分析的簡要概述。最後，我們以討論結束本章。

2 Overview of Multiscale Entropy
多尺度熵概述

The multiscale entropy [1] was developed to measure the complexity/irregularity over the different scales of time series. The scales are determined by the ‘coarse-grained’ procedure, where the length of the coarse-grained time series is equal to the length of original time series divided by the scale factor. At each time scale, sample entropy is used to determine the amount of irregularity to provide the entropy estimation. The sample entropy is thought of as a robust measure of entropy at a single scale due to its insensitivity to the data length and immunity to the noise in the data [6]. It is equal to the negative natural logarithm of the conditional probability that m consecutive points that repeat themselves, within some tolerance, r, will again repeat with the addition of the next (m + 1) point.
多尺度熵[1]是為了測量時間序列在不同時間尺度上的複雜性/不規則性而開發的。這些尺度是通過“粗粒化”程序確定的，其中粗粒化時間序列的長度等於原始時間序列的長度除以尺度因子。在每個時間尺度上，使用樣本熵來確定不規則性的量以提供熵估計。樣本熵被認為是在單個尺度上的熵的一個穩健度量，因為它對數據長度不敏感且對數據中的噪音具有免疫性[6]。它等於 m 個連續重複的點在某個容忍度 r 內再次重複並加上下一個（m + 1）點的條件概率的負自然對數。

To compute sample entropy, a time series I = {i(1), i(2),  … , i(N)} is first embedded in a m-dimensional space, in which the m-dimensional vectors of the time series are constructed as x m (k) = (i(k), i(k + 1),  … , i(k + m − 1)) , k = 1 ∼ N − m + 1. In the embedded space, the match of any two vectors is defined as their distance lower than the tolerance r. The distance between two vectors refers to as the maximum difference between their corresponding scalar components. B m(r) is defined as the probability that two vectors match within a tolerance r in the m-dimensional space, where self-matches are excluded. Similarly, A m(r) is defined in the m + 1 dimensional space. Sample entropy is then defined as the negative natural logarithm of the conditional probability that two sequences similar for m points remain similar at the next m + 1 point in the data set within a tolerance r, which is calculated as:
為了計算樣本熵，首先將時間序列 I = {i(1), i(2), … , i(N)} 嵌入到一個 m 維空間中，其中時間序列的 m 維向量被構造為 x m (k) = (i(k), i(k + 1), … , i(k + m − 1))，k = 1 ∼ N − m + 1。在嵌入空間中，任意兩個向量的匹配被定義為它們的距離低於容忍度 r。兩個向量之間的距離指的是它們對應標量分量之間的最大差異。B m (r) 被定義為在 m 維空間中兩個向量在容忍度 r 內匹配的概率，其中排除了自我匹配。同樣地，A m (r) 在 m + 1 維空間中被定義。然後，樣本熵被定義為兩個相似序列在 m 點保持相似並在下一個 m + 1 點中在容忍度 r 內的條件概率的負自然對數，計算公式如下：

SampEn(I,m,r)=−ln⁡(Am(r)Bm(r))

As a result, regular and/or periodic signals have theoretical sample entropy of 0, whereas uncorrelated random signals have maximum entropy depending on the signal length.
因此，規則和/或周期信號的理論樣本熵為 0，而不相關的隨機信號具有取決於信號長度的最大熵。

The multiscale entropy can then be obtained by applying the sample entropy across multiple time scales. This is achieved through a coarse-graining procedure, whereby, i.e., at the scale n, the raw time series first is divided into the nonoverlaping windows with the length of n, and each window is then replaced by its average. For instance, at the first scale, the multiscale entropy algorithm evaluates sample entropy for the original time-series. For the second scale (i.e., n = 2), the original time-series (length L) is first divided into non-overlapping windows of length 2. Within each window the average is taken, resulting in a new time-series of length L/2, over which the sample entropy is computed. The procedure is repeated until the last time scale is accomplished. Therefore the coarse-grained procedure essentially represents a linear smoothing and decimation (down sampling) of the original time series. Despite the wide applications, the multiscale entropy approach however has several limitations:
多尺度熵可以通過在多個時間尺度上應用樣本熵來獲得。這是通過一個粗粒化過程實現的，即，在尺度 n 上，原始時間序列首先被劃分為長度為 n 的非重疊窗口，然後每個窗口被其平均值替換。例如，在第一個尺度上，多尺度熵算法評估原始時間序列的樣本熵。對於第二個尺度（即 n = 2），原始時間序列（長度 L）首先被劃分為長度為 2 的非重疊窗口。在每個窗口內取平均值，得到一個新的長度為 L/2 的時間序列，計算其樣本熵。該過程重複進行，直到完成最後一個時間尺度。因此，粗粒化過程基本上代表了原始時間序列的線性平滑和抽取（下採樣）。儘管多尺度熵方法有廣泛的應用，但也存在一些限制：

  1. 1.

    The coarse-graining procedure has the effect of down sampling on original time series, which reduces the original sampling rate of a time series to a lower rate, losing the high-frequency component of the signal. Thus, the multiscale entropy only captures the low-frequency components and thus does not entail the high-frequency components as the scales were extracted. Yet there is little reason to ignore the high-frequency components in signal, which may retain significant information in the system [35, 37].
    粗粒化程序對原始時間序列進行了下採樣，將時間序列的原始採樣率降低到較低的速率，從而失去了信號的高頻成分。因此，多尺度熵僅捕捉低頻成分，因此不包含高頻成分，因為所提取的尺度。然而，在信號中忽略高頻成分並無太多理由，這些成分可能保留了系統中的重要信息。

  2. 2.

    Due to the linear operations, the algorithm for extracting the different scales is not well adapted to nonlinear/nonstationary signals, particularly in physiological system. Considering the coarse-grained process as a filter, the features of its frequency response are poor since it shows side lobes in the stopband [35, 38].
    由於線性操作，用於提取不同尺度的算法對非線性/非穩態信號不適應，特別是在生理系統中。將粗粒化過程視為濾波器，其頻率響應的特性很差，因為在阻帶中顯示出側瓣[ 35, 38]。

  3. 3.

    With ‘Coarse-graining’, the larger the scale factor, the shorter the coarse-grained time series. As the scale increases, the number of data points is reduced [39, 40]. The variance of the estimated entropy gets quickly increased; hence the statistical reliability of entropy measure is greatly diminished.
    通過“粗粒化”，尺度因子越大，粗粒化時間序列越短。隨著尺度的增加，數據點的數量減少[ 39, 40]。估計熵的變異性迅速增加；因此，熵測量的統計可靠性大大降低。

As a result, several methods have been proposed to overcome these shortcomings. We will review those improvements by focusing on the extraction of the scales and the enhancements of entropy estimation. Table 4.1 below briefly summarizes the key information for these methods.
因此，已提出幾種方法來克服這些缺點。我們將通過專注於尺度的提取和熵估計的增強來回顧這些改進。下面的表 4.1 簡要概述了這些方法的關鍵信息。

Table 4.1 Summary of developed multiscale entropy methods
表 4.1 開發的多尺度熵方法摘要
Full size table 完整尺寸表

3 Methods for Scale Extraction
3 種尺度提取方法

3.1 Composite Multiscale Entropy
3.1 複合多尺度熵

The composite multiscale entropy [39] was developed to address the statistical reliability issue of the multiscale entropy. As described above, in original development of multiscale entropy, the length of coarse-grained time series is shorter when the scale factor becomes larger, leading to the larger variance of sample entropy estimation at greater scales. Thus large variance of estimated entropy values results in the reduction of reliability of multiscale entropy estimation.
複合多尺度熵[39]是為了解決多尺度熵的統計可靠性問題而開發的。如上所述，在多尺度熵的原始開發中，當尺度因子變大時，粗粒化時間序列的長度變短，導致在較大尺度上對樣本熵估計的變異性增加。因此，估計熵值的大變異導致多尺度熵估計的可靠性降低。

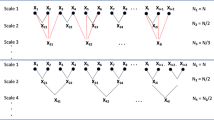
To address this issue, the composite multiscale entropy was developed to first generate multiple unique coarse-grained time series at a certain scale factor (e.g., 3) by changing the starting point (e.g., 1st, 2nd, 3rd) of time series in the coarse-graining procedure, and then calculate sample entropy on each coarse-grained time series, and finally take average of all the calculated sample entropy values. Such a modified coarse-graining procedure is illustrated in Fig. 4.1.
為了解決這個問題，開發了複合多尺度熵，首先通過改變粗粒化程序中時間序列的起始點（例如，第 1、2、3 個）在某個尺度因子（例如 3）生成多個獨特的粗粒化時間序列，然後在每個粗粒化時間序列上計算樣本熵，最後將所有計算出的樣本熵值取平均。這種修改後的粗粒化程序在圖 4.1 中有所說明。

Fig. 4.1 圖 4.1
figure 1

The modified coarse-graining procedure used by composite multiscale entropy
复合多尺度熵使用的修改后的粗粒化程序

Full size image 全尺寸圖像

As shown in [39], both the simulated (e.g., white noise and 1/f noise) and real vibration data (e.g., Figs. 8 and 10 in [39]) show that the composite multiscale entropy yielded the almost same mean estimation with the multiscale entropy, but with much more accurate individual estimation, which is manifested as the smaller standard deviation values of entropy estimation on scales by the composite multiscale entropy than those by the multiscale entropy.
如[ 39]所示，模擬（例如，白噪聲和 1/f 噪聲）和真實振動數據（例如[ 39]中的圖 8 和圖 10）顯示，複合多尺度熵與多尺度熵具有幾乎相同的平均估計，但在個別估計方面更準確，這表現為複合多尺度熵在尺度上的熵估計的標準偏差值比多尺度熵小。

Subsequently, the composite multiscale entropy [40] was refined to further improve the performance in terms of entropy estimation, as it was observed that in composite multiscale entropy, though the multiple coarse-grained time series at individual scales facilitate the accurate estimation of entropy, the method also increases the probability of inducing undefined entropy. Instead of calculating average of sample entropy values over all the coarse-grained time series at single scale, the refined composite multiscale entropy first collected the number of matched patterns over all the coarse-grained time series for the selected parameter m (i.e., collecting the numbers of the matched patterns for both m and m + 1, according to the sample entropy algorithm), and then applied the sample entropy algorithm to calculate the negative natural logarithm of the conditional probability, hence reducing the probability of undefined entropy values. In the Reference [40], the simulated data (white noise and 1/f noise) showed that the refined composite multiscale entropy is superior to both the multiscale entropy and composite multiscale entropy by increasing the accuracy of entropy estimation and reducing the probability of inducing undefined entropy, particularly for short time series data. This can be clearly seen from the Table 2 in [40] that the refined composite multiscale entropy can still work on the shorter time series data and provide the smaller standard deviation of entropy estimations on scales than multiscale entropy and composite multiscale entropy. Furthermore, the refined composite multiscale entropy can be further improved by incorporating with empirical mode decomposition (EMD) algorithm for the purpose of removing the data baseline before calculating the entropy [41].
隨後，複合多尺度熵[40]被改進以進一步提高熵估計的性能，因為觀察到在複合多尺度熵中，雖然在各個尺度上的多個粗粒化時間序列有助於準確估計熵，但該方法也增加了誘發未定義熵的概率。改進後的複合多尺度熵不是計算單一尺度上所有粗粒化時間序列的樣本熵值的平均值，而是首先收集選定參數 m（即根據樣本熵算法收集 m 和 m + 1 的匹配模式數），然後應用樣本熵算法計算條件概率的負自然對數，從而降低未定義熵值的概率。 在參考文獻[40]中，模擬數據（白噪聲和 1/f 噪聲）顯示，通過提高熵估計的準確性並減少誘發未定義熵的概率，精煉的複合多尺度熵優於多尺度熵和複合多尺度熵，特別是對於短時間序列數據。從[40]中的表 2 可以清楚地看出，精煉的複合多尺度熵仍然可以應用於較短的時間序列數據，並且在各尺度上提供比多尺度熵和複合多尺度熵更小的熵估計標準差。此外，通過將經驗模態分解（EMD）算法與精煉的複合多尺度熵結合，可以進一步改進，以在計算熵之前去除數據基線[41]。

It should be mentioned that by the same idea of composite multiscale entropy in generating multiple coarse-grained time series, the so-called short-time multiscale entropy [42] was independently developed to address the issue of multiscale entropy when facing with short time series data.
應該提到，通過在生成多個粗粒度時間序列時使用複合多尺度熵的相同思想，所謂的短時間多尺度熵[42]是獨立開發的，以應對處理短時間序列數據時的多尺度熵問題。

3.2 Modified Multiscale Entropy for Short Time Series
3.2 短時間序列的修改多尺度熵

As indicated by its name, the modified multiscale entropy was proposed to address the reliability of multiscale entropy when time series is short [43]. With the same rationale as the above-mentioned composite multiscale entropy, this method tended to offer the better accuracy of entropy estimation or fewer undefined entropy when the time series is short. In essence, the modified multiscale entropy replaced the coarse-graining procedure with a moving-average process, in which a moving window with length of scale factor was slid through the whole time series point-by-point to generate the new time series at the scale. By doing so, data length was largely reserved, compared to the coarse-graining procedure. For instance, at the scale of 2, a time series with 1000 data points is changed into a new time series with 500 data points by the coarse graining procedure, while by the moving-average procedure, the new time series becomes 999 data points.
根據其名稱，修改後的多尺度熵是為了解決當時間序列較短時多尺度熵的可靠性而提出的。與上述的複合多尺度熵相同的原理，這種方法傾向於在時間序列較短時提供更準確的熵估計或更少未定義的熵。實質上，修改後的多尺度熵將粗粒化程序替換為移動平均過程，其中一個長度為尺度因子的移動窗口逐點滑過整個時間序列，以生成在該尺度下的新時間序列。通過這樣做，與粗粒化程序相比，數據長度得到了很大程度的保留。例如，在尺度為 2 時，一個包含 1000 個數據點的時間序列通過粗粒化程序變為包含 500 個數據點的新時間序列，而通過移動平均程序，新時間序列變為 999 個數據點。

In [43], both simulation (white noise and 1/f noise) and real vibration data were performed to validate the effectiveness of proposed method for short time series data. For both white noise and 1/f noise with 1 k data points, the modified multiscale entropy provides the sample entropy curve with the less fluctuation than the conventional sample entropy in a typical example. By using 200 independent noise samples for both white noise and 1/f noise, each noise sample contained 500 data points, the results show that the modified multiscale entropy offers the nearly equal mean of entropy estimations with the sample entropy over independent samples, but with the less the standard deviation of entropy estimations than the sample entropy, indicating that the modified multiscale entropy and multiscale entropy methods are nearly equivalent statistically; however, the former method can provide a more accurate estimate than the conventional multiscale entropy. The applications of methods to the real bearing vibration data also show the consistent conclusions. However, it should be mentioned that considering the computational cost and the limited improvement for longer time series, the modified multiscale entropy is not suitable for direct application in analyzing longer time series. For instance, from the Table 2 in [43], it is seen that for the 1/f noise with data length of 30 k, the modified multiscale entropy provides the almost same entropy estimations (including mean and standard deviation over independent samples) with the sample entropy, but demanding significantly heavier computational cost.
在[43]中，進行了模擬（白噪聲和 1/f 噪聲）和真實振動數據，以驗證所提出的短時間序列數據方法的有效性。對於具有 1k 數據點的白噪聲和 1/f 噪聲，修改後的多尺度熵提供了比傳統樣本熵在典型示例中波動較小的樣本熵曲線。通過對白噪聲和 1/f 噪聲使用 200 個獨立噪聲樣本，每個噪聲樣本包含 500 個數據點，結果顯示，修改後的多尺度熵提供了幾乎與樣本熵相等的熵估計均值，但比樣本熵具有更小的熵估計標準差，表明修改後的多尺度熵和多尺度熵方法在統計上幾乎是等效的；然而，前者方法可以提供比傳統多尺度熵更準確的估計。對真實軸承振動數據的應用也得出了一致的結論。 然而，值得一提的是，考慮到計算成本和對於較長時間序列的有限改進，修改後的多尺度熵不適合直接應用於分析較長時間序列。例如，在[43]中的表 2 中可以看到，對於數據長度為 30 k 的 1/f 噪聲，修改後的多尺度熵提供了幾乎相同的熵估計（包括獨立樣本的平均值和標準差），但需要更高的計算成本。

3.3 Refined Multiscale Entropy
3.3 精煉多尺度熵

The refined multiscale entropy [38] is a method to address two drawbacks of the multiscale entropy: (1) the ‘coarse-graining’ procedure can be considered as applying a finite-impulse response (FIR) filter to the original series x and then downsampling the filtered time series with the scale factor, in which frequency response of the FIR filter can be characterized as a very slow roll-off of the main lobe, large transition band, and important side lobes in the stopband, thus introducing aliasing when the subsequent downsampling procedure is applied; and (2) the parameter r for determining the similarity between two patterns remains constant for all the scales as a percentage of standard deviation of the original time series, thus leading to artificially decreasing entropy rate, as the patterns more likely becomes indistinguishable at higher scale in such a setting.
精煉的多尺度熵[38]是一種解決多尺度熵的兩個缺點的方法：(1)“粗化”過程可以被視為將有限脈衝響應（FIR）濾波器應用於原始序列 x，然後對濾波後的時間序列進行下採樣，其中 FIR 濾波器的頻率響應可以被描述為主瓣的非常緩慢下降、過渡帶較大以及停止帶中重要的側瓣，因此在應用後續下採樣過程時會引入混疊；以及(2)用於確定兩個模式之間相似性的參數 r 對於所有尺度保持不變，作為原始時間序列標準差的百分比，因此在這種設置下，隨著尺度增加，模式更有可能變得難以區分，從而人為地降低熵率。

In order to overcome both shortcomings, the refined multiscale entropy (1) replaced the FIR filter with a low-pass Butterworth filter, whose frequency response was flat in the passband, side lobes in the stopband were not present, and the roll-off was fast, thus ensuring a more accurate elimination of the components and reducing aliasing when the filtered series were downsampled; and (2) let parameter r be continuously updated as a percentage of the standard deviation (SD) of the filtered series, thus compensating the decrease of variance with the elimination of the fast temporal scales.
為了克服這兩個缺點，精煉的多尺度熵（1）將 FIR 濾波器替換為低通 Butterworth 濾波器，其頻率響應在通帶中是平坦的，在阻帶中沒有側瓣，並且下降速度快，從而確保更準確地消除組分並減少當過濾系列被下採樣時的混疊；並且（2）讓參數 r 作為標準差（SD）的百分比不斷更新，從而補償隨著快速時間尺度的消除而降低變異性。

The performance of the refined multiscale entropy was verified and examined by Gaussian white noise, 1/f noise and autoregressive processes, as well as real 24-h Holter recordings of heart rate variability (HRV) obtained from healthy and aortic stenosis (AS) groups. It is worth noting that the results of Gaussian white noise and 1/f noise by the refined multiscale entropy are opposite to those obtained via the multiscale entropy. The main reason leading to this discrepancy is that two methods apply the different calculations of the similarity parameter, r for the coarse-graining procedure. In the original multiscale entropy, the parameter r remains constant for all scale factors as a percentage of standard deviation of the original time series [1], whereas the parameter r in the refined multiscale entropy is continuously updated as a percentage of the standard deviation of the filtered series [38]. It has been pointed out [38] that the coarse-graining procedure in original multiscale entropy eliminates the fast temporal scales as the scale factor increases, acting as a low-pass filter. As such, the coarse-grained series are usually characterized by a lower standard deviation compared to the original time series. Thus, if the parameter r is kept constant for all the scales, more and more patterns will be considered similar with the increasing scale factor, hence increasing estimated regularity and reporting artificially decreasing entropy with the scale factor.
經過對高斯白噪音、1/f 噪音和自回歸過程的驗證和檢驗，以及從健康和主動脈瓣狹窄（AS）組獲得的真實 24 小時 Holter 心率變異性（HRV）記錄，精煉的多尺度熵的表現已得到證實和檢驗。值得注意的是，精煉的多尺度熵對高斯白噪音和 1/f 噪音的結果與通過多尺度熵獲得的結果相反。導致這種差異的主要原因是兩種方法應用了不同的相似性參數 r 的計算，用於粗粒化過程。在原始的多尺度熵中，參數 r 對於所有尺度因子保持不變，作為原始時間序列的標準差的百分比，而在精煉的多尺度熵中，參數 r 作為過濾系列的標準差的百分比持續更新。已指出，在原始的多尺度熵中，粗粒化過程會隨著尺度因子的增加消除快速時間尺度，起到低通濾波器的作用。 因此，粗粒度系列通常具有比原始時間序列更低的標準偏差。因此，如果參數 r 對所有尺度保持恆定，隨著尺度因子的增加，將會有越來越多的模式被認為是相似的，因此估計的規則性將增加，並且隨著尺度因子的增加報告人工降低的熵。

3.4 Generalized Multiscale Entropy
3.4 泛化多尺度熵

The generalized multiscale entropy [44] was developed to generalize the multiscale entropy. In the coarse-graining procedure, a time series was first divided into non-overlapping segments with the length of scale factor, and then the average was taken within each segment, which can been thought as the first moment. Instead of the first moment, the generalized multiscale entropy was proposed to use an arbitrary moment (e.g., volatility when the second moment) to generate the coarse-grained time series for entropy analysis. This approach may offer a new way to explain the calculated entropy results. For instance, when using the second moment, the multiscale entropy represents the multiscale complexity of the volatility of data. This approach has been applied to study cardiac interval time series from three groups, comprising health young and older subjects, and patients with chronic heart failure syndrome [44]. The results show that the complexity indices of healthy young subjects were significantly higher than those of healthy older subjects, whereas the complexity indices of the healthy older subjects were significantly higher than those of the heart failure patients. These results support their hypothesis that the heartbeat volatility time series from healthy young subjects are more complex than those of healthy older subjects, which are more complex than those from patients with heart failure.
廣義多尺度熵[44]是為了擴展多尺度熵而開發的。在粗粒化過程中，首先將時間序列分成不重疊的具有規模因子長度的段，然後在每個段內取平均值，這可以被視為第一時刻。廣義多尺度熵建議使用任意時刻（例如，當第二時刻時使用波動性）來生成用於熵分析的粗粒化時間序列，而不是第一時刻。這種方法可能提供了一種解釋計算熵結果的新途徑。例如，當使用第二時刻時，多尺度熵代表了數據波動性的多尺度複雜性。這種方法已應用於研究來自三組人的心臟間隔時間序列，包括健康的年輕和年長受試者，以及患有慢性心臟衰竭綜合症的患者[44]。結果顯示，健康的年輕受試者的複雜性指數顯著高於健康的年長受試者，而健康的年長受試者的複雜性指數顯著高於心臟衰竭患者的指數。 這些結果支持他們的假設，即來自健康年輕受試者的心跳變動時間序列比來自健康老年受試者的更複雜，而後者比心臟衰竭患者的更複雜。

3.5 Intrinsic Mode Entropy
3.5 內在模態熵

The intrinsic mode entropy [37] identified two shortcomings of the multiscale entropy: (1) the high-frequency components were eliminated by the coarse-graining procedure, which may contain relevant information for some physiological data, and (2) the coarse-graining procedure, while extracting the scales, may be not adapted to nonstationary/nonlinear signal, which is quite common in the physiological systems.
內在模熵[37]指出了多尺度熵的兩個缺點：(1) 高頻成分被粗粒化過程消除，這可能包含一些生理數據的相關信息，以及(2) 粗粒化過程在提取尺度時可能不適應非穩態/非線性信號，這在生理系統中相當常見。

The intrinsic mode entropy was proposed to directly address these issues by exploiting a fully adaptive, data-driven time series decomposition method, namely empirical mode decomposition (EMD) [45], to extract the scales intrinsic to the data. The EMD adaptively decomposes a time series signal, by means of the so-called the sifting method, into a finite set of amplitude- and/or frequency-modulated (AM/FM) modulated components, referred to as intrinsic mode functions (IMFs) [45]. IMFs satisfy the requirements that the mean of the upper and lower envelops is locally zero and the number of extrema and the number of zero-crossing differ by at most one, and thus represent the intrinsic oscillation modes of data on the different frequency scales. By virtue of the EMD, the time series x(t) can be decomposed as x(t)=∑j=1kCj(t)+r(t), where C j (t) , j = 1 ,  …  , k are the IMFs and r(t) is the monotonic residue. The EMD algorithm is briefly described as follows.
內在模態熵是通過利用完全自適應的、數據驅動的時間序列分解方法，即經驗模態分解（EMD）[45]，直接解決這些問題，以提取數據內在的尺度。EMD 通過所謂的篩選方法，自適應地將時間序列信號分解為有限集的幅度和/或頻率調製（AM/FM）調製分量，稱為內在模態函數（IMFs）[45]。IMFs 滿足上下包絡線的平均值在局部為零，極值數和零交叉數之差最多為一，因此代表了不同頻率尺度上數據的內在振蕩模式。通過 EMD，時間序列 x(t)可以分解為 x(t)=∑j=1kCj(t)+r(t) ，其中 C j (t)，j = 1，…，k 是 IMFs，r(t)是單調殘差。EMD 算法簡要描述如下。

  1. 1.

    Let x~(t)=x(t); 讓 x~(t)=x(t) ;

  2. 2.

    Find all local maxima and minima of x~(t);
    找出 x~(t) 的所有局部極大值和極小值；

  3. 3.

    Interpolate through all the minima (maxima) to obtain the lower (upper) signal envelop e min(t) (e max(t));
    通過所有極小值（極大值）進行插值，以獲得下側（上側）信號包絡 e min （t）（e max （t））;

  4. 4.

    Compute the local mean m(t)=emin(t)+emax(t)2;
    計算局部平均值 m(t)=emin(t)+emax(t)2 ;

  5. 5.

    Obtain the detail part of signal c(t)=x~(t)−m(t);
    獲取信號 c(t)=x~(t)−m(t) 的細節部分;

  6. 6.

    Let x~(t)=c(t) and repeat the process from step 2 until c(t) becomes an IMF.
    讓 x~(t)=c(t) 並重複從步驟 2 開始的過程，直到 c(t) 變成 IMF。

Compute the residue r(t) = x(t) − c(t) and go back to step 2 with x~(t)=r(t), until the monotonic residue signal is left.
計算殘差 r(t) = x(t) − c(t) 並回到步驟 2，直到只剩下單調的殘差信號。

As such, in the intrinsic mode entropy, a time series is first adaptively decomposed into several IMFs with distinct frequency bands by EMD, and then the multiple scales of the original signal can be obtained by the cumulative sums of the IMFs, starting from the finest scales and ending with the whole signal, over which the sample entropy is applied. The usefulness of intrinsic mode entropy was demonstrated by its application to real stabilogram signals for discrimination between elderly and control subjects.
因此，在內在模熵中，時間序列首先通過 EMD 自適應分解為幾個具有不同頻段的 IMF，然後通過這些 IMF 的累積和來獲得原始信號的多個尺度，從最細的尺度開始，以整個信號結束，對其應用樣本熵。 內在模熵的實用性通過將其應用於真實的穩定圖信號以區分老年人和對照受試者得到了證明。

It bears noting that relying on the EMD method, the intrinsic mode entropy inevitably suffers from both the mode-misalignment and mode-mixing problems, particularly in the analysis of multivariate time series data [46]. The mode-misalignment refers to a problem where the common frequency modes across a multivariate data appear in the different-index IMFs, thus resulting that the IMFs are not matched either in the number or in scale, whereas the mode-mixing is manifested by a single IMF containing multiple oscillatory modes and/or a single mode residing in multiple IMFs which may in some cases compromise the physical meaning of IMFs and practical applications [47]. Both problems can be simply illustrated by a toy example shown in Fig. 4.2. Because the intrinsic mode entropy is applied to each time series separately, these two problems may contribute to inappropriate operation (e.g., comparison) of entropy values at the ‘same’ scale factor from different time series, for the ‘same’ scale from different time series could be in the largely different frequency ranges.
值得注意的是，依賴 EMD 方法，內在模熵在分析多變量時間序列數據時不可避免地遭受模式不對齊和模式混合問題的困擾[46]。模式不對齊指的是多變量數據中的共同頻率模式出現在不同索引 IMFs 中的問題，導致 IMFs 在數量或尺度上不匹配，而模式混合則表現為單個 IMF 包含多個振蕩模式和/或單個模式存在於多個 IMFs 中，這在某些情況下可能損害 IMFs 的物理含義和實際應用[47]。這兩個問題可以通過圖 4.2 中的一個玩具示例簡單說明。由於內在模熵應用於每個時間序列，這兩個問題可能導致在不同時間序列的“相同”尺度因子上不當操作（例如比較）熵值，因為來自不同時間序列的“相同”尺度可能處於非常不同的頻率範圍。

Fig. 4.2 圖 4.2
figure 2

Example of mode-mixing and mode-misalignment by original empirical mode decomposition
原始經驗模態分解中的模式混合和模式不對齊示例

Full size image 全尺寸圖像

Therefore, an improved intrinsic mode entropy method [46] was introduced to address the potential mode-misalignment and mode-mixing problems based on the multivariate empirical mode decomposition (MEMD), which directly works with multivariate data to greatly mitigate above two problems, generating the aligned IMFs. In this method, the MEMD [48] plays an important role for the extraction of the scales. The MEMD is the multivariate extension of EMD, thus mitigating both mode-misalignment and mode-mixing problems. An important step in the MEMD method, distinct from the EMD, is the calculation of local mean, as the concept of local extrema is not well defined for multivariate signals. To deal with this problem, MEMD projects the multivariate signal along different directions to generate the multiple multidimensional envelops; these envelops are then averaged to obtain the local mean. The details of MEMD can be found in [48]. Figure 4.3 demonstrates the decomposition of same data as in Fig. 4.2 by the MEMD to show that MEMD is effective to produce the aligned IMFs. The application of the improved intrinsic mode entropy approach to real local field potential data from visual cortex of monkeys illustrates that this approach is able to capture more discriminant information than the other methods [49].
因此，引入了改進的內在模熵方法[46]來解決基於多變量經驗模態分解（MEMD）的潛在模式不對齊和混合問題，該方法直接處理多變量數據，從而大大減輕了上述兩個問題，生成了對齊的 IMFs。在這種方法中，MEMD [48]在提取尺度方面發揮了重要作用。MEMD 是 EMD 的多變量擴展，因此可以減輕模式不對齊和混合問題。MEMD 方法中的一個重要步驟，與 EMD 不同的是，是計算局部均值，因為對於多變量信號，局部極值的概念並不明確。為了應對這個問題，MEMD 將多變量信號投影到不同方向以生成多個多維包絡；然後將這些包絡平均以獲得局部均值。MEMD 的詳細信息可以在[48]中找到。圖 4.3 展示了通過 MEMD 對與圖 4.2 中相同的數據進行分解，以顯示 MEMD 能夠有效生成對齊的 IMFs。 將改進的固有模熵方法應用於猴子視覺皮層的真實局部場電位數據，顯示這種方法能夠捕捉比其他方法更多的可區分信息。

Fig. 4.3 圖 4.3
figure 3

Decomposition of same data in Fig. 4.2 by multivariate empirical mode decomposition (MEMD), showing the aligned decomposed components
透過多變量經驗模態分解（MEMD）在圖 4.2 中分解相同數據，顯示對齊的分解組件。

Full size image 全尺寸圖像

Thus far, the EMD family has been extensively used in multiscale entropy analysis [41, 50]. It should be noted that one important extension of EMD, ensemble EMD [47], has also been applied to multiscale entropy method to solve the mode-mixing problem [51, 52]. However, the aligned IMF numbers from different time series are not guaranteed by this method. In addition, to preserve the high frequency component in entropy analysis, the hierarchical entropy was used essentially based on wavelet decomposition [53], which is effective for the analysis of nonstationary time series data.
到目前為止，EMD 家族已被廣泛應用於多尺度熵分析。值得注意的是，EMD 的一個重要擴展，即集成 EMD，也已應用於多尺度熵方法以解決模態混合問題。然而，這種方法並不能保證來自不同時間序列的對齊 IMF 數量。此外，為了在熵分析中保留高頻成分，基本上使用了基於小波分解的分層熵，對於非穩態時間序列數據的分析是有效的。

3.6 Adaptive Multiscale Entropy
3.6 自適應多尺度熵

The adaptive multiscale entropy (AME) [35] was developed to provide a comprehensive means for the scales extracted from time series including both the ‘coarse-to-fine’ and ‘fine-to-coarse’ scales. The method was specifically to address the issue of multiscale entropy that the high frequency component is eliminated. With the AME, the scale extraction is adaptive, completely driven by the data via EMD, thus suitable for nonstationary/nonlinear time series data. Moreover, by employing the multivariate extension of empirical mode decomposition (i.e., MEMD), the proposed AME can fully address the mode-misalignment and mode-mixing problems induced by univariate empirical mode decomposition for the analysis of individual time series, thus producing the aligned IMF components and ensuring proper operations (e.g., comparison) of entropy estimation at one scale over multiple time series data.
自適應多尺度熵（AME）[35]的開發旨在提供一種全面的方法，用於從時間序列中提取包括“粗到細”和“細到粗”尺度的尺度。該方法專門解決了多尺度熵中高頻成分被消除的問題。通過 AME，尺度提取是自適應的，完全由 EMD 通過數據驅動，因此適用於非平穩/非線性時間序列數據。此外，通過使用經驗模態分解的多變量擴展（即 MEMD），所提出的 AME 可以完全解決單變量經驗模態分解引起的模態不對齊和模態混合問題，用於分析單個時間序列，從而生成對齊的 IMF 成分並確保在多個時間序列數據上的一個尺度上進行熵估計的正確操作（例如比較）。

To implement the AME, the MEMD method is first applied to decompose data into the aligned IMFs. The scales are then selected by consecutively removing either the high-frequency or low-frequency IMFs from the original data. The way to select the scales results in two algorithms, namely the fine-to-coarse AME and the coarse-to-fine AME, which essentially represent the multiscale low-pass and high-pass filtering of the original signal, respectively. The sample entropy is applied to the selective scales to estimate the entropy measure. When applying this approach to physiological time series signal (e.g., neural data), two issues [49] had to be solved: (1) the physiological data are often collected over certain time period from multiple channels across many trials, which can be represented as a three-dimensional matrix, i.e. TimePoints × Channels × Trials, thus not directly solvable by the MEMD; and (2) the physiological recordings are usually collected over many trials spanning from days to months, or even years, so that the dynamic ranges of multiple signals are likely to be of high degree of variability, which can have detrimental effect upon the final decomposition of MEMD. Therefore, the AME adopts two important preprocessing steps to accommodating the multivariate data. First, the high-dimensional physiological data (e.g. TimePoints × Channels × Trials) is first reshaped into such a two-dimensional time series as TimePoints × [Channels × Trials] before subject to the MEMD analysis. It is an important step to make sure that all the IMFs be aligned not only across channels, but also across trials. Second, in order to reduce the variability among neural recordings, individual time series in the reshaped matrix is normalized against their temporal standard deviation before the MEMD is applied. After the MEMD decomposition, those extracted standard deviations are then restored to the corresponding IMFs.
實施 AME 時，首先應用 MEMD 方法將數據分解為對齊的 IMFs。然後通過連續刪除原始數據中的高頻或低頻 IMFs 來選擇尺度。選擇尺度的方式導致了兩種算法，即從精細到粗糙的 AME 和從粗糙到精細的 AME，它們本質上代表了原始信號的多尺度低通和高通過濾。樣本熵應用於選擇性尺度以估計熵度量。當將此方法應用於生理時間序列信號（例如神經數據）時，必須解決兩個問題[49]：（1）生理數據通常在一定時間段內從多個通道跨越多個試驗收集，可以表示為三維矩陣，即時間點×通道×試驗，因此無法直接通過 MEMD 解決；（2）生理記錄通常在許多試驗中收集，跨越從幾天到幾個月，甚至幾年，因此多個信號的動態範圍可能具有高度變異性，這可能對 MEMD 的最終分解產生不利影響。 因此，AME 採用兩個重要的預處理步驟來應對多變數數據。首先，將高維生理數據（例如時間點×通道×試驗）首先重塑為二維時間序列，即時間點×[通道×試驗]，然後再進行 MEMD 分析。這是一個重要的步驟，以確保所有 IMFs 不僅在通道之間對齊，而且在試驗之間也對齊。其次，為了減少神經記錄之間的變異性，重塑矩陣中的個別時間序列在應用 MEMD 之前根據它們的時間標準差進行了標準化。在 MEMD 分解之後，這些提取的標準差然後被恢復到相應的 IMFs 中。

Simulations demonstrate that the AME is able to adaptively extract the scales inherent in the nonstationary signal and that the AME works with both the coarse scales and fine scales in the data [35]. The application to real local field potential data in the visual cortex of monkeys suggests that the AME is suitable for entropy analysis of nonlinear/nonstationary physiological data, and outperforms the multiscale entropy in revealing the underlying entropy information retained in the intrinsic scales. The AME method has been further extended as adaptive multiscale cross-entropy (AMCE) [49] to assess the nonlinear dependency between time series signals. Both the AME and AMCE are employed to neural data from the visual cortex of monkeys to explore how the perceptual suppression is reflect by neural activity within individual brain areas and functional connectivity between areas.
模擬顯示，AME 能夠自適應地提取非穩態信號中固有的尺度，並且 AME 能夠處理數據中的粗尺度和細尺度。應用於猴子視覺皮層的真實局部場電位數據表明，AME 適用於非線性/非穩態生理數據的熵分析，並且在揭示內在尺度中保留的熵信息方面優於多尺度熵。AME 方法已進一步擴展為自適應多尺度交叉熵（AMCE），用於評估時間序列信號之間的非線性依賴性。AME 和 AMCE 均應用於猴子視覺皮層的神經數據，以探索感知抑制如何通過個別腦區內的神經活動和腦區之間的功能連接來反映。

4 Methods for Entropy Estimation
熵估計的四種方法

4.1 Multiscale Permutation Entropy
4.1 多尺度排列熵

The permutation entropy [54], instead of the sample entropy, has been applied to conduct the multiscale entropy analysis [55]. By using the rank order value of embedded vector, the permutation entropy is robust for the time series with nonlinear distortion, and is also computationally efficient. Specifically, with the m-dimensional delay, the original time series is transformed into a set of embedded vectors. Each vector is then represented by its rank order. For instance, a vector, [12, 56, 0.0003, 100,000, 50] can be represented by its rank order, [1,2,3,4,5]. We can see that the rank order is insensitive to the magnitude of the data, though the values may be at largely different scales. Subsequently, for a given embedded dimension (e.g., m dimension), the rate of each possible rank order, out of m! possible rank orders, is calculated over all the embedded vectors, forming a probability distribution over all the rank orders. The Shannon entropy is finally applied to the probability distribution to obtain the entropy estimation.
排列熵[ 54]，而不是樣本熵，已被應用於進行多尺度熵分析[ 55]。通過使用嵌入向量的等級順序值，排列熵對於具有非線性失真的時間序列是穩健的，並且在計算上也是高效的。具體而言，使用 m 維延遲，將原始時間序列轉換為一組嵌入向量。然後，每個向量由其等級順序表示。例如，一個向量，[12, 56, 0.0003, 100,000, 50]可以通過其等級順序[ 1, 2, 3, 4, 5]表示。我們可以看到，等級順序對於數據的大小是不敏感的，儘管值可能在非常不同的尺度上。隨後，對於給定的嵌入維度（例如，m 維度），在所有嵌入向量上計算每個可能等級順序的比率，形成所有等級順序的概率分佈。最終，Shannon 熵應用於概率分佈以獲得熵估計。

In the similar fashion, the multiscale symbolic entropy [56] was developed to reliably assess the complexity in noisy data while being highly resilient to outliers. In the time series data, the outliers are often illustrated as those data points with the significantly higher or lower magnitudes than most of data points due to some internal/external uncontrolled influence. In this approach, the variation at a time point consists of both the magnitude (absolute value) and the direction (sign). It is hypothesized that dynamics in the sign time series can adequately reflect the complexity in raw data and that the complexity estimation based on the sign time series is more resilient to outliers as compared to raw data. To implement this method, the original time series at a given scale is first divided into non-overlapped segments, within each of which the median is calculated to generate a coarse-grained time series. The sign time series of the coarse grained signal is then generated by considering the direction of change at each point (i.e., 1 for increasing and 0 otherwise). The discrete probability count and the Shannon entropy are applied to the sign data to obtain the entropy estimation. The multiscale measure is obtained when the above procedure goes over all the predefined scales. This method has been successfully applied to the analysis of human heartbeat recordings, showing the robustness to noisy data with outliers.
以類似方式，多尺度符號熵[56]被開發出來，以可靠地評估嘈雜數據中的複雜性，同時對異常值具有高度的韌性。在時間序列數據中，異常值通常被描述為那些由於某些內部/外部無法控制的影響而具有明顯較高或較低幅度的數據點。在這種方法中，某一時間點的變化包括幅度（絕對值）和方向（符號）。假設符號時間序列中的動態可以充分反映原始數據中的複雜性，並且基於符號時間序列的複雜性估計相對於原始數據更具韌性。為了實施這種方法，首先將給定尺度的原始時間序列分為非重疊的段，在每個段內計算中位數以生成粗粒化的時間序列。然後通過考慮每個點的變化方向（即，增加為 1，否則為 0）來生成粗粒化信號的符號時間序列。 將離散概率計數和 Shannon 熵應用於符號數據以獲得熵估計。當上述程序遍歷所有預定義的尺度時，將獲得多尺度測量。該方法已成功應用於人類心跳記錄的分析，展示對帶有離群值的嘈雜數據的穩健性。

4.2 Multiscale Compression Entropy
4.2 多尺度壓縮熵

The multiscale compression entropy [57] has been reported, which replaced the sample entropy with the compression entropy [58] to conduct the multiscale entropy analysis. The basic idea of compression entropy is the smallest algorithm that produces a string is the entropy of that string from algorithmic information theory, which can be approximated by the data compression techniques. For instance, the compression entropy per symbol can be represented by the ratio of compressed text to the original text length, if the length of the text to be compressed is sufficiently large and if the source is an ergodic process. The compression entropy provides an indication to which degree the time series under study can be compressed using the detection of recurring sequences. The more frequent the occurrences of sequences (and thus, the more regular the time series), the higher the compression rate. The ratio of the lengths of the compressed to the uncompressed time series is used as a complexity measure and identified as compression entropy. The multiscale compression entropy exploits the coarse-graining procedure to generate the scales of data, over which the compression entropy is applied. This approach has been applied to the entropy analysis for the microvascular blood flow signals [57]. In this application, microvascular blood flow was continuously monitored with laser speckle contrast imaging (LSCI) and with laser Doppler flowmetry (LDF) simultaneously from healthy subjects. The results show that, for both LSCI and LDF time series, the compression entropy values are less than 1 for all of the scales analyzed, suggesting that there are repetitive structures within the data fluctuations at all scales.
多尺度壓縮熵[57]已被報導，它將樣本熵替換為壓縮熵[58]以進行多尺度熵分析。壓縮熵的基本思想是生成一個字符串的最小算法是該字符串的熵，可以通過數據壓縮技術來近似。例如，每個符號的壓縮熵可以通過壓縮文本與原始文本長度的比率來表示，如果要壓縮的文本長度足夠大且源是遞歸過程。壓縮熵提供了一個指示，表明研究中的時間序列可以使用檢測重複序列來進行壓縮的程度。序列的出現越頻繁（因此，時間序列越規則），壓縮率就越高。壓縮後的時間序列與未壓縮時間序列的長度比被用作複雜度度量並被識別為壓縮熵。多尺度壓縮熵利用粗粒化程序生成數據的尺度，並在這些尺度上應用壓縮熵。 這種方法已應用於微血管血流信號的熵分析[57]。在這個應用中，微血管血流使用激光散斑對比成像（LSCI）和激光多普勒流量計（LDF）同時從健康受試者中進行連續監測。結果顯示，對於 LSCI 和 LDF 時間序列，所有分析尺度的壓縮熵值均小於 1，表明在所有尺度上數據波動中存在重複結構。

4.3 Fuzzy Entropy 4.3 模糊熵

In the family of approximate entropy [5], for example, sample entropy [6], the similarity of vectors (or patterns) from a time series is a key component for accurate estimation of entropy. The sample entropy (and approximate entropy) assesses the similarity between vectors based on the Heaviside function, as shown in Fig. 4.4. It is evident that the boundary of Heaviside function is rigid, which leads to that all the data points inside boundary are treated equally, whereas the data points outside the boundary are excluded no matter how close this point locates to boundary. Thus, the estimation of sample entropy is highly sensitive to the change of the tolerance, r or data point location.
在近似熵家族中，例如樣本熵，從時間序列中的向量（或模式）的相似性是準確估計熵的關鍵組成部分。樣本熵（和近似熵）根據 Heaviside 函數評估向量之間的相似性，如圖 4.4 所示。顯然，Heaviside 函數的邊界是剛性的，這導致邊界內的所有數據點被平等對待，而在邊界之外的數據點則被排除，無論這個點距離邊界多近。因此，樣本熵的估計對於容忍度、r 或數據點位置的變化非常敏感。

Fig. 4.4 圖 4.4
figure 4

Heaviside function (dash dotted black) and fuzzy function (solid blue) for similarity in entropy estimation (modified based on [21]. As figure shown, by the Heaviside function, both points d2 (red) and d3 (red) are considered within the boundary and both similar to the original point (i.e., ‘0’); whereas another point d1 (green), very close to d2 though, is considered dissimilar because it falls just outside the boundary. Thus a slight increase in r will make the boundary encloses the point d1, and then the conclusion totally changes. However, the fuzzy function will largely relieve this issue
Heaviside 函數（虛線黑色）和模糊函數（實線藍色）用於熵估計中的相似性（基於[21]修改）。如圖所示，通過 Heaviside 函數，點 d2（紅色）和 d3（紅色）都被認為在邊界內並且與原始點相似（即‘0’）；而另一個點 d1（綠色），雖然非常接近 d2，但被認為不相似，因為它剛好落在邊界之外。因此，稍微增加 r 將使邊界包圍點 d1，然後結論完全改變。然而，模糊函數將大大緩解這個問題。

Full size image 全尺寸圖像

The fuzzy entropy [36] aimed to improve the entropy estimation at just this point, based on the concept of fuzzy sets [59], which adopted the “membership degree” with a fuzzy function that associates each point with a real number in a certain range (e.g., [0, 1]). The fuzzy entropy employed the family of exponential function as the fuzzy function to obtain the fuzzy measurement of similarity, which bears two desired properties: (1) being continuous so that the similarity does not change abruptly; (2) being convex so that the self-similarity is the maximum. In addition, the fuzzy entropy removes the baseline of the vector sequences, so that the similarity measure more relies on vectors’ shapes rather than their absolute coordinates, which makes the similarity definition fuzzier.
模糊熵[36]旨在改善熵估計的這一點，基於模糊集合[59]的概念，採用“隸屬度”與模糊函數，將每個點與某個範圍內的實數（例如，[0, 1]）關聯起來。模糊熵採用指數函數家族作為模糊函數，以獲得相似性的模糊測量，具有兩個期望的特性：（1）連續性，使相似性不會突然改變；（2）凸性，使自相似性達到最大。此外，模糊熵消除了向量序列的基線，使相似性度量更依賴於向量的形狀而不是它們的絕對坐標，從而使相似性定義更加模糊。

Extensive simulations and application [60] to experimental electromyography (EMG) suggest that the fuzzy entropy is a more accurate entropy measure than the approximate entropy and sample entropy, and exhibits the stronger relative consistency and less dependence on the data length, thus providing an improved evaluation of signal complexity, especially for short time series contaminated by noise. For instance, as shown from the Fig. 4.2 in [60], with only 50 data samples, the fuzzy entropy can successfully discriminate three periodical sinusoidal time series with different frequencies, outperforming the approximate entropy and sample entropy. And from the Fig. 5 in [60], it is observed that the fuzzy entropy can consistently separate the different logistic datasets contaminated by noises with different noise levels, while it becomes difficult for the approximate entropy and sample entropy to distinguish those data. In addition to the exponential function, the nonlinear sigmoid and Gaussian functions have also been used to replace the Heaviside function for similarity measure [61]. The fuzzy entropy was also extended to cross-fuzzy entropy to test nonlinear pattern synchrony of bivariate time series [62]. It has been shown that the fuzzy entropy can be also used in the multiscale entropy analysis by replacing the sample entropy [63, 64].
廣泛的模擬和應用[60]到實驗性肌電圖（EMG）表明，模糊熵是比近似熵和樣本熵更準確的熵度量，並且表現出更強的相對一致性和對數據長度的依賴性較小，因此提供了對信號複雜性的改進評估，特別是對受噪聲干擾的短時間序列。例如，如[60]中的圖 4.2 所示，僅使用 50 個數據樣本，模糊熵可以成功區分具有不同頻率的三個周期正弦時間序列，優於近似熵和樣本熵。從[60]中的圖 5 可以觀察到，模糊熵可以一致地區分不同噪聲水平的不同邏輯數據集，而近似熵和樣本熵很難區分這些數據。除了指數函數外，非線性 Sigmoid 和高斯函數也已被用來替換 Heaviside 函數進行相似性度量[61]。 模糊熵也被擴展為交叉模糊熵，以測試雙變量時間序列的非線性模式同步。已經證明，模糊熵也可以通過替換樣本熵在多尺度熵分析中使用。

4.4 Multivariate Multiscale Entropy
4.4 多變量多尺度熵

The multivariate multiscale entropy [65] was introduced to perform entropy analysis for multivariate time series, which has been increasingly common for physiological data due to the advance in recording techniques. The multivariate multiscale entropy adopts the coarse-graining procedure to extract the scales of data, and then extends the sample entropy algorithm to multivariate sample entropy for entropy estimation of coarse-grained multivariate data. The detailed multivariate sample entropy algorithm can be found in [65]. The simulations and a large array of real-world applications [66] including the human stride interval fluctuations data, cardiac interbeat interval and respiratory interbreath interval data, 3D ultrasonic anemometer data taken in the north-south, east-west, and vertical directions etc., have demonstrated the effectiveness of this approach in assessing the underlying dynamics of multivariate time series.
多變量多尺度熵[65]被引入以進行多變量時間序列的熵分析，這在生理數據中越來越常見，這是由於記錄技術的進步。多變量多尺度熵採用粗粒化程序來提取數據的尺度，然後擴展樣本熵算法以用於粗粒化多變量數據的熵估計。詳細的多變量樣本熵算法可以在[65]中找到。模擬和大量的真實應用[66]，包括人類步幅間隔波動數據、心臟間拍間隔和呼吸間呼吸間隔數據，以及在南北、東西和垂直方向進行的 3D 超聲風速計數據等，已經證明了這種方法在評估多變量時間序列的潛在動態方面的有效性。

It is worth to mention that copula can be used to implement multivariate multiscale entropy by incorporating the multivariate empirical mode decomposition and the Renyi entropy [67]. The Renyi entropy (or information) is a probability-based unified entropy measure, which is considered to generalize the Hartley entropy, the Shannon entropy, the collision entropy and the min-entropy. The Renyi entropy has been shown as a robust (multivariate) entropy estimation when its implementation algorithm is based on the copula of multivariate distribution [67]. The copula [68, 69] can be considered as the transformation which standardizes the marginal of multivariate data to be uniform on [0, 1] while preserving many of the distribution’s dependence properties including its concordance measures and its information, which has been widely recognized in many fields, e.g., finance [70, 71], physiology [72,73,74], etc. Thus, the Renyi entropy estimation is based entirely on the ranks of multivariate data, therefore robust to outliers. As such, the application of Renyi entropy to the adaptively extracted scales of multivariate data by the multivariate empirical mode decomposition may provide a potential option to implement multivariate multiscale entropy.
值得一提的是，連結詞可以用來實現多變量多尺度熵，通過結合多變量經驗模態分解和 Renyi 熵[67]。 Renyi 熵（或信息）是一種基於概率的統一熵度量，被認為是對 Hartley 熵、Shannon 熵、碰撞熵和最小熵進行泛化。當實現算法基於多變量分佈的連結詞時，Renyi 熵被證明是一種強健（多變量）熵估計[67]。 連結詞[68,69]可以被視為將多變量數據的邊際標準化為[0,1]上的均勻分佈的轉換，同時保留許多分佈的相依性屬性，包括其一致性度量和信息，這在許多領域中被廣泛認可，例如金融[70,71]、生理學[72,73,74]等。因此，Renyi 熵估計完全基於多變量數據的排名，因此對異常值具有強健性。 因此，將 Renyi 熵應用於多變量實驗模態分解自適應提取的尺度，可能提供實現多變量多尺度熵的潛在選擇。

The above multivariate entropy methods all assess the simultaneous dependency for multivariate data, while the transfer entropy [75] has been developed to measure the directed information transfer between time series, revealing a causal relationship between signal rather than correlation. The multiscale transfer entropy [76] makes use of the wavelet-based method to extract multiple scales of data, and then measure directional transfer of information between coupled systems at the multiple scales. This approach has demonstrated its effectiveness by extensive simulations and application to real physiological (heart beat and breathe) and robotic (composed of one sensor and one actuator) data.
上述的多變量熵方法都評估多變量數據的同時依賴性，而轉移熵[75]已被發展出來用於測量時間序列之間的定向信息傳輸，揭示信號之間的因果關係而不是相關性。多尺度轉移熵[76]利用基於小波的方法提取多個尺度的數據，然後在多個尺度上測量耦合系統之間的信息定向傳輸。這種方法通過廣泛的模擬和應用於真實生理（心跳和呼吸）和機器人（由一個傳感器和一個致動器組成）數據已經證明了其有效性。

5 Multiscale Entropy Analysis of Cardiovascular Time Series
心血管時間序列的 5 種多尺度熵分析

Nonlinear analysis of cardiovascular data has been widely recognized to provide relevant information on psychophysiological and pathological states. Among others, entropy measure has been serving as a powerful tool to quantify the cardiovascular dynamics of a time series over multiple time scales [1] through approximate entropy [5], sample entropy [6] and multiscale entropy [1]. When the multiscale entropy was initially developed, it has been applied to analysis of heart beat signal for diagnostics, risk stratification, detection of toxicity of cardiac drugs and study of intermittency in energy and information flows of cardiac system [1, 44, 77]. In the original publication for the sample entropy [1], the multiscale entropy was applied to analyze the heartbeat intervals time series from (1) healthy subjects, (2) subjects with congestive heart failure, and (3) subjects with the atrial fibrillation. The analysis results of multiscale entropy show that at scale of 20 (note not the original scale) the entropy value for the coarse-grained time series derived from healthy subjects is significantly higher than those for atrial fibrillation and congestive heart failure, facilitating to address the longstanding paradox for the applications of traditional single-scale entropy methods to physiological time series, that is, the traditional entropy methods may yield the higher complexity for certain pathologic processes associated with random outputs than that for healthy dynamics exhibiting long-range correlations, but it is believed that disease states or aging may be defined by a sustained breakdown of long-range correlations and thus loss of information, i.e., less complexity. This work suggests that the paradox may be due to the fact that conventional algorithms fail to account for the multiple time scales inherent in physiologic dynamics, which can be discovered by the multiscale entropy. In addition, the multiscale entropy has been applied, but not limited, to analysis of heart rate variability for the objective quantification of psychological traits through autonomic nervous system biomarkers [78], detection of cardiac autonomic neuropathy [79] and assessing the severity of sleep disordered breathing [80], to analysis of microvascular blood flow signal for better understanding of the peripheral cardiovascular system [57], to analysis of interval variability from Q-waveonset to T-wave end (QT) derived from 24-hour Holter recordings for improving identification of condition of the long QT syndrome type 1 [81] and to analysis of pulse wave velocity signal for differentiating among healthy, aged, and diabetic populations [42]. A typical example of application of multiscale entropy to the heart rate variability analysis [80] is to investigate the relationship between the obstructive sleep apnea (OSA) and the complexity of heart rate variability to identify the predictive value of the heart rate variability analysis in assessing the severity of OSA. In the study, the R-R intervals from 10 segments of 10-min electrocardiogram recordings during non-rapid eye movement sleep at stage N2 were collected from four groups of subjects: (1) the normal snoring subjects without OSA, (2) mild OSA, (3) moderate OSA and (4) severe OSA. The multiscale entropy was applied to perform the heart rate variability analysis, in which the multiple scales were divided into the small scale (scale 1–5) and the large scale (scale 6–10). The analysis results show that the entropy at the small scale could successfully distinguish the normal snoring group and the mild OSA group from the moderate and severe groups, and a good correlation between the entropy at the small scale and the apnea hypopnea index was displayed, suggesting that the multiscale entropy analysis at the small scale may serve as a simple preliminary screening tool for assessing the severity of OSA. Except the heart rate variability signal, the multiscale entropy has been proved as a powerful analysis tool for many other physiological signals, e.g., for analysis of pulse wave velocity signal [42]. In the study, the pulse wave velocity series were recorded from 4 groups of subjects: (1) the healthy young group, (2) the middle-aged group without known cardiovascular disease, (3) the middle-aged group with well-controlled diabetes mellitus type 2 and (4) the middle-aged group with poorly-controlled diabetes mellitus type 2. By applying the multiscale entropy analysis, the results show that the multiscale entropy can produce significant differences in entropies between the different groups of subjects, demonstrating a promising biomarker for differentiating among healthy, aged, and diabetic populations. It is worth to mention that an interesting frontier in nonlinear analysis on heart rate variability (HRV) data was represented by the assessment of psychiatric disorders. Specifically, multiscale entropy was performed on the R-R interval series to assess the heartbeat complexity as an objective clinical biomarker for mental disorders [82]. In the study, the R-R interval data were acquired from the bipolar patients who exhibited mood states among depression, hypomania, and euthymia. Multiscale entropy analysis was applied to the heart rate variability to discriminate the three pathological mood states. The results show that the euthymic state is associated to the significantly higher complexity at all scales than the depressive and hypomanic states, suggesting a potential utilization of the heart rate variability complexity indices for a viable support to the clinical decision. Recently, an instantaneous entropy measure based on the inhomogeneous point-process theory is an important methodological advance [83]. This novel measure has been successfully used for analyzing heartbeat dynamics of healthy subjects and patients with cardiac heart failure together with gait recordings from short walks of young and elderly subjects. It therefore offers a promising mathematical tool for the dynamic analysis of a wide range of applications and to potentially study any physical and natural stochastic discrete processes [84]. With the further advance of multiscale entropy method, it is expected that this method will make much more contributions in discovering the nonlinear structure properties in cardiac systems.
心血管數據的非線性分析被廣泛認為提供有關心理生理和病理狀態的相關信息。在其他方法中，熵度量一直作為一種強大的工具，通過近似熵、樣本熵和多尺度熵來量化時間序列的心血管動態。當多尺度熵最初被開發時，它已被應用於心跳信號的分析，用於診斷、風險分層、檢測心臟藥物的毒性以及研究心臟系統的能量和信息流的間歇性。在樣本熵的原始出版物中，多尺度熵被應用於分析（1）健康受試者、（2）患有充血性心力衰竭的受試者和（3）患有心房顫動的受試者的心跳間隔時間序列。 多尺度熵分析結果顯示，在尺度為 20（注意不是原始尺度）時，從健康受試者衍生的粗粒化時間序列的熵值顯著高於房顫和充血性心力衰竭的熵值，有助於解決傳統單尺度熵方法應用於生理時間序列時的長期悖論，即傳統熵方法可能對某些與隨機輸出相關的病理過程產生更高的複雜性，而不是對表現出長程相關的健康動態產生更高的複雜性，但人們認為疾病狀態或衰老可能被長程相關的持續破壞和信息丟失所定義，即較低的複雜性。這項研究表明，這種悖論可能是因為傳統算法未能考慮生理動態中固有的多個時間尺度，而這可以通過多尺度熵來發現。 此外，多尺度熵已被應用於心率變異性的分析，以客觀量化心理特徵通過自主神經系統生物標記物[78]，檢測心臟自主神經病變[79]和評估睡眠呼吸紊亂的嚴重程度[80]，分析微血管血流信號以更好地理解外周心血管系統[57]，分析從 24 小時 Holter 記錄中衍生的 Q 波起始到 T 波結束（QT）的間隔變異性，以改善長 QT 綜合症 1 型的狀況識別[81]，以及分析脈搏波速度信號以區分健康、老年和糖尿病人群[42]。多尺度熵應用於心率變異性分析的典型例子[80]是研究阻塞性睡眠呼吸暫停（OSA）與心率變異性複雜性之間的關係，以確定心率變異性分析在評估 OSA 嚴重程度中的預測價值。 在這項研究中，從四組受試者收集了 10 分鐘非快速眼動睡眠 N2 期間的 10 個段的 R-R 間隔的心電圖記錄：（1）沒有睡眠呼吸暫停症的正常打鼾受試者，（2）輕度睡眠呼吸暫停症，（3）中度睡眠呼吸暫停症和（4）嚴重睡眠呼吸暫停症。多尺度熵被應用於進行心率變異性分析，其中多個尺度被劃分為小尺度（尺度 1-5）和大尺度（尺度 6-10）。分析結果顯示，小尺度的熵能夠成功區分正常打鼾組和輕度睡眠呼吸暫停組與中度和嚴重組，並且小尺度的熵與呼吸暫停低通氣指數之間有良好的相關性，表明小尺度的多尺度熵分析可能作為評估睡眠呼吸暫停症嚴重程度的簡單初步篩查工具。除了心率變異性信號外，多尺度熵已被證明是許多其他生理信號的強大分析工具，例如，用於脈搏波速度信號的分析。 在這項研究中，從 4 組受試者中記錄了脈搏波速度序列：（1）健康年輕組，（2）無已知心血管疾病的中年組，（3）糖尿病 2 型得到良好控制的中年組，以及（4）糖尿病 2 型得到不良控制的中年組。通過應用多尺度熵分析，結果顯示多尺度熵能夠在不同組別的受試者之間產生顯著的熵差異，展示了一種有望區分健康、老年和糖尿病人群的生物標誌物。值得一提的是，非線性分析在心率變異性（HRV）數據中的一個有趣前沿是對精神疾病的評估。具體來說，對 R-R 間隔序列進行多尺度熵分析，以評估心跳複雜性作為精神疾病的客觀臨床生物標誌物。在這項研究中，從表現出抑鬱、輕躁和情緒穩定三種情緒狀態的躁鬱症患者中獲取了 R-R 間隔數據。 多尺度熵分析被應用於心率變異性以區分三種病理情緒狀態。結果顯示，情感穩定狀態在所有尺度上的複雜度顯著高於抑鬱和輕躁狀態，暗示心率變異性複雜度指標可能對臨床決策提供可行支持。最近，基於不均勻點過程理論的瞬時熵測量是一項重要的方法進步。這種新穎的測量已成功應用於分析健康受試者和心臟衰竭患者的心跳動態，以及年輕和老年受試者短距離步行的步態記錄。因此，它為廣泛應用的動態分析提供了一個有前途的數學工具，並有可能研究任何物理和自然隨機離散過程。隨著多尺度熵方法的進一步發展，預計這種方法將在發現心臟系統中的非線性結構特性方面做出更多貢獻。

6 Conclusion 結論

This systematic review summarizes the multiscale entropy and its many variations mainly from two perspectives: (1) the extraction of multiple scales, and (2) the entropy estimation methods. These methods are designed to improve the accuracy and precision of the multiscale entropy method, especially when the time series is short and noisy. Given a large cohort of multiscale entropy methods rapidly developed within the past decade, it becomes clear that the multiscale entropy is an emerging technique that can be used to evaluate the relationship between complexity and health in a number of physiological systems. This can be seen, for instance, in the analysis of cardiovascular time series with the multiscale entropy measure. It is our hope that this review may serve as a reference to the development and application of multiscale entropy methods, to better understand the pros and cons of this methodology, and to inspire new ideas for further development for years to come.
這篇系統性回顧主要從兩個角度總結了多尺度熵及其許多變體：(1)多尺度提取，以及(2)熵估計方法。這些方法旨在提高多尺度熵方法的準確性和精確性，特別是在時間序列短且嘈雜的情況下。考慮到過去十年內迅速發展的大量多尺度熵方法，顯然多尺度熵是一種新興技術，可用於評估多種生理系統中複雜性與健康之間的關係。例如，在心血管時間序列分析中使用多尺度熵測量。我們希望這篇回顧可以作為多尺度熵方法的發展和應用的參考，以更好地了解這種方法的優缺點，並激發未來幾年進一步發展的新思路。