For the 36th Time… the Latest from Our R&D Pipeline
第 36 次......来自我们研发管道的最新消息
Today we celebrate the arrival of the 36th (x.x) version of the Wolfram Language and Mathematica: Version 14.1. We’ve been doing this since 1986: continually inventing new ideas and implementing them in our larger and larger tower of technology. And it’s always very satisfying to be able to deliver our latest achievements to the world.
今天,我们庆祝 Wolfram 语言和 Mathematica 的第 36 个 (x.x) 版本的到来:版本 14.1。自 1986 年以来,我们一直在这样做:不断发明新想法,并将其应用到我们越来越大的技术塔中。能够向全世界展示我们的最新成果,我们总是感到非常满足。
We released Version 14.0 just half a year ago. And—following our modern version scheduling—we’re now releasing Version 14.1. For most technology companies a .1 release would contain only minor tweaks. But for us it’s a snapshot of what our whole R&D pipeline has delivered—and it’s full of significant new features and new enhancements.
就在半年前,我们发布了 14.0 版。现在,我们按照现代版本计划发布了 14.1 版。对于大多数技术公司而言,.1 版本仅包含一些微小的调整。但对于我们来说,这是我们整个研发管道所交付成果的一个缩影,其中包含了大量重要的新功能和新的增强功能。
If you’ve been following our livestreams, you may have already seen many of these features and enhancements being discussed as part of our open software design process. And we’re grateful as always to members of the Wolfram Language community who’ve made suggestions—and requests. And in fact Version 14.1 contains a particularly large number of long-requested features, some of which involved development that has taken many years and required many intermediate achievements.
如果您一直关注我们的现场直播,您可能已经看到我们在开放式软件设计过程中讨论了许多这些功能和增强功能。我们一如既往地感谢 Wolfram 语言社区成员提出的建议和要求。事实上,14.1 版本包含了大量长期以来一直被要求的功能,其中一些功能的开发耗时多年,需要取得许多中间成果。
There’s lots of both extension and polishing in Version 14.1. There are a total of 89 entirely new functions—more than in any other version for the past couple of years. And there are also 137 existing functions that have been substantially updated. Along with more than 1300 distinct bug fixes and specific improvements.
14.1 版既有大量扩展功能,也有大量改进功能。总共有 89 个全新的功能,比过去几年的任何版本都要多。此外,还有 137 项现有功能得到了大幅更新。此外,还有 1300 多个不同的错误修复和具体改进。
Some of what’s new in Version 14.1 relates to AI and LLMs. And, yes, we’re riding the leading edge of these kinds of capabilities. But the vast majority of what’s new has to do with our continued mission to bring computational language and computational knowledge to everything. And today that mission is even more important than ever, supporting not only human users, but also rapidly proliferating AI “users”—who are beginning to be able to routinely make even broader and deeper use of our technology than humans.
14.1 版中的一些新功能与人工智能和LLMs有关。是的,我们正处于这些功能的前沿。但是,绝大多数新功能都与我们将计算语言和计算知识应用于万事万物的持续使命有关。如今,这一使命比以往任何时候都更加重要,它不仅要支持人类用户,还要支持快速增长的人工智能 "用户"--他们开始能够比人类更广泛、更深入地使用我们的技术。
Each new version of Wolfram Language represents a large amount of R&D by our team, and the encapsulation of a surprisingly large number of ideas about what should be implemented, and how it should be implemented. So, today, here it is: the latest stage in our four-decade journey to bring the superpower of the computational paradigm to everything.
Wolfram 语言的每一个新版本都代表着我们团队的大量研发工作,以及关于应该实现什么以及如何实现的大量想法。因此,今天,它来了:这是我们四十年来将计算范式的超级力量带入万事万物之旅的最新阶段。
There’s Now a Unified Wolfram App
现在有了统一的 Wolfram 应用程序
In the beginning we just had “Mathematica”—that we described as “A System for Doing Mathematics by Computer”. But the core of “Mathematica”—based on the very general concept of transformations for symbolic expressions—was always much broader than “mathematics”. And it didn’t take long before “mathematics” was an increasingly small part of the system we had built. We agonized for years about how to rebrand things to better reflect what the system had become. And eventually, just over a decade ago, we did the obvious thing, and named what we had “the Wolfram Language”.
一开始,我们只有"Mathematica"--我们将其描述为 "用计算机做数学的系统"。但 "Mathematica "的核心--基于符号表达式变换这一非常普遍的概念--始终比 "数学 "宽泛得多。没过多久,"数学 "在我们所构建的系统中所占的比重就越来越小。我们多年来一直在讨论如何重新命名,以更好地反映系统的现状。最终,就在十多年前,我们做了一件显而易见的事情,将我们拥有的东西命名为 "Wolfram 语言"。
But when it came to actual software products and executables, so many people were familiar with having a “Mathematica” icon on their desktop that we didn’t want to change that. Later we introduced Wolfram|One as a general product supporting Wolfram Language across desktop and cloud—with Wolfram Desktop being its desktop component. But, yes, it’s all been a bit confusing. Ultimately there’s just one “bag of bits” that implements the whole system we’ve built, even though there are different usage patterns, and differently named products that the system supports. Up to now, each of these different products has been a different executable, that’s separately downloaded.
但是,当涉及到实际软件产品和可执行文件时,很多人都熟悉在桌面上有一个 "Mathematica "图标,因此我们不想改变这一点。后来,我们推出了Wolfram|One,作为支持桌面和云的 Wolfram 语言的通用产品,Wolfram Desktop 就是其桌面组件。但是,是的,这一切都有点令人困惑。尽管有不同的使用模式以及该系统支持的不同名称的产品,但最终只有一个 "比特包 "来实现我们构建的整个系统。到目前为止,这些不同的产品都是不同的可执行文件,需要单独下载。
But starting with Version 14.1 we’re unifying all these things—so that now there’s just a single unified Wolfram app, that can be configured and activated in different ways corresponding to different products.
但从 14.1 版开始,我们将统一所有这些东西--现在只有一个统一的 Wolfram 应用程序,可以根据不同的产品以不同的方式进行配置和激活。
So now you just go to wolfram.com/download-center and download the Wolfram app:
现在,您只需访问 wolfram.com/download-center 并下载 Wolfram 应用程序:
![]()
After you’ve installed the app, you activate it as whatever product(s) you’ve got: Wolfram|One, Mathematica, Wolfram|Alpha Notebook Edition, etc. Why have separate products? Each one has a somewhat different usage pattern, and provides a somewhat different interface optimized for that usage pattern. But now the actual downloading of bits has been unified; you just have to download the unified Wolfram app and you’ll get what you need.
安装应用程序后,您可以将其激活为您所拥有的任何产品:Wolfram|One、Mathematica、Wolfram|Alpha 笔记本版等。为什么要有不同的产品?每个产品都有不同的使用模式,并提供了针对该使用模式进行优化的不同界面。但现在,实际的下载位已经统一;您只需下载统一的 Wolfram 应用程序,即可获得所需的内容。
Vector Databases and Semantic Search
矢量数据库和语义搜索
Let’s say you’ve got a million documents (or webpages, or images, or whatever) and you want to find the ones that are “closest” to something. Version 14.1 now has a function—SemanticSearch—for doing this. How does SemanticSearch work? Basically it uses machine learning methods to find “vectors” (i.e. lists) of numbers that somehow represent the “meaning” of each of your documents. Then when you want to know which documents are “closest” to something, SemanticSearch computes the vector for the something, and then sees which of the document vectors are closest to this vector.
比方说,您有一百万个文档(或网页、图片或其他),而您想找出与某些内容 "最接近 "的文档。14.1 版现在有了一个函数-- SemanticSearch ,可以实现这一功能。 SemanticSearch 是如何工作的呢?基本上,它使用机器学习方法来查找数字 "向量"(即列表),这些数字以某种方式代表了每个文档的 "含义"。然后,当您想知道哪些文档 "最接近 "某项内容时, SemanticSearch 会计算该内容的向量,然后查看哪些文档向量最接近该向量。
In principle one could use Nearest to find closest vectors. And indeed this works just fine for small examples where one can readily store all the vectors in memory. But SemanticSearch uses a full industrial-strength approach based on the new vector database capabilities of Version 14.1—which can work with huge collections of vectors stored in external files.
原则上,我们可以使用 Nearest 来查找最接近的向量。对于可以随时将所有向量存储在内存中的小型示例,这种方法确实非常有效。但是, SemanticSearch 使用的是基于 14.1 版新向量数据库功能的完全工业级方法,它可以处理存储在外部文件中的大量向量集合。
There are lots of ways to use both SemanticSearch and vector databases. You can use them to find documents, snippets within documents, images, sounds or anything else whose “meaning” can somehow be captured by a vector of numbers. Sometimes the point is to retrieve content directly for human consumption. But a particularly strong modern use case is to set up “retrieval-augmented generation” (RAG) for LLMs—in which relevant content found with a vector database is used to provide a “dynamic prompt” for the LLM. And indeed in Version 14.1—as we’ll discuss later—we now have LLMPromptGenerator to implement exactly this pipeline.
使用 SemanticSearch 和矢量数据库的方法有很多。您可以使用它们查找文件、文件中的片段、图像、声音或其他任何其 "含义 "可以通过数字矢量捕获的内容。有时,重点是直接检索供人类消费的内容。但是,一个特别强大的现代用例是为LLMs设置 "检索增强生成"(RAG),即使用矢量数据库找到的相关内容为LLM提供 "动态提示"。事实上,在 14.1 版中--我们稍后将讨论--我们现在有了 LLMPromptGenerator 来实现这一流水线。
But let’s come back to SemanticSearch on its own. Its basic design is modeled after TextSearch, which does keyword-based searching of text. (Note, though, that SemanticSearch also works on many things other than text.)
不过,让我们回到 SemanticSearch 本身。它的基本设计仿效了 TextSearch ,后者可以对文本进行基于关键字的搜索。(但请注意, SemanticSearch 也适用于文本以外的许多内容)。
In direct analogy to CreateSearchIndex for TextSearch, there’s now a CreateSemanticSearchIndex for SemanticSearch. Let’s do a tiny example to see how it works. Essentially we’re going to make an (extremely restricted) “inverse dictionary”. We set up a list of definition ![]() word elements:
word elements:
与 TextSearch 的 CreateSearchIndex 直接类比,现在 SemanticSearch 也有了 CreateSemanticSearchIndex 。让我们举个小例子来看看它是如何工作的。从根本上说,我们要创建一个(极其有限的)"反向字典"。我们建立了一个定义 ![]() 词元素的列表:
词元素的列表:

Now create a semantic search index from this:
现在从中创建一个语义搜索索引:

Behind the scenes this is a vector database. But we can access it with SemanticSearch:
在幕后,这是一个矢量数据库。但我们可以使用 SemanticSearch 访问它:
And since “whale” is considered closest, it comes first.
由于 "鲸鱼 "被认为是最接近的,所以它排在第一位。
What about a more realistic example? Instead of just using 3 words, let’s set up definitions for all words in the dictionary. It takes a little while (like a few minutes) to do the machine learning feature extraction for all the definitions. But in the end you get a new semantic search index:
举个更现实的例子怎么样?我们不要只用 3 个词,而是为字典中的所有词建立定义。对所有定义进行机器学习特征提取需要一点时间(比如几分钟)。但最终你会得到一个新的语义搜索索引:

This time it has 39,186 entries—but SemanticSearch picks out the (by default) 10 that it considers closest to what you asked for (and, yes, there’s an archaic definition of “seahorse” as “walrus”):
这次有 39,186 个条目,但 SemanticSearch 挑选出了(默认情况下)它认为最接近您要求的 10 个条目(是的,"海马 "的古老定义是 "海象"):
We can see a bit more detail about what’s going on by asking SemanticSearch to explicitly show us distances:
通过要求 SemanticSearch 明确显示距离,我们可以看到更多细节:

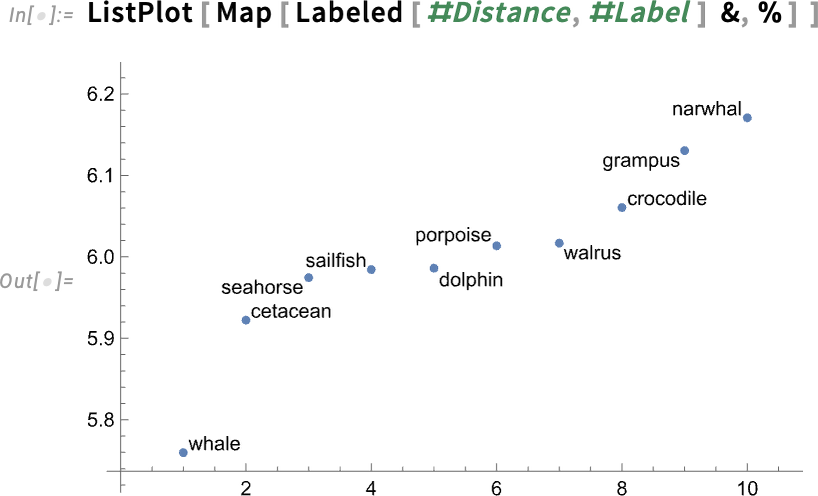
And plotting these we can see that “whale” is the winner by a decent margin:
通过绘制这些图表,我们可以看到 "鲸鱼 "以相当大的优势胜出:
One subtlety when dealing with semantic search indices is where to store them. When they’re sufficiently small, you can store them directly in memory, or in a notebook. But usually you’ll want to store them in a separate file, and if you want to share an index you’ll want to put this file in the cloud. You can do this either interactively from within a notebook
处理语义搜索索引的一个微妙之处在于如何存储它们。当索引足够小的时候,可以直接存储在内存或笔记本中。但通常情况下,你会想把它们存储在一个单独的文件中,如果你想共享索引,你会想把这个文件放到云中。您可以在笔记本中以交互方式完成此操作

or programmatically: 或编程:
And now the SemanticSearchIndex object you have can be used by anyone, with its data being accessed in the cloud.
现在,任何人都可以使用您拥有的 SemanticSearchIndex 对象,并通过云访问其数据。
In most cases SemanticSearch will be what you need. But sometimes it’s worthwhile to “go underneath” and directly work with vector databases. Here’s a collection of small vectors:
在大多数情况下, SemanticSearch 可以满足您的需要。但有时值得 "深入",直接使用矢量数据库。下面是一组小型矢量:

We can use Nearest to find the nearest vector to one we give:
我们可以使用 Nearest 来找到与我们给出的向量最接近的向量:
But we can also do this with a vector database. First we create the database:
不过,我们也可以使用矢量数据库来实现这一功能。首先,我们创建数据库:

And now we can search for the nearest vector to the one we give:
现在,我们可以寻找与我们给出的向量最接近的向量:
In this case we get exactly the same answer as from Nearest. But whereas the mission of Nearest is to give us the mathematically precise nearest vector, VectorDatabaseSearch is doing something less precise—but is able to do it for extremely large numbers of vectors that don’t need to be stored directly in memory.
在这种情况下,我们得到的答案与 Nearest 完全相同。但是, Nearest 的任务是为我们提供数学上最精确的向量,而 VectorDatabaseSearch 所做的事情却不那么精确--但却能为不需要直接存储在内存中的大量向量提供精确度。
Those vectors can come from anywhere. For example, here they’re coming from extracting features from some images:
这些向量可以来自任何地方。例如,这里的矢量来自从一些图像中提取的特征:

Now let’s say we’ve got a specific image. Then we can search our vector database to get the image whose feature vector is closest to the one for the image we provided:
现在,假设我们得到了一张特定的图像。那么我们就可以搜索我们的向量数据库,找到与我们提供的图像特征向量最接近的图像:

And, yes, this works for other kinds of objects too:
是的,这也适用于其他类型的物体:

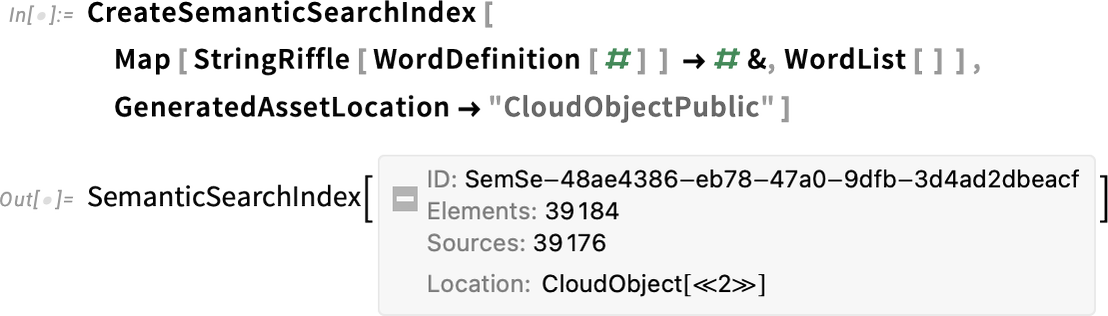
CreateSemanticSearchIndex and CreateVectorDatabase create vector databases from scratch using data you provide. But—just like with text search indices—an important feature of vector databases is that you can incrementally add to them. So, for example, UpdateSemanticSearchIndex and AddToVectorDatabase let you efficiently add individual entries or lists of entries to vector databases.
CreateSemanticSearchIndex 和 CreateVectorDatabase 使用您提供的数据从头开始创建矢量数据库。但是,就像文本搜索索引一样,矢量数据库的一个重要特点是可以逐步添加。因此,举例来说, UpdateSemanticSearchIndex 和 AddToVectorDatabase 可以让你有效地向矢量数据库添加单个条目或条目列表。
In addition to providing capabilities for building (and growing) your own vector databases, there are several pre-built vector databases that are now available in the Wolfram Data Repository:
除了提供用于构建(和扩展)您自己的矢量数据库的功能外,Wolfram 数据库中还有几个预构建的矢量数据库:

So now we can use a pre-built vector database of Wolfram Language function documentation to do a semantic search for snippets that are “semantically close” to being about iterating functions:
因此,我们现在可以使用 Wolfram 语言函数文档的预建向量数据库,对 "语义上接近 "迭代函数的片段进行语义搜索:

(In the next section, we’ll see how to actually “synthesize a report” based on this.)
(在下一节中,我们将了解如何在此基础上实际 "合成一份报告")。
The basic function of SemanticSearch is to determine what “chunks of content” are closest to what you are asking about. But given a semantic search index (AKA vector database) there are also other important things you can do. One of them is to use TextSummarize to ask not for specific chunks but rather for some kind of overall summary of what can be said about a given topic from the content in the semantic search index:
SemanticSearch 的基本功能是确定哪些 "内容块 "最接近您所询问的内容。但是,考虑到语义搜索索引(又称矢量数据库),您还可以做其他一些重要的事情。其中之一就是使用 TextSummarize 不是询问具体的内容块,而是询问从语义搜索索引中的内容中可以对给定主题说什么的某种总体总结:

RAGs and Dynamic Prompting for LLMs
LLMs 的 RAG 和动态提示
How does one tell an LLM what one wants it to do? Fundamentally, one provides a prompt, and then the LLM generates output that “continues” that prompt. Typically the last part of the prompt is the specific question (or whatever) that a user is asking. But before that, there’ll be “pre-prompts” that prime the LLM in various ways to determine how it should respond.
如何告诉 LLM 要做什么?从根本上说,用户需要提供一个提示,然后 LLM 会生成 "继续 "该提示的输出。通常,提示的最后一部分是用户提出的具体问题(或其他)。但在此之前,会有一些 "预提示 "以各种方式为 LLM 提供启动条件,以确定它应该如何响应。
In Version 13.3 in mid-2023 (i.e. a long time ago in the world of LLMs!) we introduced LLMPrompt as a symbolic way to specify a prompt, and we launched the Wolfram Prompt Repository as a broad source for pre-built prompts. Here’s an example of using LLMPrompt with a prompt from the Wolfram Prompt Repository:
在 2023 年中期的 13.3 版本中(即 LLMs 世界中的很久以前!),我们引入了 LLMPrompt 作为指定提示符的符号方式,并推出了 Wolfram 提示符库,作为预建提示符的广泛来源。下面是使用 LLMPrompt 和 Wolfram 提示库中的提示的示例:
In its simplest form, LLMPrompt just adds fixed text to “pre-prompt” the LLM. LLMPrompt is also set up to take arguments that modify the text it’s adding:
在其最简单的形式中, LLMPrompt 只是添加固定文本,以 "预先提示"LLM。此外, LLMPrompt 还可以接受参数来修改所添加的文本:
But what if one wants the LLM to be pre-prompted in a way that depends on information that’s only available once the user actually asks their question (like, for example, the text of the question itself)? In Version 14.1 we’re adding LLMPromptGenerator to dynamically generate pre-prompts. And it turns out that this kind of “dynamic prompting” is remarkably powerful, and—particularly together with tool calling—opens up a whole new level of capabilities for LLMs.
但是,如果希望 LLM 的预提示方式取决于用户实际提问时才能获得的信息(例如,问题本身的文本),该怎么办?在 14.1 版中,我们将添加 LLMPromptGenerator 以动态生成预提示。事实证明,这种 "动态提示 "非常强大,尤其是与工具调用相结合,为 LLMs 开启了一个全新的功能层次。
For example, we can set up a prompt generator that produces a pre-prompt that gives the registered name of the user, so the LLM can use this information when generating its answer:
例如,我们可以设置一个提示生成器,生成一个提供用户注册名称的预提示,这样 LLM 就可以在生成答案时使用这些信息:

Or for example here the prompt generator is producing a pre-prompt about sunrise, sunset and the current time:
例如,提示生成器正在生成有关日出、日落和当前时间的预提示:

And, yes, if the pre-prompt contains extra information (like about the Moon) the LLM will (probably) ignore it:
是的,如果预提示包含额外信息(如关于月球的信息),LLM(很可能)会忽略它:

As another example, we can take whatever the user asks, and first do a web search on it, then include as a pre-prompt snippets we get from the web. The result is that we can get answers from the LLM that rely on specific “web knowledge” that we can’t expect will be “known in detail” by the raw LLM:
再举个例子,无论用户问什么,我们都可以首先对其进行网络搜索,然后将从网络中获取的片段作为预提示。这样做的结果是,我们可以从 LLM 中获得依赖于特定 "网络知识 "的答案,而我们无法期望原始 LLM 会 "详细了解 "这些知识:

But often one doesn’t want to just “search at random on the web”; instead one wants to systematically retrieve information from some known source to give as “briefing material” to the LLM to help it in generating its answer. And a typical way to implement this kind of “retrieval-augmented generation (RAG)” is to set up an LLMPromptGenerator that uses the SemanticSearch and vector database capabilities that we introduced in Version 14.1.
但是,我们通常并不希望只是 "在网上随意搜索";相反,我们希望从某些已知来源系统地检索信息,作为 "简要材料 "提供给 LLM 以帮助它生成答案。实现这种 "检索增强生成 (RAG) "的典型方法是建立一个 LLMPromptGenerator ,使用我们在 14.1 版中介绍的 SemanticSearch 和矢量数据库功能。
So, for example, here’s a semantic search index generated from my (rather voluminous) writings:
因此,举例来说,这里有一个从我的著作(相当多)中生成的语义搜索索引:

By setting up a prompt generator based on this, I can now ask the LLM “personal questions”:
在此基础上设置一个提示生成器,现在我就可以提出 LLM "个人问题 "了:
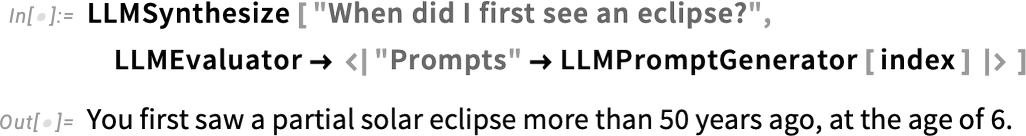
How did the LLM “know that”? Internally the prompt generator used SemanticSearch to generate a collection of snippets, which the LLM then “trawled through” to produce a specific answer:
LLM 是如何 "知道 "这一点的呢?在内部,提示生成器使用 SemanticSearch 生成一系列片段,然后 LLM 对这些片段进行 "搜索",以生成特定的答案:

It’s already often very useful just to “retrieve static text” to “brief” the LLM. But even more powerful is to brief the LLM with what it needs to call tools that can do further computation, etc. So, for example, if you want the LLM to write and run Wolfram Language code that uses functions you’ve created, you can do that by having it first “read the documentation” for those functions.
仅仅 "检索静态文本 "来 "简要介绍"LLM就已经非常有用了。但更强大的是,向 LLM 简要介绍它需要调用哪些工具来进行进一步计算等。因此,举例来说,如果您希望 LLM 使用您创建的函数来编写和运行 Wolfram 语言代码,您可以让它首先 "阅读 "这些函数的 "文档"。
As an example, this uses a prompt generator that uses a semantic search index built from the Wolfram Function Repository:
举例来说,提示生成器使用从 Wolfram 函数库建立的语义搜索索引:

Connect to Your Favorite LLM
连接到您喜爱的 LLM
There are now many ways to use LLM functionality from within the Wolfram Language, and Wolfram Notebooks. You can do it programmatically, with LLMFunction, LLMSynthesize, etc. You can do it interactively through Chat Notebooks and related chat capabilities.
现在有很多方法可以在 Wolfram 语言和 Wolfram 笔记本中使用 LLM 功能。您可以通过 LLMFunction 、 LLMSynthesize 等程序来实现。您可以通过 Chat Notebooks 和相关聊天功能进行交互。
But (at least for now) there’s no full-function LLM built directly into the Wolfram Language. So that means that (at least for now) you have to choose your “flavor” of external LLM to power Wolfram Language LLM functionality. And in Version 14.1 we have support for basically all major available foundation-model LLMs.
但是(至少目前)Wolfram 语言中还没有直接内置全功能 LLM 的功能。因此,这意味着(至少现在)您必须选择 "适合您的 "外部 LLM 来支持 Wolfram 语言 LLM 功能。在 14.1 版中,我们基本上支持所有主要的可用基础模型 LLMs。
We’ve made it as straightforward as possible to set up connections to external LLMs. Once you’ve done it, you can select what you want directly in any Chat Notebook
我们尽可能简化了与外部 LLMs 的连接设置。完成后,您可以直接在任何聊天笔记本中选择您想要的内容

or from your global Preferences:
或从全局 Preferences 中调用:

When you’re using a function you specify the “model” (i.e. service and specific model name) as part of the setting for LLMEvaluator:
使用函数时,您需要指定 "模型"(即服务和特定模型名称),作为 LLMEvaluator 设置的一部分:

In general you can use LLMConfiguration to define the whole configuration of an LLM you want to connect to, and you can make a particular configuration your default either interactively using Preferences, or by explicitly setting the value of $LLMEvaluator.
一般来说,您可以使用 LLMConfiguration 来定义您要连接的 LLM 的整个配置,您可以使用 Preferences 以交互方式或通过显式设置 $LLMEvaluator 的值将特定配置设为默认配置。
So how do you initially set up a connection to a new LLM? You can do it interactively by pressing Connect in the AI Settings pane of Preferences. Or you can do it programmatically using ServiceConnect:
那么,如何初始化与新的 LLM 的连接呢?您可以通过在 Preferences 的 AI Settings 窗格中按下 Connect 来交互完成。或者,您也可以使用 ServiceConnect 以编程的方式进行操作:

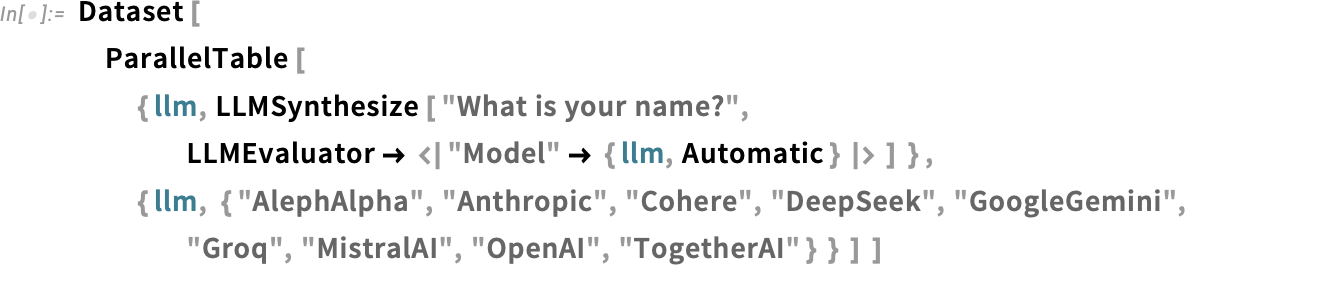
At the “ServiceConnect level” you have very direct access to the features of LLM APIs, though unless you’re studying LLM APIs you probably won’t need to use these. But talking of LLM APIs, one of the things that’s now easy to do with Wolfram Language is to compare LLMs, for example programmatically sending the same question to multiple LLMs:
在" ServiceConnect 级",您可以非常直接地访问 LLM API 的功能,不过除非您正在学习 LLM API,否则您可能不需要使用这些功能。不过,说到 LLM API,Wolfram 语言现在可以轻松完成的一件事就是比较 LLMs ,例如以编程方式将同一个问题发送到多个 LLMs 中:
And in fact we’ve recently started posting weekly results that we get from a full range of LLMs on the task of writing Wolfram Language code (conveniently, the exercises in my book An Elementary Introduction to the Wolfram Language have textual “prompts”, and we have a well-developed system that we’ve used for many years in assessing code for the online course based on the book):
事实上,我们最近已经开始发布每周LLMs关于编写 Wolfram 语言代码任务的各种结果(很方便、我的书An Elementary Introduction to the Wolfram Language中的练习都有文字 "提示",而且我们有一套完善的系统,多年来一直用于评估基于该书的在线课程的代码):
Symbolic Arrays and Their Calculus
符号数组及其微积分
I want A to be an n×n matrix. I don’t want to say what its elements are, and I don’t even want to say what n is. I just want to have a way to treat the whole thing symbolically. Well, in Version 14.1 we’ve introduced MatrixSymbol to do that.
我希望 A 是一个 n×n 矩阵。我不想说它的元素是什么,甚至不想说 n 是什么。我只想有一种方法来符号化地处理整件事情。在 14.1 版中,我们引入了 MatrixSymbol 来做到这一点。
A MatrixSymbol has a name (just like an ordinary symbol)—and it has a way to specify its dimensions. We can use it, for example, to set up a symbolic representation for our matrix A:
MatrixSymbol 有一个名称(就像普通符号一样),并且可以指定其尺寸。例如,我们可以用它为矩阵 A 设置符号表示:
Hovering over this in a notebook, we’ll get a tooltip that explains what it is:
在笔记本中将鼠标悬停在这一点上,我们会得到一个工具提示,说明这是什么:

We can ask for its dimensions as a tensor:
我们可以以张量的形式求出它的维数:
Here’s its inverse, again represented symbolically:
下面是它的倒数,同样用符号表示:
That also has dimensions n×n:
它的尺寸也是 n×n :
In Version 14.1 you can not only have symbolic matrices, you can also have symbolic vectors and, for that matter, symbolic arrays of any rank. Here’s a length-n symbolic vector (and, yes, we can have a symbolic vector named v that we assign to a symbol v):
在 14.1 版中,您不仅可以使用符号矩阵,还可以使用符号向量,以及任意秩的符号数组。下面是一个长度为n 的符号向量(是的,我们可以拥有一个名为 v 的符号向量,并将其赋值给符号 v ):
So now we can construct something like the quadratic form:
因此,现在我们可以构建类似二次方程的形式:
A classic thing to compute from this is its gradient with respect to the vector ![]() :
:
由此计算出的一个经典结果是它相对于向量 ![]() 的梯度:
的梯度:
And actually this is just the same as the “vector derivative”:
实际上,这与 "矢量导数 "是一样的:
If we do a second derivative we get:
如果进行二阶导数运算,我们可以得到
What happens if we differentiate ![]() with respect to
with respect to ![]() ? Well, then we get a symbolic identity matrix
? Well, then we get a symbolic identity matrix
如果我们将 ![]() 与
与 ![]() 进行微分,会发生什么情况呢?那么,我们会得到一个符号标识矩阵
进行微分,会发生什么情况呢?那么,我们会得到一个符号标识矩阵
which again has dimensions n×n:
其尺寸也是 n×n :
![]() is a rank-2 example of a symbolic identity array:
is a rank-2 example of a symbolic identity array:
![]() 是符号标识数组的秩 2 示例:
是符号标识数组的秩 2 示例:
If we give n an explicit value, we can get an explicit componentwise array:
如果我们给 n 一个显式值,就能得到一个显式分量数组:
Let’s say we have a function of ![]() , like Total. Once again we can find the derivative with respect to
, like Total. Once again we can find the derivative with respect to ![]() :
:
假设我们有一个 ![]() 的函数,比如 Total 。我们可以再次求出关于
的函数,比如 Total 。我们可以再次求出关于 ![]() 的导数:
的导数:
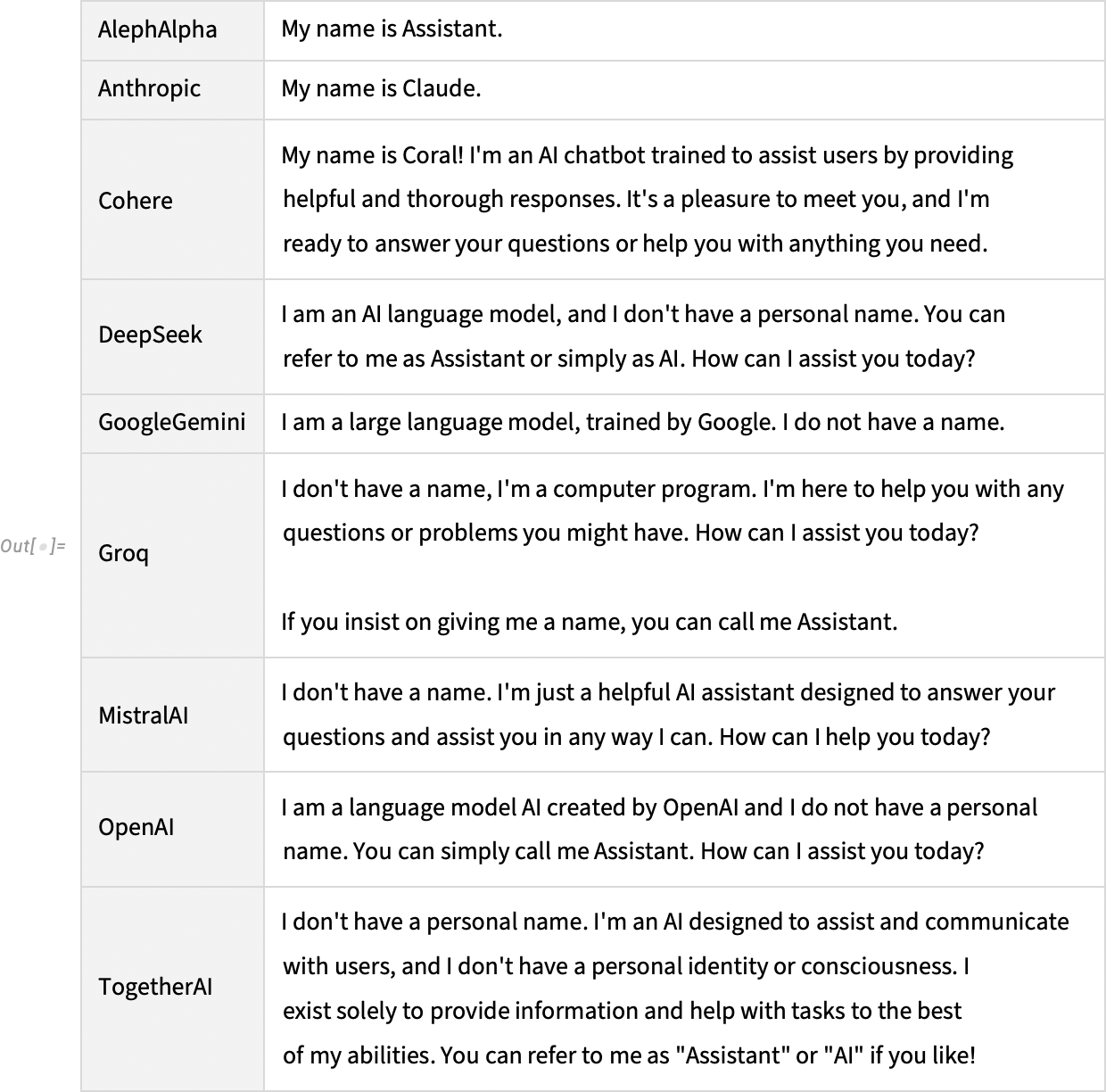
And now we see another symbolic array construct: SymbolicOnesArray:
现在,我们看到了另一种符号数组结构: SymbolicOnesArray :
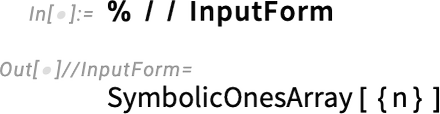
This is simply an array whose elements are all 1:
这只是一个元素全为 1 的数组:
Differentiating a second time gives us a SymbolicZerosArray:
进行第二次微分后,我们得到了 SymbolicZerosArray :
Although we’re not defining explicit elements for ![]() , it’s sometimes important to specify, for example, that all the elements are reals:
, it’s sometimes important to specify, for example, that all the elements are reals:
虽然我们没有为 ![]() 定义明确的元素,但有时指定所有元素都是实数也很重要:
定义明确的元素,但有时指定所有元素都是实数也很重要:
For a vector whose elements are reals, it’s straightforward to find the derivative of the norm:
对于元素为实数的矢量,可以直接求出准则的导数:
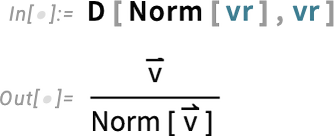
The third derivative, though, is a bit more complicated:
不过,第三次导数就比较复杂了:
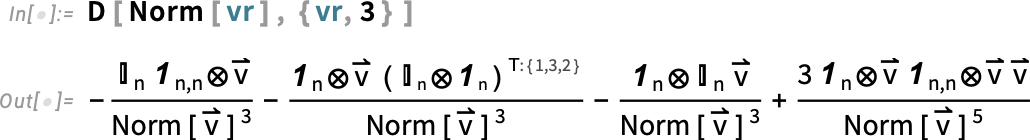
The ⊗ here is TensorProduct, and the T:(1,3,2) represents Transpose[..., {1, 3, 2}].
这里的⊗表示 TensorProduct ,T:(1,3,2) 表示 Transpose [..., {1, 3, 2}] 。
In the Wolfram Language, a symbol, say s, can stand on its own, and represent a “variable”. It can also appear as a head—as in s[x]—and represent a function. And the same is true for vector and matrix symbols:
在 Wolfram 语言中,一个符号,例如 s 可以独立存在,代表一个 "变量"。它也可以作为头部出现--如 s[x] 并代表一个函数。向量和矩阵符号也是如此:
Importantly, the chain rule also works for matrix and vector functions:
重要的是,链式法则也适用于矩阵和矢量函数:
Things get a bit trickier when one’s dealing with functions of matrices:
在处理矩阵的函数时,情况就变得有点棘手了:

The ![]() here represents ArrayDot[..., ..., 2], which is a generalization of Dot. Given two arrays u and v, Dot will contract the last index of u with the first index of v:
here represents ArrayDot[..., ..., 2], which is a generalization of Dot. Given two arrays u and v, Dot will contract the last index of u with the first index of v:
这里的 ![]() 表示 ArrayDot [..., ..., 2] ,它是 Dot 的概括。如果给定两个数组 u 和 v , Dot 将用 v 的第一个索引收缩 u 的最后一个索引:
表示 ArrayDot [..., ..., 2] ,它是 Dot 的概括。如果给定两个数组 u 和 v , Dot 将用 v 的第一个索引收缩 u 的最后一个索引:
ArrayDot[u, v, n], on the other hand, contracts the last n indices of u with the first n of v.
ArrayDot [u, v, n] 则是将 n 的最后一个 u 索引与 n 的第一个 v 索引合并。
But now in this particular example all the indices get “contracted out”:
但在这个例子中,所有指数都被 "外包 "了:
We’ve talked about symbolic vectors and matrices. But—needless to say—what we have is completely general, and will work for arrays of any rank. Here’s an example of a p×q×r array:
我们已经讨论过符号向量和矩阵。但不用说,我们所掌握的完全是通用方法,适用于任何秩的数组。下面是一个 p×q×r 数组的示例:

The overscript ![]() indicates that this is an array of rank 3.
indicates that this is an array of rank 3.
上标 ![]() 表明这是一个秩为 3 的数组。
表明这是一个秩为 3 的数组。
When one takes derivatives, it’s very easy to end up with high-rank arrays. Here’s the result of differentiating with respect to a matrix:
求导时,很容易得到高阶数组。下面是对矩阵进行微分的结果:
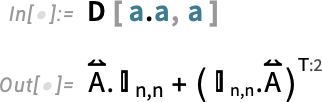
![]() is a rank-4 n×n×n×n identity array.
is a rank-4 n×n×n×n identity array.
![]() 是一个秩 4 n×n×n×n 身份数组。
是一个秩 4 n×n×n×n 身份数组。
When one’s dealing with higher-rank objects, there’s one more construct that appears—that we call SymbolicDeltaProductArray. Let’s set up a rank-3 array with dimensions 3×3×3:
在处理高阶对象时,还会出现一个结构,我们称之为 SymbolicDeltaProductArray 。让我们建立一个尺寸为 3×3×3 的秩 3 数组:

Now let’s compute a derivative:
现在我们来计算导数:
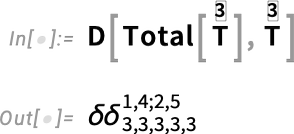
The result is a rank-5 array that’s effectively a combination of two KroneckerDelta objects for indices 1,4 and 2,5, respectively:
结果是一个秩 5 数组,它实际上是两个 KroneckerDelta 对象的组合,分别位于索引 1,4 和 2,5 处:
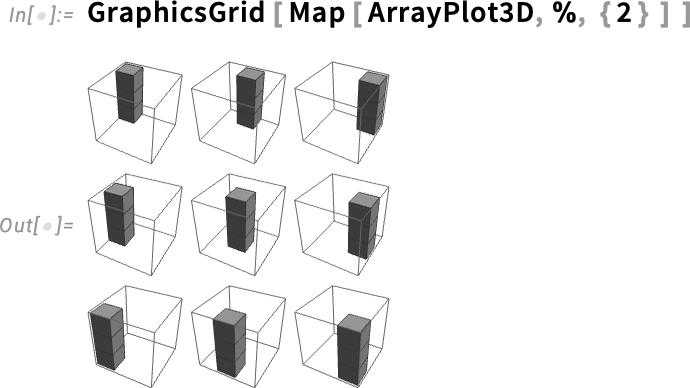
We can visualize this with ArrayPlot3D:
我们可以用 ArrayPlot3D 将其形象化:
The most common way to deal with arrays in the Wolfram Language has always been in terms of explicit lists of elements. And in this representation it’s extremely convenient that operations are normally done elementwise:
在 Wolfram 语言中,处理数组的最常见方式一直是使用元素的显式列表。在这种表示法中,操作通常是按元素进行的,非常方便:
Non-lists are then by default treated as scalars—and for example here added into every element:
因此,非列表默认被视为标量,例如在这里被添加到每个元素中:
But now there’s something new, namely symbolic arrays—which in effect implicitly contain multiple list elements, and thus can’t be “added into every element”:
但现在有了新东西,那就是符号数组--它实际上隐含了多个列表元素,因此不能 "添加到每个元素中":
This is what happens when we have an “ordinary scalar” together with a symbolic vector:
这就是将 "普通标量 "与符号向量结合在一起的结果:
How does this work? “Under the hood” there’s a new attribute NonThreadable which specifies that certain heads (like ArraySymbol) shouldn’t be threaded by Listable functions (like Plus).
这是如何实现的?在 "引擎盖 "下有一个新属性 NonThreadable ,它指定某些头(如 ArraySymbol )不应被 Listable 函数(如 Plus )线程化。
By the way, ever since Version 9 a dozen years ago we’ve had a limited mechanism for assuming that symbols represent vectors, matrices or arrays—and now that mechanism interoperates with all our new symbolic array functionality:
顺便提一下,自从十几年前Version 9开始,我们就有了一种有限的机制来假定符号代表向量、矩阵或数组,现在这种机制已经与我们所有新的符号数组功能实现了互操作:
When you’re doing explicit computations there’s often no choice but to deal directly with individual array elements. But it turns out that there are all sorts of situations where it’s possible to work instead in terms of “whole” vectors, matrices, etc. And indeed in the literature of fields like machine learning, optimization, statistics and control theory, it’s become quite routine to write down formulas in terms of symbolic vectors, matrices, etc. And what Version 14.1 now adds is a streamlined way to compute in terms of these symbolic array constructs.
在进行显式计算时,通常别无选择,只能直接处理单个数组元素。但事实证明,在各种情况下,都可以用 "整体 "向量、矩阵等来代替。事实上,在机器学习、优化、统计和控制理论等领域的文献中,用符号向量、矩阵等来书写公式已经成为一种惯例。现在,14.1 版增加了一种简化的方法,可以用这些符号数组结构进行计算。
The results are often very elegant. So, for example, here’s how one might set up a general linear least-squares problem using our new symbolic array constructs. First we define a symbolic n×m matrix A, and symbolic vectors b and x:
结果往往非常优雅。因此,举例来说,我们可以使用新的符号数组结构来设置一般的线性最小二乘法问题。首先,我们定义一个符号 n×m 矩阵 A,以及符号向量 b 和 x :

Our goal is to find a vector ![]() that minimizes
that minimizes ![]() . And with our definitions we can now immediately write down this quantity:
. And with our definitions we can now immediately write down this quantity:
我们的目标是找到一个使 ![]() 最小化的向量
最小化的向量 ![]() 。有了定义,我们现在就可以立即写出这个量:
。有了定义,我们现在就可以立即写出这个量:

To extremize it, we compute its derivative
为了使其极端化,我们计算它的导数

and to ensure we get a minimum, we compute the second derivative:
为确保得到最小值,我们计算二阶导数:

These are standard textbook formulas, but the cool thing is that in Version 14.1 we’re now in a position to generate them completely automatically. By the way, if we take another derivative, the result will be a zero tensor:
这些都是标准的教科书公式,但最酷的是,在 14.1 版中,我们现在可以完全自动生成这些公式。顺便说一句,如果我们再取一个导数,结果将是一个零张量:

We can look at other norms too:
我们还可以看看其他规范:


Binomials and Pitchforks: Navigating Mathematical Conventions
二项式与锄头:数学常规导航
Binomial coefficients have been around for at least a thousand years, and one might not have thought there could possibly be anything shocking or controversial about them anymore (notwithstanding the fictional Treatise on the Binomial Theorem by Sherlock Holmes’s nemesis Professor Moriarty). But in fact we have recently been mired in an intense debate about binomial coefficients—which has caused us in Version 14.1 to introduce a new function PascalBinomial alongside our existing Binomial.
二项式系数已经存在了至少一千年,人们可能不会再认为它有什么令人震惊或有争议的地方(尽管福尔摩斯的克星莫里亚蒂教授虚构了Treatise on the Binomial Theorem )。但事实上,我们最近陷入了关于二项式系数的激烈争论,这使得我们在 14.1 版中除了现有的 Binomial 之外,还引入了一个新函数 PascalBinomial 。
When one’s dealing with positive integer arguments, there’s no issue with binomials. And even when one extends to generic complex arguments, there’s again a unique way to do this. But negative integer arguments are a special degenerate case. And that’s where there’s trouble—because there are two different definitions that have historically been used.
在处理正整数参数时,不存在二项式的问题。即使扩展到一般的复数参数,也有独特的方法。但负整数参数是一种特殊的退化情况。这就是问题所在--因为历史上有两种不同的定义。
In early versions of Mathematica, we picked one of these definitions. But over time we realized that it led to some subtle inconsistencies, and so for Version 7—in 2008—we changed to the other definition. Some of our users were happy with the change, but some were definitely not. A notable (vociferous) example was my friend Don Knuth, who has written several well-known books that make use of binomial coefficients—always choosing what amounts to our pre-2008 definition.
在 Mathematica 的早期版本中,我们选择了其中一个定义。但随着时间的推移,我们意识到这会导致一些微妙的不一致,因此在 2008 年第 7 版中,我们改用了另一种定义。我们的一些用户对这一改变很满意,但也有一些用户绝对不满意。我的朋友Don Knuth就是一个明显的(大声疾呼的)例子。
So what could we do about this? For a while we thought about adding an option to Binomial, but to do this would have broken our normal conventions for mathematical functions. And somehow we kept on thinking that there was ultimately a “right answer” to how binomial coefficients should be defined. But after a lot of discussion—and historical research—we finally concluded that since at least before 1950 there have just been two possible definitions, each with their own advantages and disadvantages, with no obvious “winner”. And so in Version 14.1 we decided just to introduce a new function PascalBinomial to cover the “other definition”.
那么我们能做些什么呢?有一段时间,我们曾考虑为 Binomial 添加一个选项,但这样做会破坏我们对数学函数的正常约定。而且不知何故,我们一直认为二项式系数的定义最终会有一个 "正确答案"。但经过大量讨论和历史研究,我们最终得出结论,至少从 1950 年以前开始,就一直存在两种可能的定义,各有利弊,没有明显的 "胜者"。因此,在 14.1 版中,我们决定引入一个新函数 PascalBinomial 来涵盖 "其他定义"。
And—though at first it might not seem like much—here’s a big difference between Binomial and PascalBinomial:
而且--虽然初看起来可能没什么-- Binomial 和 PascalBinomial 之间有很大的区别:
Part of why things get complicated is the relation to symbolic computation. Binomial has a symbolic simplification rule, valid for any n:
事情变得复杂的部分原因在于与符号计算的关系。 Binomial 有一个符号简化规则,对任何 n 都有效:
But there isn’t a corresponding generic simplification rule for PascalBinomial:
但是, PascalBinomial 并没有相应的通用简化规则:
FunctionExpand shows us the more nuanced result in this case:
FunctionExpand 向我们展示了这种情况下更细微的结果:

To see a bit more of what’s going on, we can compute arrays of nonzero results for Binomial and PascalBinomial:
为了进一步了解情况,我们可以计算 Binomial 和 PascalBinomial 的非零结果数组:
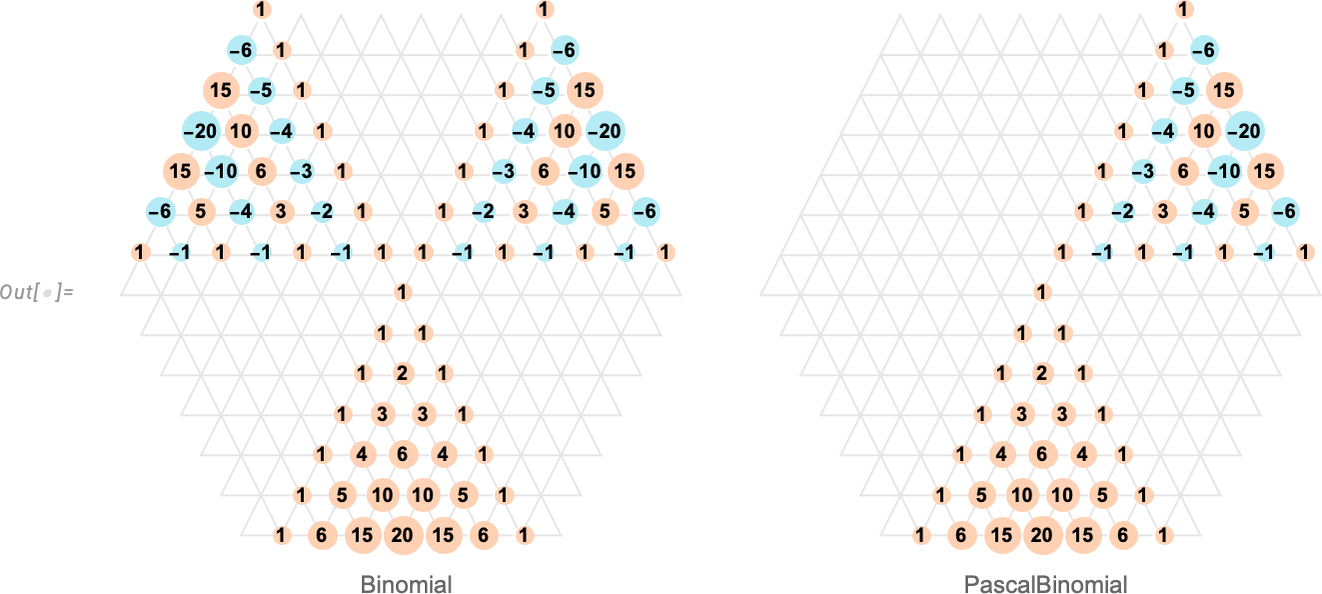
Binomial[n, k] has the “nice feature” that it’s symmetric in k even when n < 0. But this has the “bad consequence” that Pascal’s identity (that says a particular binomial coefficient is the sum of two coefficients “above it”) isn’t always true. PascalBinomial, on the other hand, always satisfies the identity, and it’s in recognition of this that we put “Pascal” in its name.
Binomial [n, k] 有一个 "好特点",那就是即使 n < 0,它在 k 中也是对称的。但这有一个 "坏结果",那就是 帕斯卡特性(即一个特定的二项式系数是 "在它上面 "的两个系数之和)并不总是正确的。另一方面, PascalBinomial 总是满足同一性,正是认识到这一点,我们才把 "帕斯卡 "放在它的名字中。
And, yes, this is all quite subtle. And, remember, the differences between Binomial and PascalBinomial only show up at negative integer values. Away from such values, they’re both given by the same expression, involving gamma functions. But at negative integer values, they correspond to different limits, respectively:
是的,这一切都很微妙。请记住, Binomial 和 PascalBinomial 之间的差异只在负整数值时才会显现。在负整数值之外,它们的表达式相同,都涉及伽马函数。但在负整数值时,它们分别对应不同的极限:
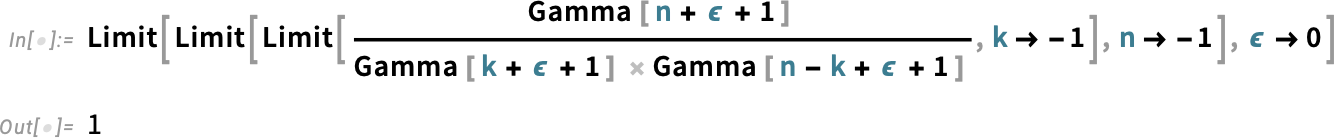
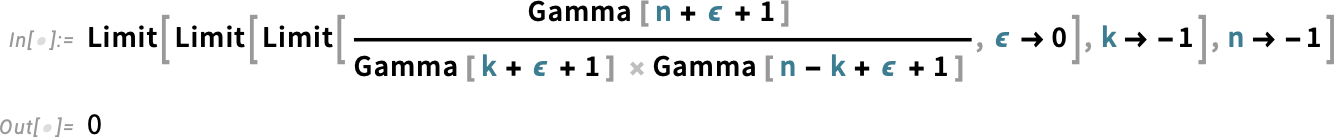
The story of Binomial and PascalBinomial is a complicated one that mainly affects only the upper reaches of discrete mathematics. But there’s another, much more elementary convention that we’ve also tackled in Version 14.1: the convention of what the arguments of trigonometric functions mean.
Binomial 和 PascalBinomial 是一个复杂的故事,主要影响离散数学的上游。不过,我们在 14.1 版中还处理了另一个更基本的约定:三角函数参数含义的约定。
We’ve always taken the “fundamentally mathematical” point of view that the x in Sin[x] is in radians:
我们一直从 "基本数学 "的角度出发,认为 Sin [x] 中的x 是以弧度为单位的:
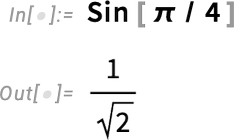
You’ve always been able to explicitly give the argument in degrees (using Degree—or after Version 3 in 1996—using °):
一直以来,您都可以以度数为单位明确给出参数(使用 Degree 或在 1996 年的 Version 3 之后使用 °):
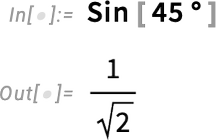
But a different convention would just say that the argument to Sin should always be interpreted as being in degrees, even if it’s just a plain number. Calculators would often have a physical switch that globally toggles to this convention. And while that might be OK if you are just doing a small calculation and can physically see the switch, nothing like that would make any sense at all in our system. But still, particularly in elementary mathematics, one might want a “degrees version” of trigonometric functions. And in Version 14.1 we’ve introduced these:
但另一种约定是, Sin 的参数应始终被解释为度数,即使它只是一个普通的数字。计算器通常会有一个物理开关,可以在全局范围内切换到这一约定。如果你只是在做一个小计算,并能看到物理开关,那么这样做可能没问题,但在我们的系统中,这样做没有任何意义。不过,特别是在初等数学中,人们还是可能需要三角函数的 "度数版本"。在 14.1 版中,我们引入了这些功能:
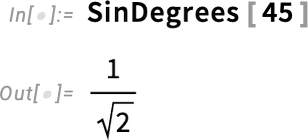
One might think this was somewhat trivial. But what’s nontrivial is that the “degrees trigonometric functions” are consistently integrated throughout the system. Here, for example, is the period in SinDegrees:
人们可能会认为这有些微不足道。但不难理解的是,"度三角函数 "在整个系统中都是一致的。例如,这里是 SinDegrees 中的周期:
You can take the integral as well
您也可以进行积分

and the messiness of this form shows why for more than three decades we’ve just dealt with Sin[x] and radians.
这种形式的混乱说明了为什么三十多年来我们只处理 Sin [x] 和弧度。
Fixed Points and Stability for Differential and Difference Equations
微分方程和差分方程的定点和稳定性
All sorts of differential equations have the feature that their solutions exhibit fixed points. It’s always in principle been possible to find these by looking for points where derivatives vanish. But in Version 14.1 we now have a general, robust function that takes the same form of input as DSolve and finds all fixed points:
各种微分方程都有一个特点,即它们的解会出现固定点。原则上,我们总是可以通过寻找导数消失的点来找到这些点。但在 14.1 版中,我们现在有了一个通用的、强大的函数,它可以接受与 DSolve 相同形式的输入,并找到所有固定点:
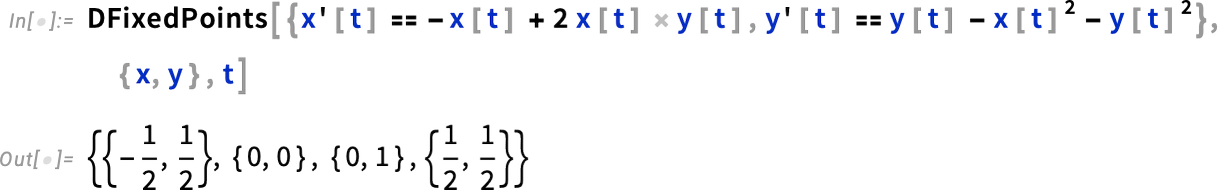
Here’s a stream plot of the solutions to our equations, together with the fixed points we’ve found:
下面是方程解的流图,以及我们找到的定点:
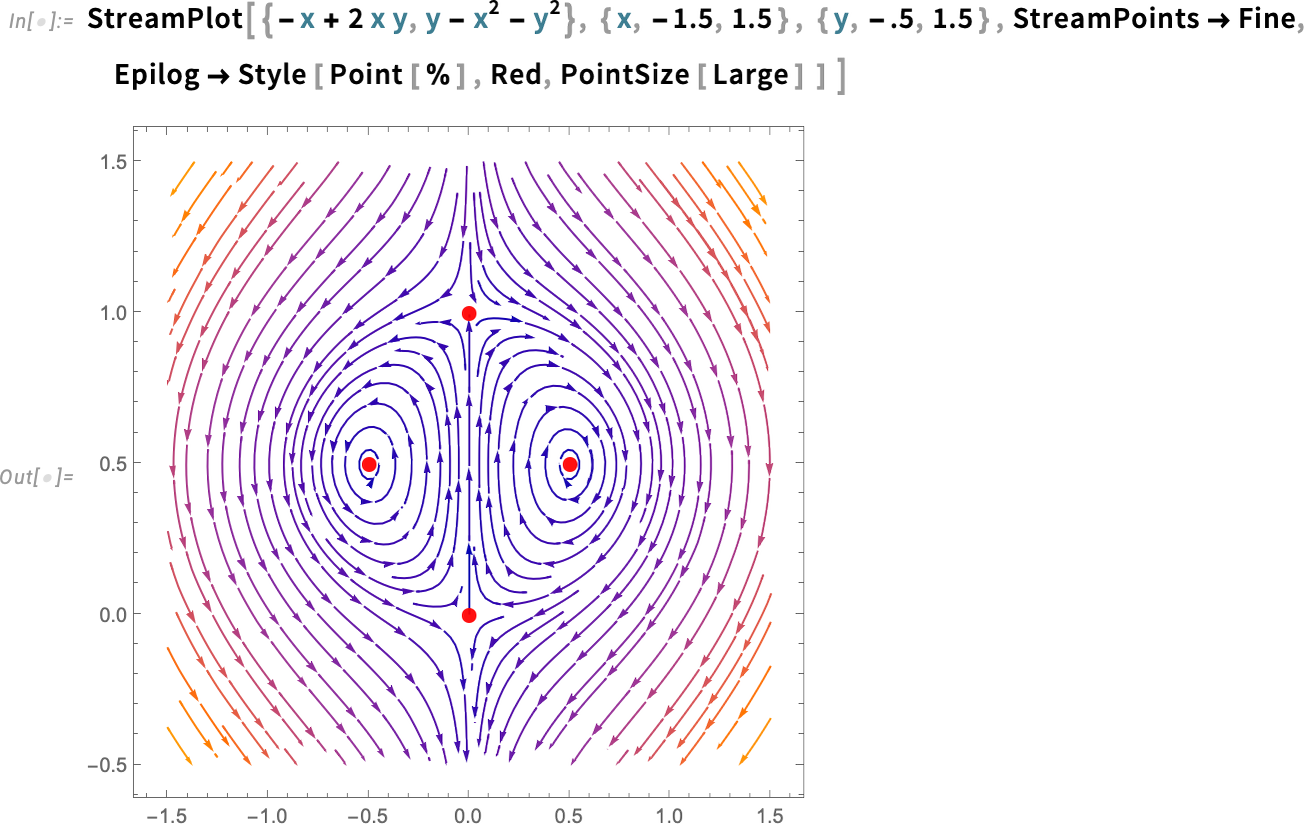
And we can see that there are two different kinds of fixed points here. The ones on the left and right are “stable” in the sense that solutions that start near them always stay near them. But it’s a different story for the fixed points at the top and bottom; for these, solutions that start nearby can diverge. The function DStabilityConditions computes fixed points, and specifies whether they are stable or not:
我们可以看到,这里有两种不同的固定点。左侧和右侧的定点是 "稳定 "的,因为从它们附近开始的解总是停留在它们附近。但顶部和底部的定点则不同;对于这些定点,在其附近开始的解可能会发散。函数 DStabilityConditions 可以计算固定点,并指定它们是否稳定:
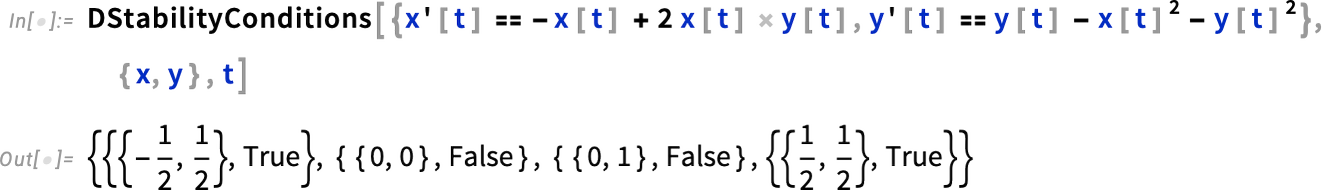
As another example, here are the Lorenz equations, which have one unstable fixed point, and two stable ones:
另一个例子是 洛伦兹方程,它有一个不稳定的定点和两个稳定的定点:
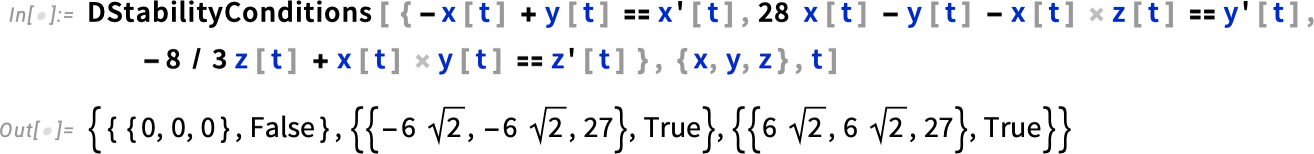
If your equations have parameters, their stability fixed points can depend on those parameters:
如果方程有参数,其稳定固定点可能取决于这些参数:
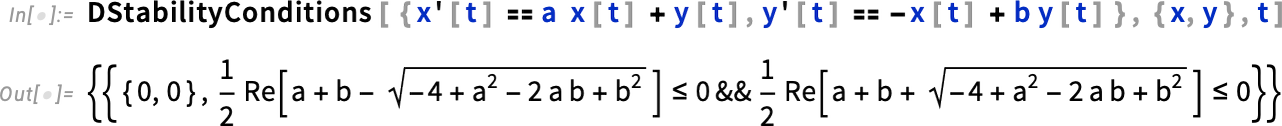
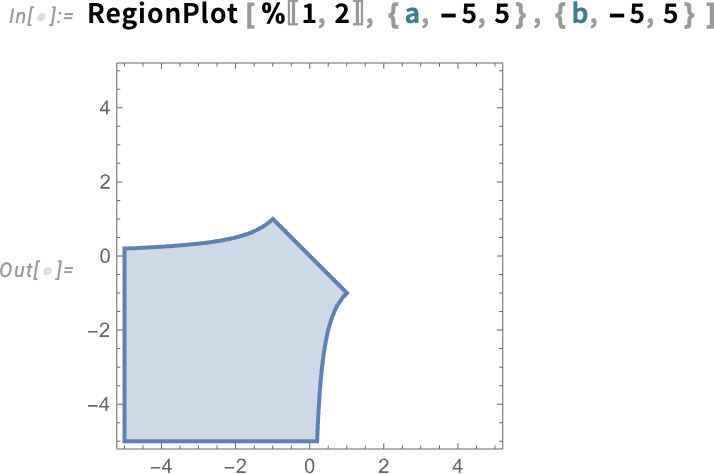
Extracting the conditions here, we can now plot the region of parameter space where this fixed point is stable:
提取这里的条件后,我们就可以绘制出该定点稳定的参数空间区域:
This kind of stability analysis is important in all sorts of fields, including dynamical systems theory, control theory, celestial mechanics and computational ecology.
这种稳定性分析在动力系统理论、控制理论、天体力学和计算生态学等各个领域都很重要。
And just as one can find fixed points and do stability analysis for differential equations, one can also do it for difference equations—and this is important for discrete dynamical systems, digital control systems, and for iterative numerical algorithms. Here’s a classic example in Version 14.1 for the logistic map:
正如我们可以为微分方程寻找定点和进行稳定性分析一样,我们也可以为差分方程寻找定点和进行稳定性分析--这对于离散动力系统、数字控制系统和迭代数值算法都很重要。下面是 14.1 版中关于逻辑图的一个经典示例:
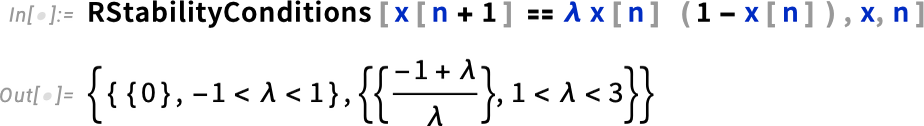
The Steady Advance of PDEs
稳步推进 PDE
Five years ago—in Version 11.3—we introduced our framework for symbolically representing physical systems using PDEs. And in every version since we’ve been steadily adding more and more capabilities. At this point we’ve now covered the basics of heat transfer, mass transport, acoustics, solid mechanics, fluid mechanics, electromagnetics and (one-particle) quantum mechanics. And with our underlying symbolic framework, it’s easy to mix components of all these different kinds.
五年前,在11.3版本中,我们推出了使用 PDE 符号表示物理系统的框架。此后的每个版本中,我们都在不断增加功能。目前,我们已经涵盖了传热、质量传输、声学、固体力学、流体力学、电磁学和(单粒子)量子力学的基础知识。有了我们的底层符号框架,就可以轻松混合所有这些不同类型的组件。
Our goal now is to progressively cover what’s needed for more and more kinds of applications. So in Version 14.1 we’re adding von Mises stress analysis for solid mechanics, electric current density models for electromagnetics and anisotropic effective masses for quantum mechanics.
我们现在的目标是逐步涵盖越来越多种类应用所需的内容。因此,在 14.1 版中,我们为固体力学添加了冯米塞斯应力分析,为电磁学添加了电流密度模型,为量子力学添加了各向异性有效质量。
So as an example of what’s now possible, here’s a piece of geometry representing a spiral inductor of the kind that might be used in a modern MEMS device:
因此,作为现在可能实现的一个例子,这里有一个几何图形,代表现代 MEMS 设备中可能使用的那种螺旋电感器:

Let’s define our variables—voltage and position:
让我们定义我们的变量--电压和位置:
And let’s specify parameters—here just that the material we’re going to deal with is copper:
让我们指定参数--这里只指定我们要处理的材料是铜:
Now we’re in a position to set up the PDE for this system, making use of the new constructs ElectricCurrentPDEComponent and ElectricCurrentDensityValue:
现在,我们可以利用新的结构 ElectricCurrentPDEComponent 和 ElectricCurrentDensityValue 为这个系统建立 PDE:

All it takes to solve this PDE for the voltage is then:
那么,只需求解这个电压的 PDE 即可:

From the voltage we can compute the current density
根据电压,我们可以计算出电流密度
and then plot it (and, yes, the current tends to avoid the corners):
然后绘制它(是的,电流往往会避开角落):

Symbolic Biomolecules and Their Visualization
符号生物分子及其可视化
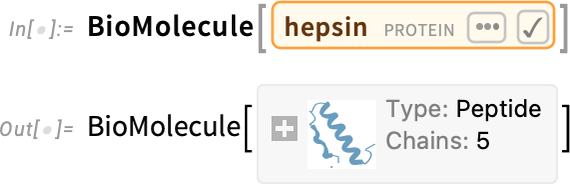
Ever since Version 12.2 we’ve had the ability to represent and manipulate bio sequences of the kind that appear in DNA, RNA and proteins. We’ve also been able to do things like import PDB (Protein Data Bank) files and generate graphics from them. But now in Version 14.1 we’re adding a symbolic BioMolecule construct, to represent the full structure of biomolecules:
自从12.2版开始,我们就有能力表示和处理 DNA、RNA 和蛋白质中出现的生物序列。我们还可以导入 PDB(蛋白质数据库)文件并从中生成图形。现在,我们在 14.1 版中添加了符号 BioMolecule 结构,以表示生物分子的完整结构:
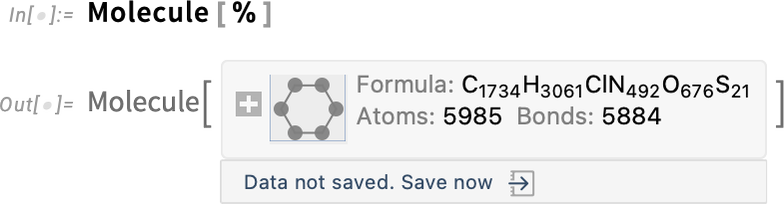
Ultimately this is “just a molecule” (and in this case its data is so big it’s not by default stored locally in your notebook):
归根结底,这 "只是一个分子"(在这种情况下,其数据量非常大,默认情况下不会存储在本地笔记本中):
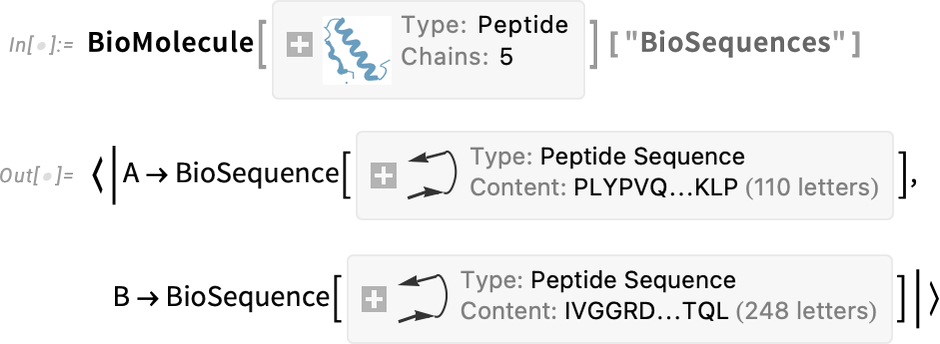
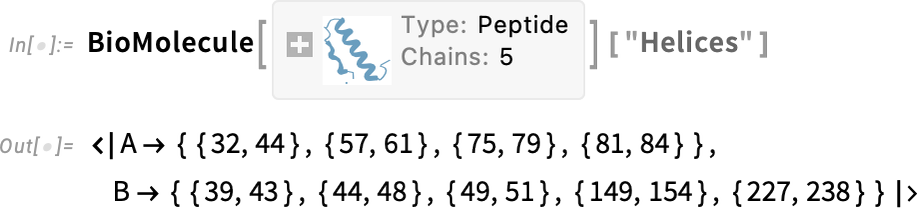
But what BioMolecule does is also to capture the “higher-order structure” of the molecule, for example how it’s built up from distinct chains, where structures like α-helices occur in these, and so on. For example, here are the two (bio sequence) chains that appear in this case:
但是, BioMolecule 还可以捕捉分子的 "高阶结构",例如,分子是如何由不同的链构建而成的,其中出现了 α 螺旋等结构,等等。例如,下面是本案例中出现的两条(生物序列)链:
And here are where the α-helices occur:
这里就是 α 螺旋出现的地方:
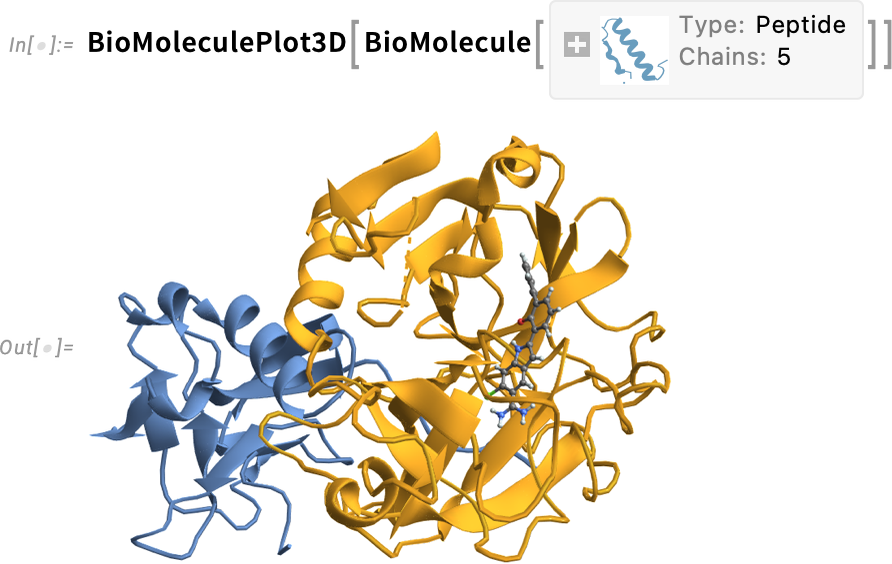
What about visualization? Well, there’s BioMoleculePlot3D for that:
可视化如何?有 BioMoleculePlot3D 可以解决这个问题:
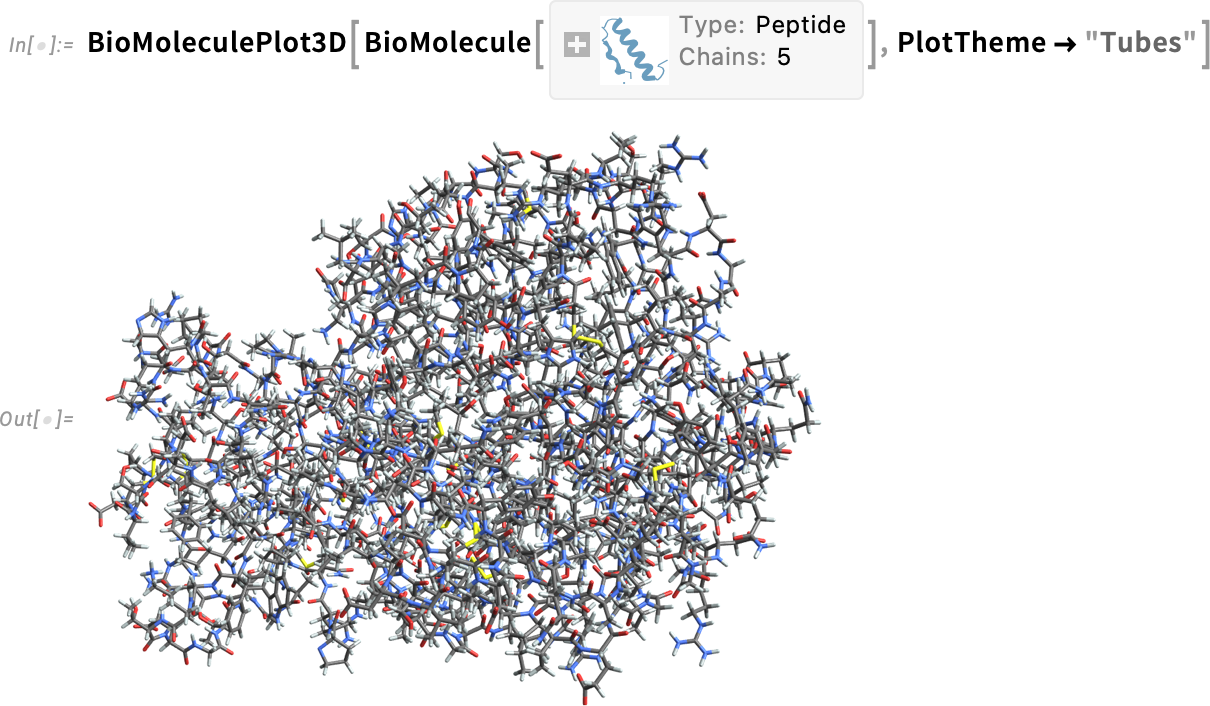
There are different “themes” you can use for this:
为此,您可以使用不同的 "主题":

Here’s a raw-atom-level view:
下面是原始原子级别的视图:
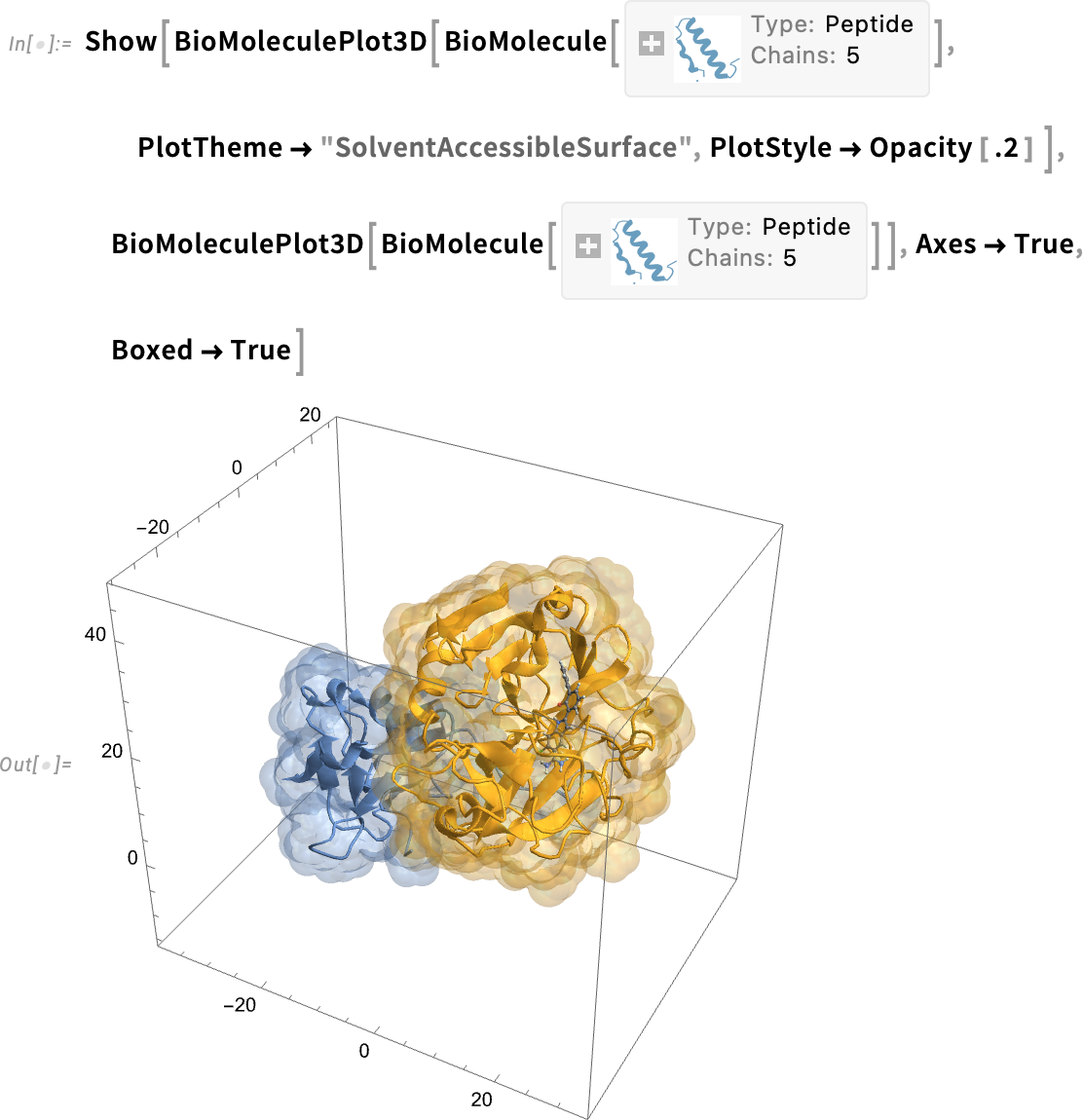
You can combine the views—and for example add coordinate values (specified in angstroms):
您可以合并视图,例如添加坐标值(以埃为单位):
You can also specify “color rules” that define how particular parts of the biomolecule should be rendered:
您还可以指定 "颜色规则",定义生物大分子特定部分的渲染方式:

But the structure here isn’t just something you can make graphics out of; it’s also something you can compute with. For example, here’s a geometric region formed from the biomolecule:
但是,这里的结构不仅仅是你可以制作图形的东西,也是你可以计算的东西。例如,这是生物分子形成的几何区域:

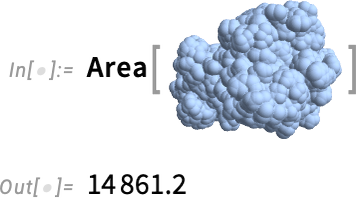
And this computes its surface area (in square angstroms):
这样就计算出了它的表面积(以平方埃为单位):
The Wolfram Language has built-in data on a certain number of proteins. But you can get data on many more proteins from external sources—specifying them with external identifiers:
Wolfram 语言内置了一定数量的蛋白质数据。不过,您可以从外部来源获取更多蛋白质的数据--使用外部标识符来指定它们:
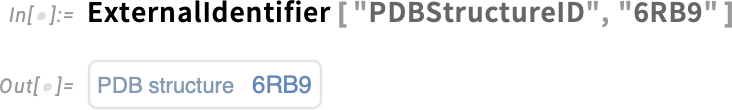

When you get a protein—say from an external source—it’ll often come with a 3D structure specified, for example as deduced from experimental measurements. But even without that, Version 14.1 will attempt to find at least an approximate structure—by using machine-learning-based protein-folding methods. As an example, here’s a random bio sequence:
当你从外部获取蛋白质时,通常会附带指定的三维结构,例如通过实验测量推导出的结构。但即使没有三维结构,14.1 版也会尝试使用基于机器学习的蛋白质折叠方法,至少找到一个近似结构。举例来说,下面是一个随机的生物序列:

If you make a BioMolecule out of this, a “predicted” 3D structure will be generated:
如果用它制作一个 BioMolecule ,就会生成一个 "预测的 "三维结构:

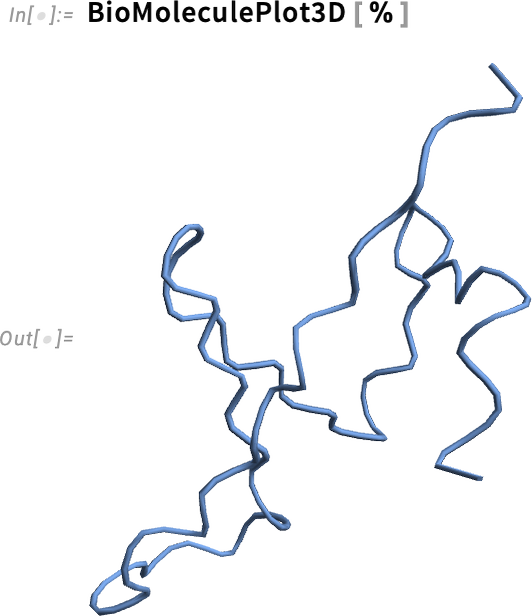
Here’s a visualization of this structure—though more work would be needed to determine how it’s related to what one might actually observe experimentally:
下面是这种结构的可视化图示--不过,要确定它与实验观察到的实际情况之间的关系,还需要做更多的工作:
Optimizing Neural Nets for GPUs and NPUs
为 GPU 和 NPU 优化神经网络
Many computers now come with GPU and NPU hardware accelerators for machine learning, and in Version 14.1 we’ve added more support for these. Specifically, on macOS (Apple Silicon) and Windows machines, built-in functions like ImageIdentify and SpeechRecognize now automatically use CoreML (Neural Engine) and DirectML capabilities—and the result is typically 2X to 10X faster performance.
现在,许多计算机都配备了用于机器学习的 GPU 和 NPU 硬件加速器,我们在 14.1 版中增加了对这些加速器的支持。具体来说,在 macOS(Apple Silicon)和 Windows 机器上, ImageIdentify 和 SpeechRecognize 等内置函数现在可以自动使用 CoreML(神经引擎)和 DirectML 功能,而且性能通常会提高 2 到 10 倍。
We’ve always supported explicit CUDA GPU acceleration, for both training and inference. But in Version 14.1 we now support CoreML and DirectML acceleration for inference tasks with explicitly specified neural nets. But whereas this acceleration is now the default for built-in machine-learning-based functions, for explicitly specified models the default isn’t yet the default.
我们一直支持显式 CUDA GPU 加速,用于训练和推理。但在 14.1 版中,我们现在支持 CoreML 和 DirectML 加速,用于明确指定神经网络的推理任务。虽然这种加速现在是基于机器学习的内置函数的默认设置,但对于明确指定的模型,默认设置还不是默认设置。
So, for example, this doesn’t use GPU acceleration:
因此,举例来说,它不会使用 GPU 加速:

But you can explicitly request it—and then (assuming all features of the model can be accelerated) things will typically run significantly faster:
但您可以明确提出请求,然后(假设模型的所有功能都可以加速),运行速度通常会大大加快:

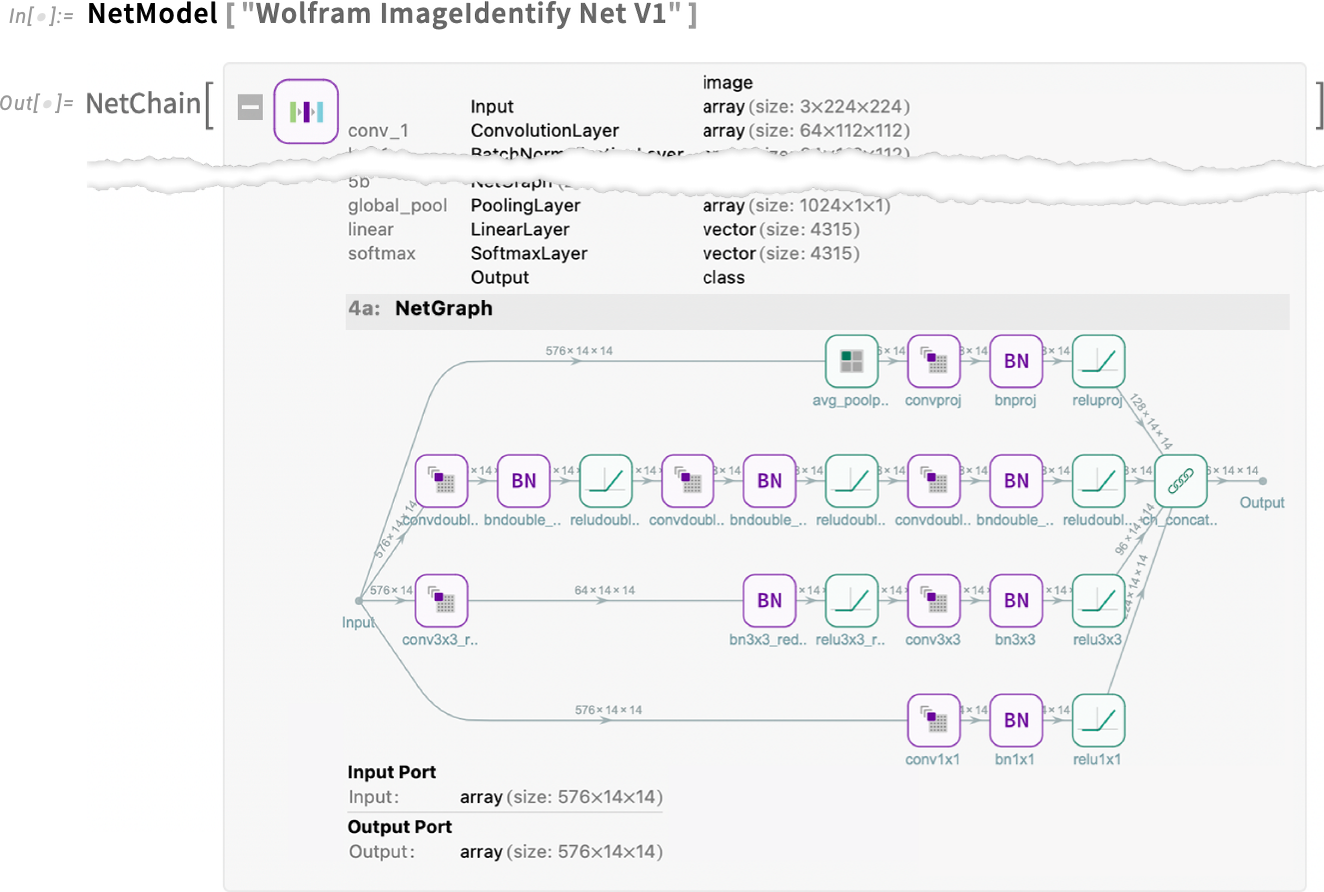
We’re continually sprucing up our infrastructure for machine learning. And as part of that, in Version 14.1 we’ve enhanced our diagrams for neural nets to make layers more visually distinct—and to immediately produce diagrams suitable for publication:
我们正在不断改进机器学习的基础架构。作为其中的一部分,我们在 14.1 版中增强了神经网络的图表功能,使图层在视觉上更加分明,并能立即生成适合出版的图表:
The Statistics of Dates 日期统计
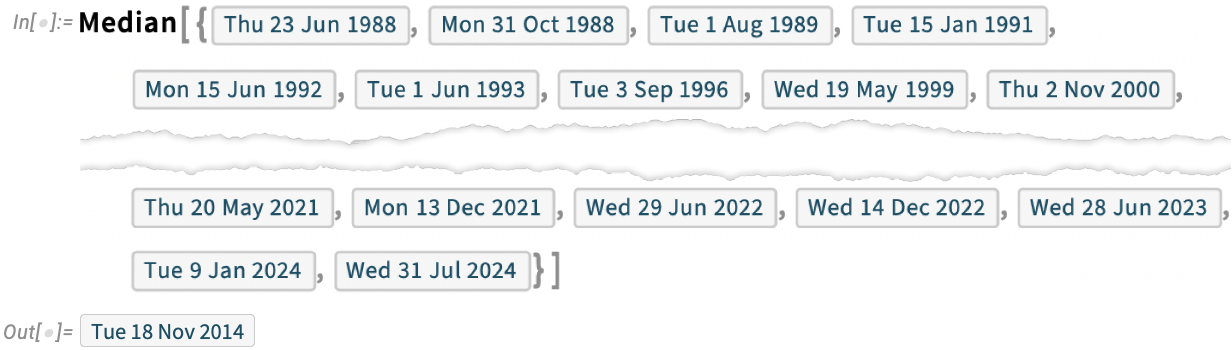
We’ve been releasing versions of what’s now the Wolfram Language for 36 years. And looking at that whole collection of release dates, we can ask statistical questions. Like “What’s the median date for all the releases so far?” Well, in Version 14.1 there’s a direct way to answer that—because statistical functions like Median now just immediately work on dates:
我们已经发布了 36 年的 Wolfram 语言版本。纵观这些版本的发布日期,我们可以提出一些统计问题。比如 "迄今为止所有版本的发布日期中位数是多少?"在 14.1 版中,我们有了一个直接的方法来回答这个问题--因为像 Median 这样的统计函数现在可以立即处理日期问题:
What if we ask about all 7000 or so functions in the Wolfram Language? Here’s a histogram of when they were introduced:
如果我们询问一下 Wolfram 语言中所有 7000 多个函数的情况会怎样?以下是这些函数推出时间的柱状图:
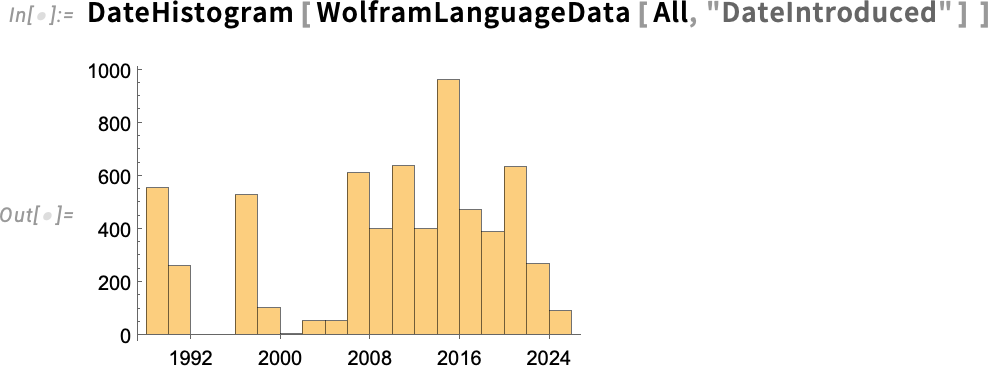
And now we can compute the median, showing quantitatively that, yes, Wolfram Language development has speeded up:
现在,我们可以计算出中位数,从数量上说明,Wolfram 语言的开发速度确实加快了:
Dates are a bit like numbers, but not quite. For example, their “zero” shifts around depending on the calendar. And their granularity is more complicated than precision for numbers. In addition, a single date can have multiple different representations (say in different calendars or with different granularities). But it nevertheless turns out to be possible to define many kinds of statistics for dates. To understand these statistics—and to compute them—it’s typically convenient to make one’s whole collection of dates have the same form. And in Version 14.1 this can be achieved with the new function ConformDates (which here converts all dates to the format of the first one listed):
日期有点像数字,但又不完全一样。例如,日期的 "零 "会根据日历的不同而变化。日期的粒度比数字的精度更复杂。此外,一个日期可以有多种不同的表示方法(比如在不同的日历中或以不同的粒度表示)。尽管如此,我们还是可以为日期定义多种统计量。为了理解这些统计数据并进行计算,通常需要使整个日期集合具有相同的形式。在 14.1 版中,新函数 ConformDates (该函数将所有日期转换为第一个列出的日期的格式)可以实现这一目的:

By the way, in Version 14.1 the whole pipeline for handling dates (and times) has been dramatically speeded up, most notably conversion from strings, as needed in the import of dates.
顺便提一下,在 14.1 版中,处理日期(和时间)的整个流程都大大加快了,最明显的是从字符串转换的速度,这在导入日期时是需要的。
The concept of doing statistics on dates introduces another new idea: date (and time) distributions. And in Version 14.1 there are two new functions DateDistribution and TimeDistribution for defining such distributions. Unlike for numerical (or quantity) distributions, date and time distributions require the specification of an origin, like Today, as well as of a scale, like "Days":
对日期进行统计的概念引入了另一个新思路:日期(和时间)分布。在 14.1 版中,有两个新函数 DateDistribution 和 TimeDistribution 用于定义此类分布。与数值(或数量)分布不同,日期和时间分布需要指定原点(如 Today )和刻度(如 "Days" ):

But given this symbolic specification, we can now do operations just like for any other distribution, say generating some random variates:
但有了这个符号说明,我们现在就可以像对其他分布一样进行操作,比如生成一些随机变量:

Building Videos with Programs
用程序制作视频
Introduced in Version 6 back in 2007, Manipulate provides an immediate way to create an interactive “manipulable” interface. And it’s been possible for a long time to export Manipulate objects to video. But just what should happen in the video? What sliders should move in what way? In Version 12.3 we introduced AnimationVideo to let you make a video in which one parameter is changing with time. But now in Version 14.1 we have ManipulateVideo which lets you create a video in which many parameters can be varied simultaneously. One way to specify what you want is to say for each parameter what value it should get at a sequence of times (by default measured in seconds from the beginning of the video). ManipulateVideo then produces a smooth video by interpolating between these values:
早在 2007 年 Version 6 中引入的 Manipulate 提供了一种创建交互式 "可操作 "界面的直接方法。将 Manipulate 对象导出到视频中也早已成为可能。但是,视频中应该发生什么?哪些滑块应以何种方式移动?在12.3版中,我们引入了 AnimationVideo ,让您可以制作一个参数随时间变化的视频。但现在在 14.1 版中,我们有了 ManipulateVideo ,它可以让您创建同时改变多个参数的视频。指定所需参数的一种方法是说明每个参数在一系列时间(默认情况下以视频开始时的秒为单位)应得到的值。 ManipulateVideo 将在这些值之间进行插值,从而制作出流畅的视频:
(An alternative is to specify complete “keyframes” by giving operations to be done at particular times.)
(另一种方法是指定完整的 "关键帧",在特定时间进行特定操作)。
ManipulateVideo in a sense provides a “holistic” way to create a video by controlling a Manipulate. And in the last several versions we’ve introduced many functions for creating videos from “existing structures” (for example FrameListVideo assembles a video from a list of frames). But sometimes you want to build up videos one frame at a time. And in Version 14.1 we’ve introduced SowVideo and ReapVideo for doing this. They’re basically the analog of Sow and Reap for video frames. SowVideo will “sow” one or more frames, and all frames you sow will then be collected and assembled into a video by ReapVideo:
ManipulateVideo 在某种意义上提供了一种 "整体 "方法,通过控制 Manipulate 来创建视频。在过去的几个版本中,我们引入了许多从 "现有结构 "创建视频的功能(例如, FrameListVideo 可从帧列表中组合视频)。但有时您需要逐帧创建视频。在 14.1 版中,我们引入了 SowVideo 和 ReapVideo 来实现这一目的。它们基本上与视频帧的 Sow 和 Reap 类似。 SowVideo 将 "播种 "一个或多个帧,然后您播种的所有帧将被 ReapVideo 收集并组合成视频:
One common application of SowVideo/ReapVideo is to assemble a video from frames that are programmatically picked out by some criterion from some other video. So, for example, this “sows” frames that contain a bird, then “reaps” them to assemble a new video.
SowVideo / ReapVideo 的一个常见应用是从其他视频中通过某种标准以编程方式挑选出的帧来组装视频。因此,举例来说,我们可以 "播种 "包含鸟类的帧,然后 "收获 "这些帧来组装新的视频。
Another way to programmatically create one video from another is to build up a new video by progressively “folding in” frames from an existing video—which is what the new function VideoFrameFold does:
另一种通过编程从另一个视频创建一个视频的方法是,通过逐步 "折叠 "现有视频中的帧来创建一个新视频,这就是新函数 VideoFrameFold 的作用:
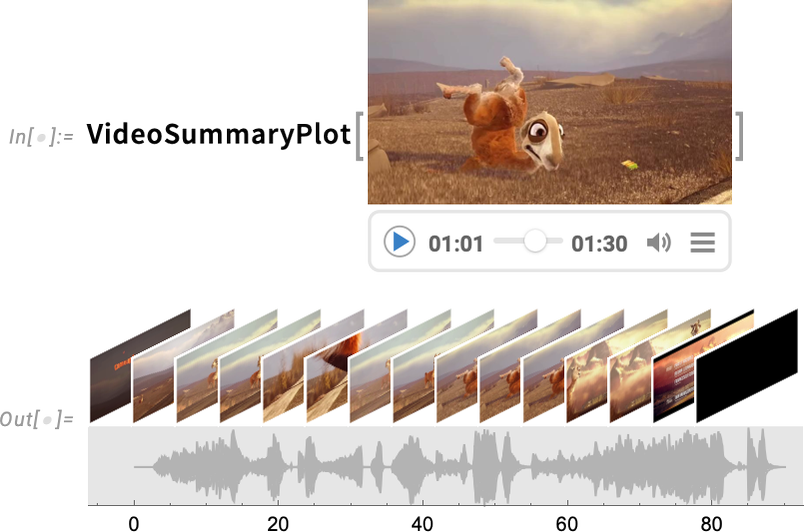
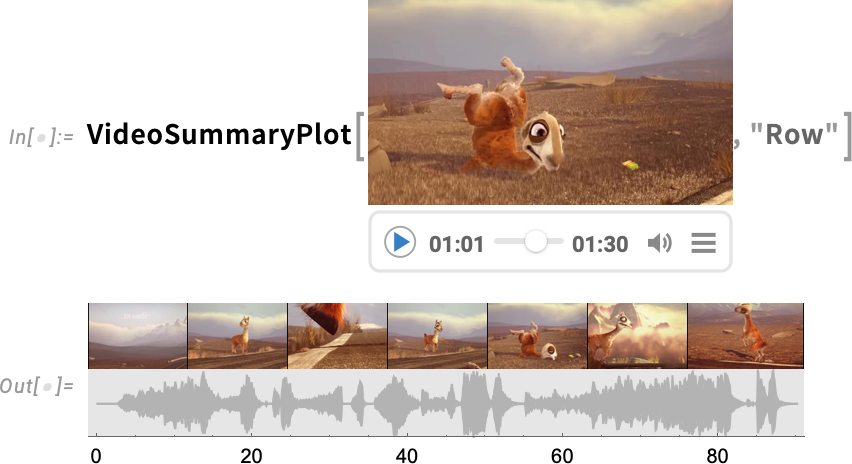
Version 14.1 also has a variety of new “convenience functions” for dealing with videos. One example is VideoSummaryPlot which generates various “at-a-glance” summaries of videos (and their audio):
14.1 版还新增了多种用于处理视频的 "便捷功能"。例如, VideoSummaryPlot 可以生成各种 "一目了然 "的视频(及其音频)摘要:
Another new feature in Version 14.1 is the ability to apply audio processing functions directly to videos:
14.1 版的另一项新功能是可以直接对视频应用音频处理功能:
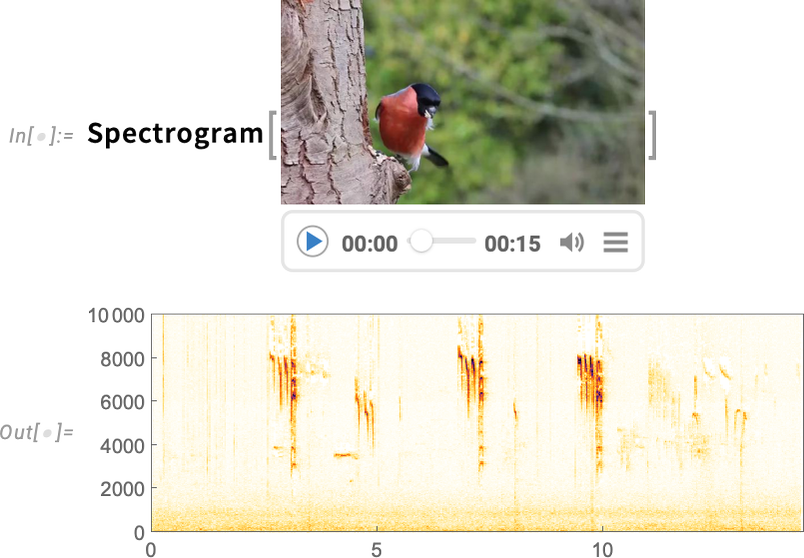
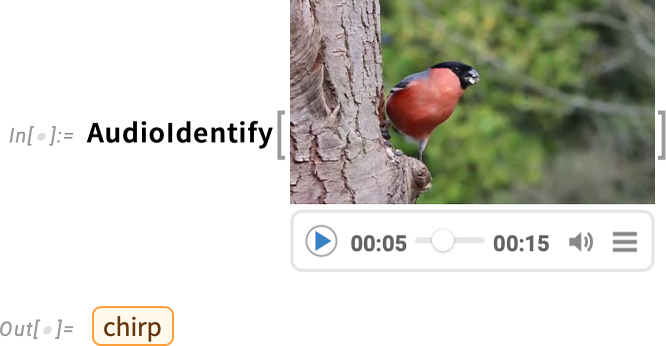
And, yes, it’s a bird:
没错,这是一只鸟:
Optimizing the Speech Recognition Workflow
优化语音识别工作流程
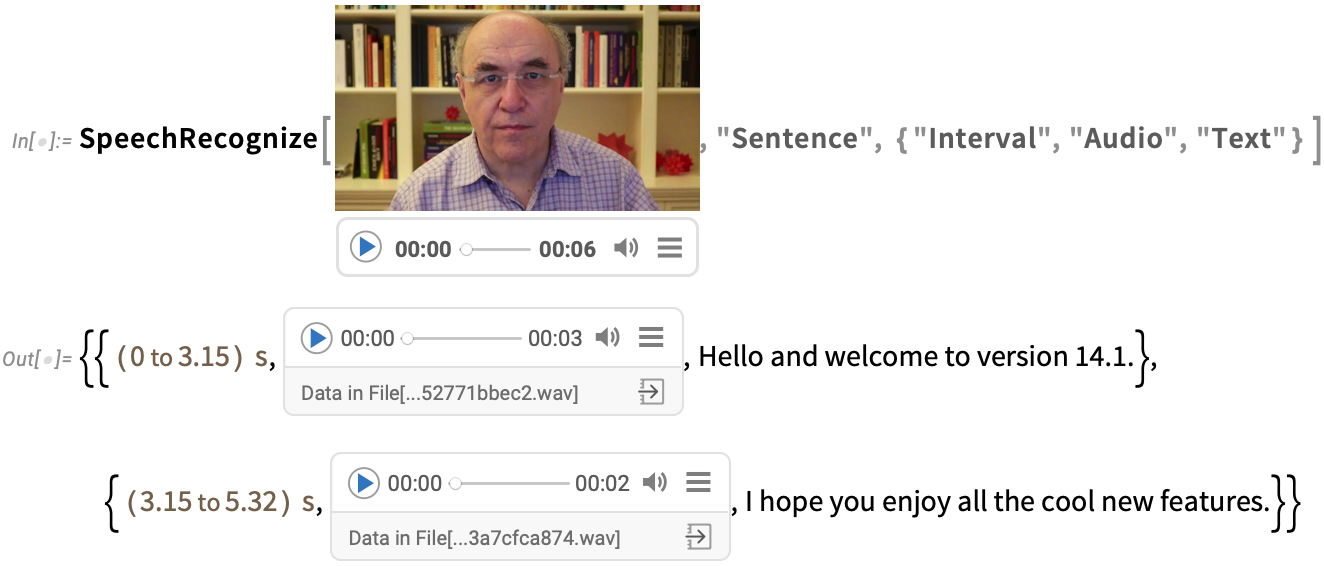
We first introduced SpeechRecognize in 2019 in Version 12.0. And now in Version 14.1 SpeechRecognize is getting a makeover.
我们于 2019 年在 12.0 版中首次引入了 SpeechRecognize 。现在,在 14.1 版中, SpeechRecognize 将得到彻底改变。
The most dramatic change is speed. In the past, SpeechRecognize would typically take at least as long to recognize a piece of speech as the duration of the speech itself. But now in Version 14.1, SpeechRecognize runs many tens of times faster, so you can recognize speech much faster than real time.
最显著的变化是速度。过去, SpeechRecognize 识别一段语音所需的时间通常至少与语音本身的持续时间相当。但现在在 14.1 版中, SpeechRecognize 的运行速度要快几十倍,因此您可以比实时更快地识别语音。
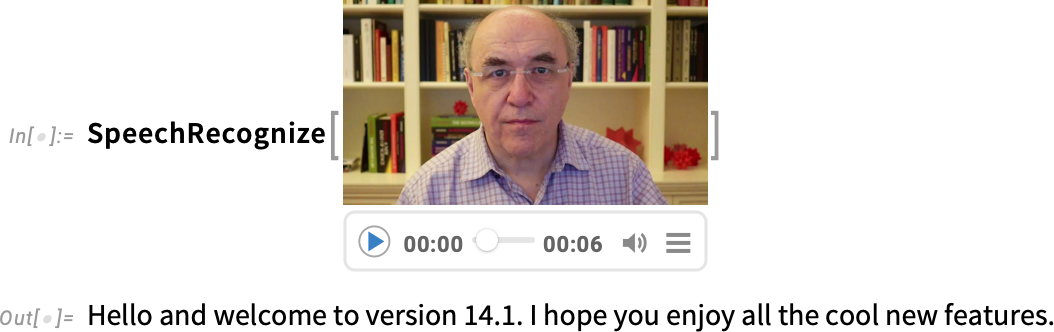
And what’s more, SpeechRecognize now produces full, written text, complete with capitalization, punctuation, etc. So here, for example, is a transcription of a little video:
此外, SpeechRecognize 现在可以生成完整的书面文本,包括大小写、标点符号等。例如,这里是小视频的转录:
There’s also a new function, VideoTranscribe, that will take a video, transcribe its audio, and insert the transcription back into the subtitle track of the video.
还有一个新功能 VideoTranscribe ,它可以获取视频、转录音频并将转录内容插入视频的字幕轨道。
And, by the way, SpeechRecognize runs entirely locally on your computer, without having to access a server (except maybe for updates to the neural net it’s using).
顺便提一下, SpeechRecognize 完全在您的计算机上本地运行,无需访问服务器(除了更新所使用的神经网络)。
In the past SpeechRecognize could only handle English. In Version 14.1 it can handle 100 languages—and can automatically produce translated transcriptions. (By default it produces transcriptions in the language you’ve specified with $Language.) And if you want to identify what language a piece of audio is in, LanguageIdentify now works directly on audio.
过去, SpeechRecognize 只能处理英语。在 14.1 版中,它可以处理 100 种语言,并且可以自动生成翻译转录。(默认情况下,它会以您用 $Language 指定的语言生成转录)。如果您想识别一段音频的语言, LanguageIdentify 现在可以直接在音频上工作。
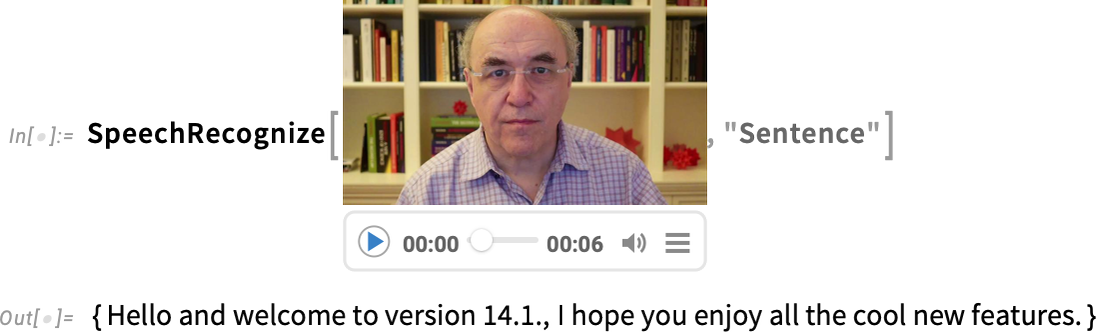
SpeechRecognize by default produces a single string of text. But it now also has the option to break up its results into a list, say of sentences:
SpeechRecognize 默认情况下只生成一个文本字符串。但现在它也可以将结果分成一个列表,例如句子:
And in addition to producing a transcription, SpeechRecognize can give time intervals or audio fragments for each element:
除了生成转录外, SpeechRecognize 还可以为每个元素提供时间间隔或音频片段:
Historical Geography Becomes Computable
历史地理变得可计算
History is complicated. But that doesn’t mean there isn’t much that can be made computable about it. And in Version 14.1 we’re taking a major step forward in making historical geography computable. We’ve had extensive geographic computation capabilities in the Wolfram Language for well over a decade. And in Version 14.1 we’re extending that to historical geography.
历史是复杂的。但这并不意味着没有什么是可以计算的。在 14.1 版中,我们在历史地理可计算性方面迈出了重要一步。十多年前,我们就已经在 Wolfram 语言中提供了广泛的地理计算功能。在 14.1 版中,我们将这一功能扩展至历史地理。
So now you can not only ask for a map of where the current country of Italy is, you can also ask to make a map of the Roman Empire in 100 AD:
因此,现在您不仅可以要求绘制当前意大利所在国家的地图,还可以要求绘制公元 100 年罗马帝国的地图:
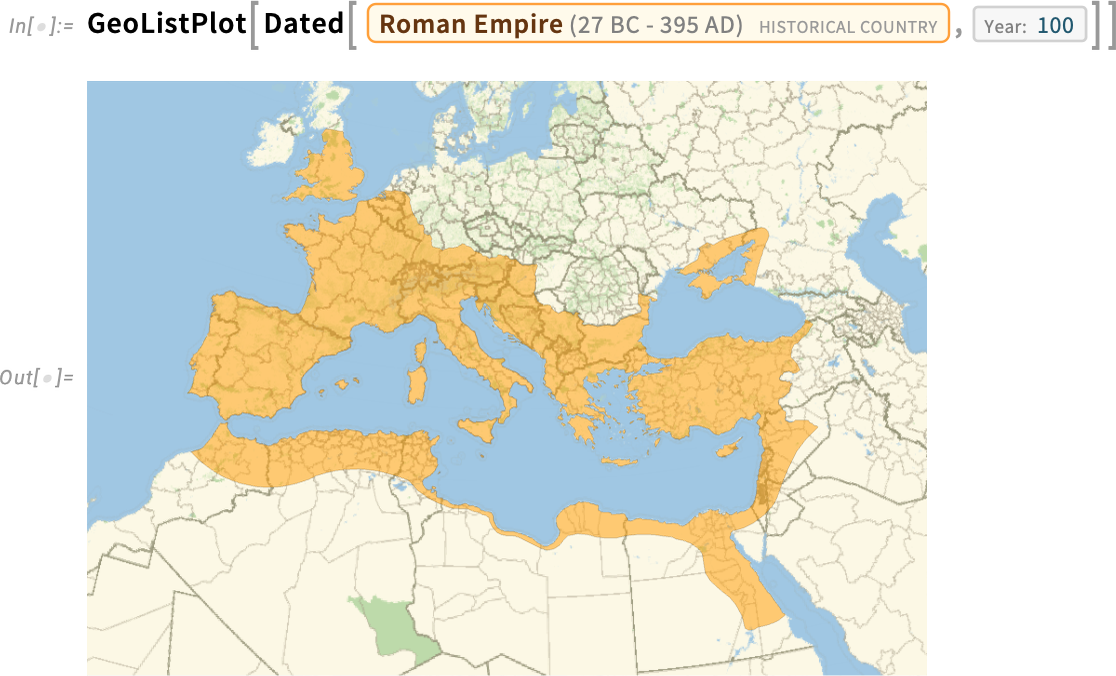
And “the Roman Empire in 100 AD” is now a computable entity. So you can ask for example what its approximate area was:
而 "公元 100 年的罗马帝国 "现在是一个可计算的实体。例如,你可以问它的面积大约是多少:

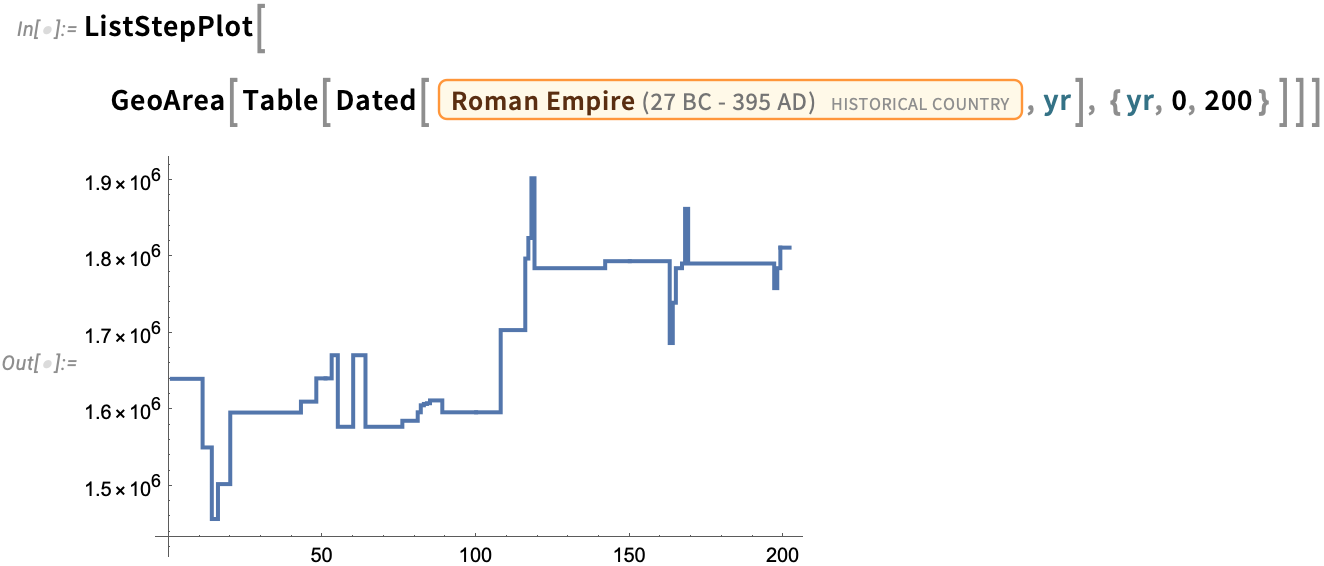
And you can even make a plot of how the area of the Roman Empire changed over the period from 0 AD to 200 AD:
您甚至还可以绘制出从公元 0 年到公元 200 年期间罗马帝国面积的变化图:
We’ve been building our knowledgebase of historical geography for many years. Of course, country borders may be disputed, and—particularly in the more distant past—may not have been well defined. But by now we’ve accumulated computable data on basically all of the few thousand known historical countries. Still—with history being complicated—it’s not surprising that there are all sorts of often subtle issues.
多年来,我们一直在建立我们的历史地理知识库。当然,国家边界可能存在争议,特别是在更遥远的过去,可能并没有得到很好的界定。但到目前为止,我们已经积累了几千个已知历史国家的可计算数据。尽管如此,历史是复杂的,存在各种微妙的问题也不足为奇。
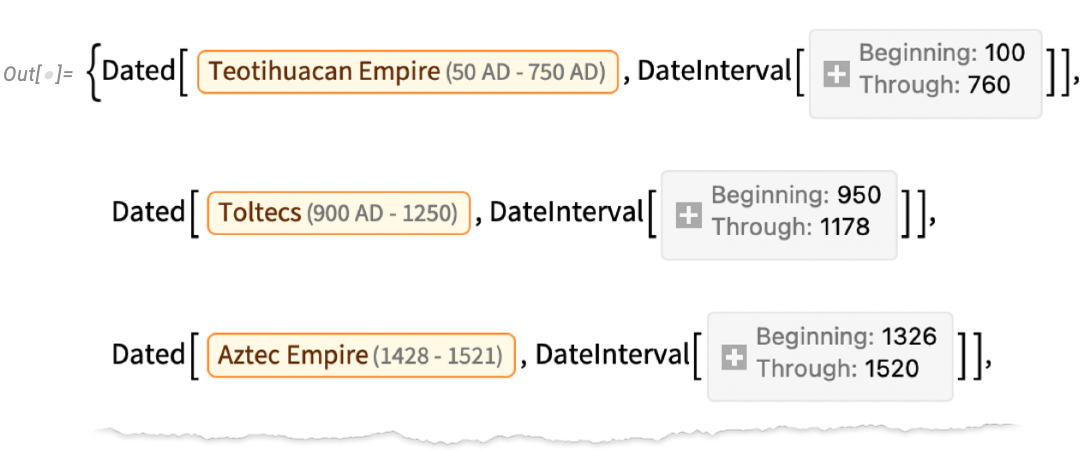
Let’s start by asking what historical countries the location that’s now Mexico City has been in. GeoIdentify gives the answer:
让我们先来看看现在的墨西哥城在历史上曾属于哪些国家。 GeoIdentify 给出了答案:

And already we see subtlety. For example, our historical country entities are labeled by their overall beginning and ending dates. But most of them covered Mexico City only for part of their existence. And here we can see what’s going on:
我们已经看到了微妙之处。例如,我们历史上的国家实体是按其总的开始和结束日期来标注的。但其中大部分国家仅在其存在的部分时间里覆盖了墨西哥城。在这里,我们可以看到发生了什么:
Often there’s subtlety in identifying what should count as a “different country”. If there was just an “acquisition” or a small “change of management” maybe it’s still the same country. But if there was a “dramatic reorganization”, maybe it’s a different country. Sometimes the names of countries (if they even had official names) give clues. But in general it’s taken lots of case-by-case curation, trying to follow the typical conventions used by historians of particular times and places.
在确定什么是 "不同的国家 "时,往往有一些微妙之处。如果只是 "收购 "或 "管理层的小变动",也许还是同一个国家。但如果是 "戏剧性的重组",也许就是另一个国家了。有时,国家名称(如果它们有正式名称的话)会提供一些线索。但总的来说,我们需要进行大量的个案整理,努力遵循特定时间和地点的历史学家所使用的典型惯例。
For London we see several “close-but-we-consider-it-a-different-country” issues—along with various confusing repeated conquerings and reconquerings:
在伦敦,我们看到了几个 "接近但我们认为是不同国家 "的问题,以及各种令人困惑的反复征服和重新征服:

Here’s a timeline plot of the countries that have contained London:
以下是包含伦敦的国家的时间轴图:
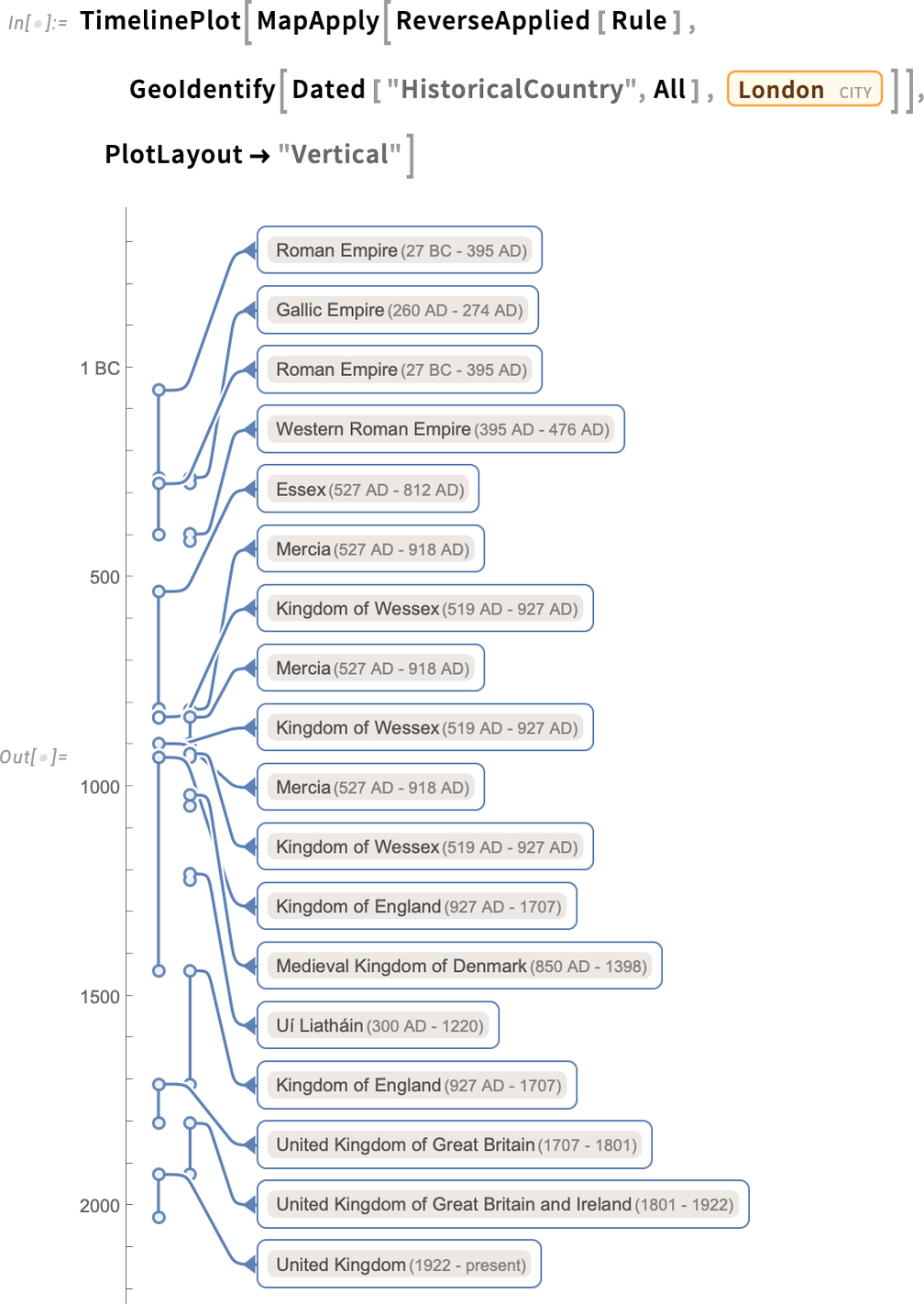
And because everything is computable, it’s easy to identify the longest contiguous segment here:
由于一切都可以计算,因此很容易确定这里最长的连续段:

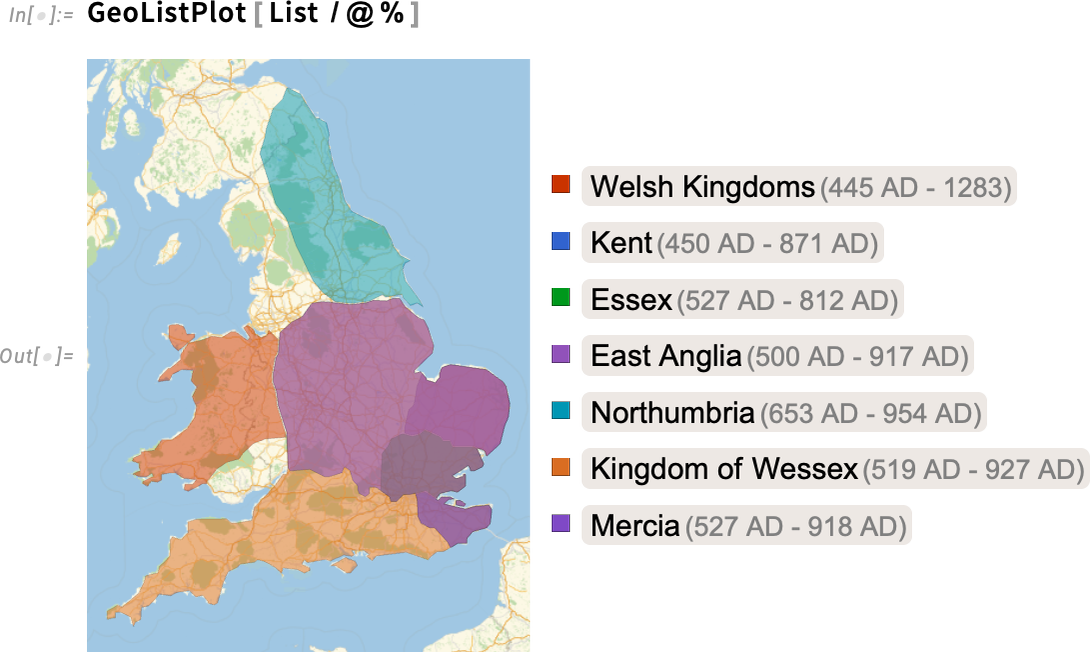
GeoIdentify can tell us what entities something like a city is inside. GeoEntities, on the other hand, can tell us what entities are inside something like a country. So, for example, this tells us what historical countries were inside (or at least overlapped with) the current boundaries of the UK in 800 AD:
GeoIdentify 可以告诉我们城市这样的实体在什么地方。另一方面, GeoEntities 可以告诉我们一个国家的内部有哪些实体。因此,举例来说,这可以告诉我们在公元 800 年,英国目前的疆界内有哪些历史上的国家(或至少与之重叠):

This then makes a map (the extra list makes these countries be rendered separately):
这样就能绘制出一张地图(额外的列表使这些国家能够单独呈现):
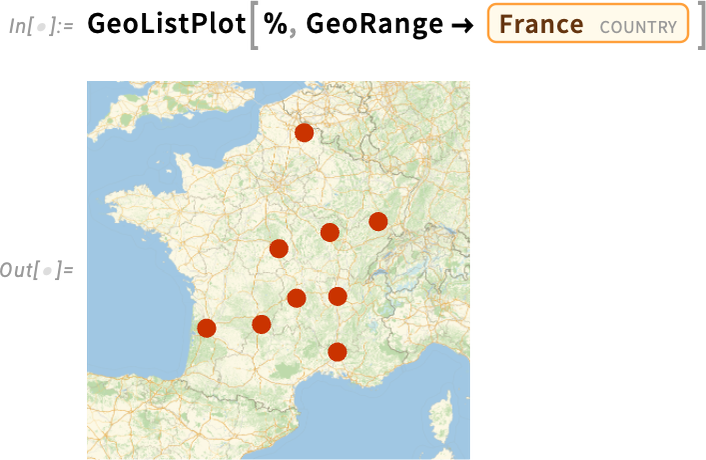
In the Wolfram Language we have data on quite a few kinds of historical entities beyond countries. For example, we have extensive data on military conflicts. Here we’re asking what military conflicts occurred within the borders of what’s now France between 200 BC and 200 AD:
在 Wolfram 语言中,除了国家之外,我们还拥有许多历史实体的数据。例如,我们有大量关于军事冲突的数据。这里我们要问的是,公元前 200 年至公元 200 年期间,在现在的法国境内发生了哪些军事冲突:

Here’s a map of their locations:
下面是他们的位置图:
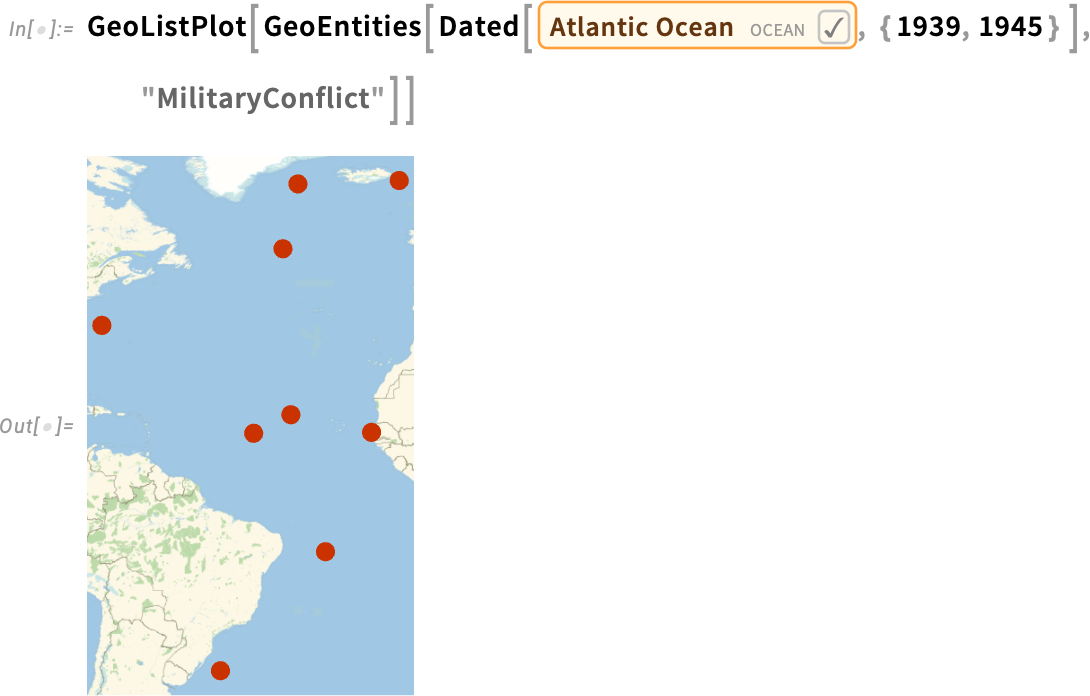
And here are conflicts in the Atlantic Ocean in the period 1939–1945:
这里是 1939-1945 年期间大西洋上的冲突:
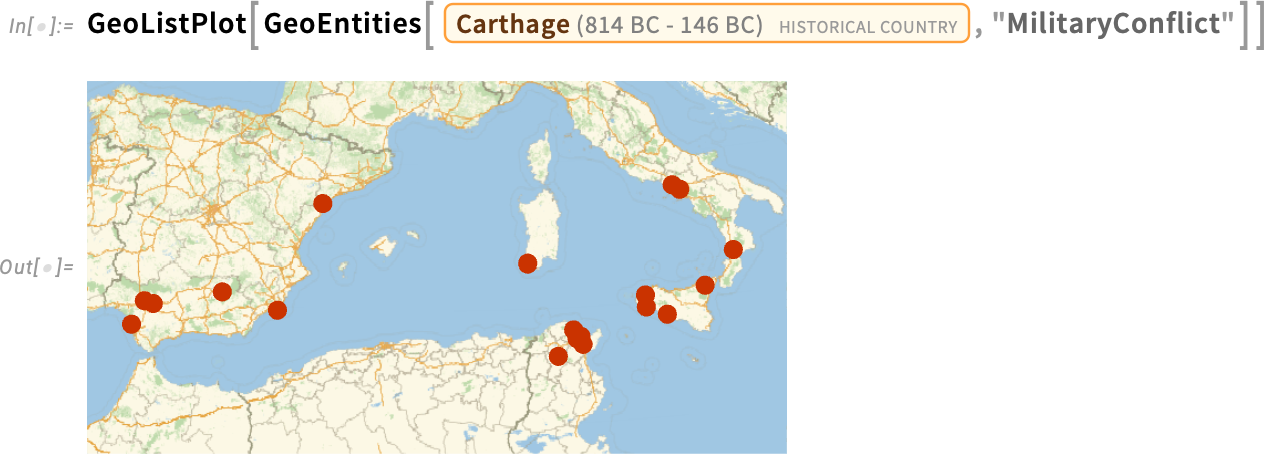
And—combining several things—here’s a map of conflicts that, at the time when they occurred, were within the region of what was then Carthage:
下面是一张冲突地图,这些冲突发生时都在当时的迦太基地区:
There are all sorts of things that we can compute from historical geography. For example, this asks for the (minimum) geo distance between the territory of the Roman Empire and the Han Dynasty in 100 AD:
我们可以从历史地理中计算出各种各样的东西。例如,我们需要计算公元 100 年罗马帝国与汉朝领土之间的(最小)地理距离:

But what about the overall minimum distance across all years when these historical countries existed? This gives the result for that:
那么,在这些历史国家存在的所有年份中,总的最小距离是多少呢?这就是结果:

Let’s compare this with a plot of these two entities:
让我们用这两个实体的曲线图来比较一下:
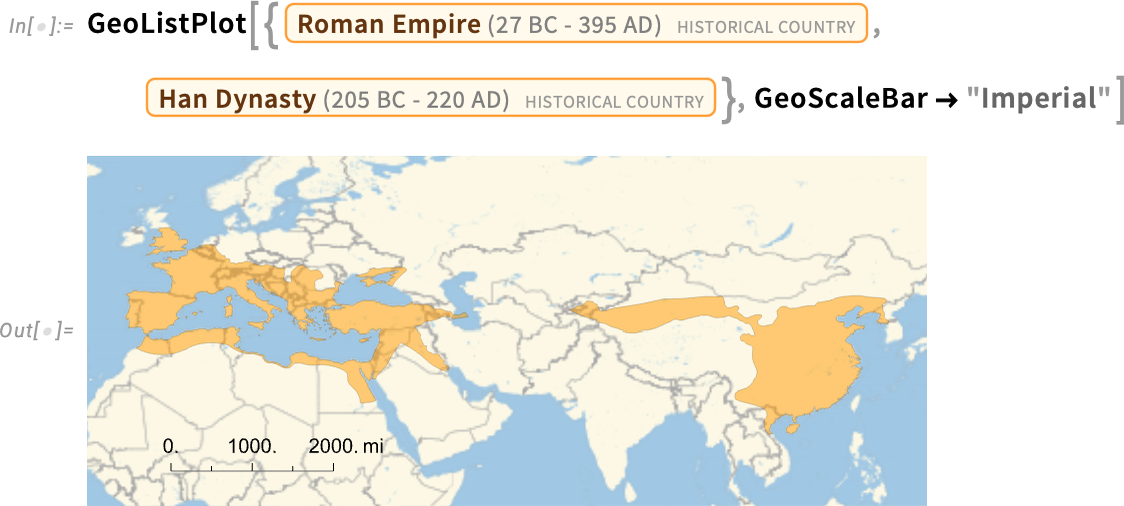
But there’s a subtlety here. What version of the Roman Empire is it that we’re showing on the map here? Our convention is by default to show historical countries “at their zenith”, i.e. at the moment when they had their maximum extent.
但这里有一个微妙之处。我们在地图上显示的是哪个版本的罗马帝国?我们的惯例是默认显示历史上国家的 "顶点",即它们达到最大程度的时候。
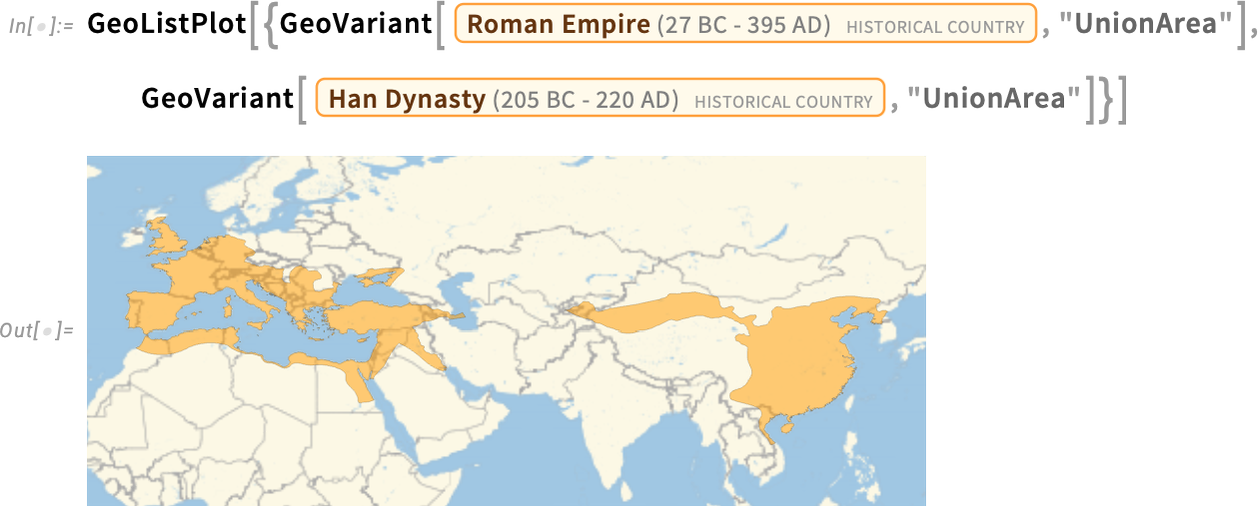
But what about other choices? Dated gives us a way to specify a particular date. But another possibility is to include in what we consider to be a particular historical country any territory that was ever part of that country, at any time in its history. And you can do this using GeoVariant[…, "UnionArea"]. In the particular case we’re showing here, it doesn’t make much difference, except that there’s more territory in Germany and Scotland included in the Roman Empire:
那么其他选择呢? Dated 为我们提供了一种指定特定日期的方法。但另一种可能性是,在我们认为是某个历史国家的范围内,包括该国历史上任何时期的任何领土。您可以使用 GeoVariant […, "UnionArea"] 来做到这一点。在我们这里展示的特定案例中,除了罗马帝国包含了更多的德国和苏格兰领土外,其他并无太大区别:
By the way, you can combine Dated and GeoVariant, to get things like “the zenith within a certain period” or “any territory that was included at any time within a period”. And, yes, it can get quite complicated. In a rather physics-like way you can think of the extent of a historical country as defining a region in spacetime—and indeed GeoVariant[…, "TimeSeries"] in effect represents a whole “stack of spacelike slices” in this spacetime region:
顺便说一下,您可以将 Dated 和 GeoVariant 结合起来,以获得 "某个时期内的天顶 "或 "某个时期内任何时间包含的任何领土 "等信息。是的,这可能会变得相当复杂。从物理学的角度来看,你可以把一个历史国家的范围看作是定义了一个时空区域--事实上, GeoVariant […, "TimeSeries"] 实际上代表了这个时空区域中的整个 "类似空间切片的堆叠":

And—though it takes a little while—you can use it to make a video of the rise and fall of the Roman Empire:
此外,虽然需要一点时间,但您可以用它来制作罗马帝国兴衰的视频:
Astronomical Graphics and Their Axes
天文图形及其轴线
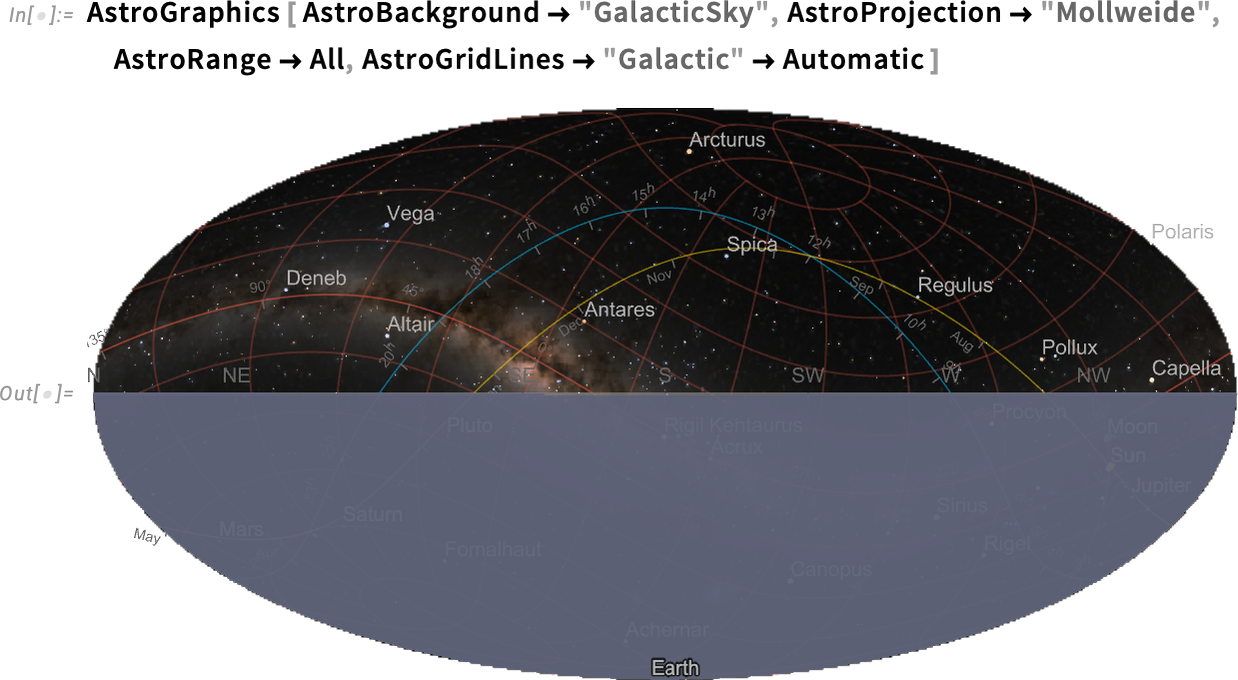
It’s complicated to define where things are in the sky. There are four main coordinate systems that get used in doing this: horizon (relative to local horizon), equatorial (relative to the Earth’s equator), ecliptic (relative to the orbit of the Earth around the Sun) and galactic (relative to the plane of the galaxy). And when we draw a diagram of the sky (here on white for clarity) it’s typical to show the “axes” for all these coordinate systems:
要确定事物在天空中的位置非常复杂。主要有四个坐标系:地平线(相对于本地地平线)、赤道(相对于地球赤道)、黄道(相对于地球绕太阳的轨道)和银河系(相对于银河系平面)。当我们绘制天空示意图时(为了清晰起见,这里用白色),通常会显示所有这些坐标系的 "轴线":
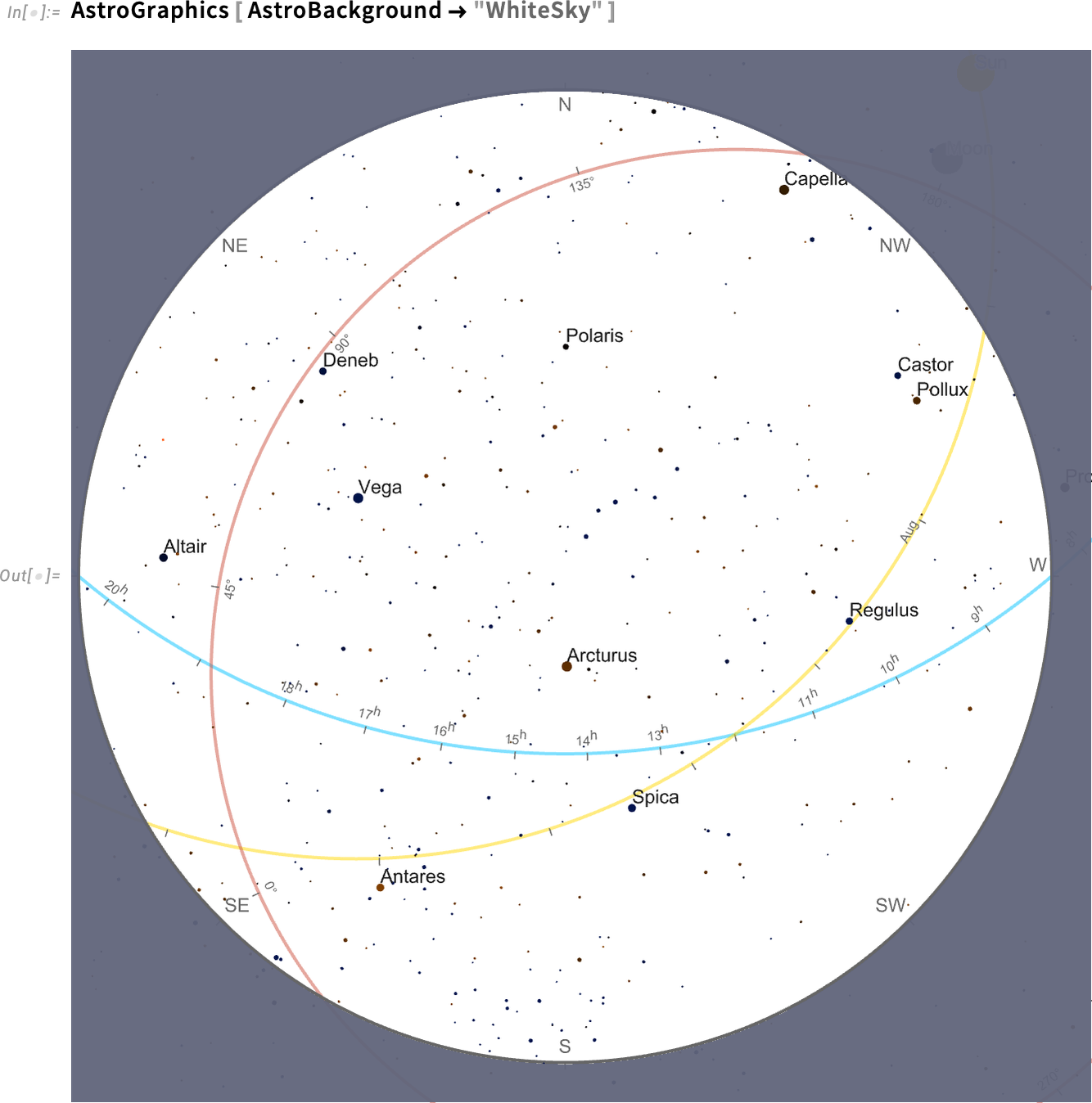
But here’s a tricky thing: how should those axes be labeled? Each one is different: horizon is most naturally labeled by things like cardinal directions (N, E, S, W, etc.), equatorial by hours in the day (in sidereal time), ecliptic by months in the year, and galactic by angle from the center of the galaxy.
但这里有一个棘手的问题:这些坐标轴应该如何标注?每条轴线都不一样:地平线最自然的标注方式是以红绿方位(北、东、南、西等)标注,赤道轴以一天中的小时数(恒星时)标注,黄道轴以一年中的月份标注,银河轴以与银河系中心的角度标注。
In ordinary plots axes are usually straight, and labeled uniformly (or perhaps, say, logarithmically). But in astronomy things are much more complicated: the axes are intrinsically circular, and then get rendered through whatever projection we’re using.
在普通绘图中,坐标轴通常是直的,并统一标注(或者说,按对数标注)。但在天文学中,情况要复杂得多:坐标轴本质上是圆形的,然后通过我们使用的投影进行渲染。
And we might have thought that such axes would require some kind of custom structure. But not in the Wolfram Language. Because in the Wolfram Language we try to make things general. And axes are no exception:
我们可能会认为,这种轴需要某种自定义结构。但在 Wolfram 语言中并非如此。因为在沃尔夫拉姆语言中,我们努力使事物具有通用性。轴也不例外:
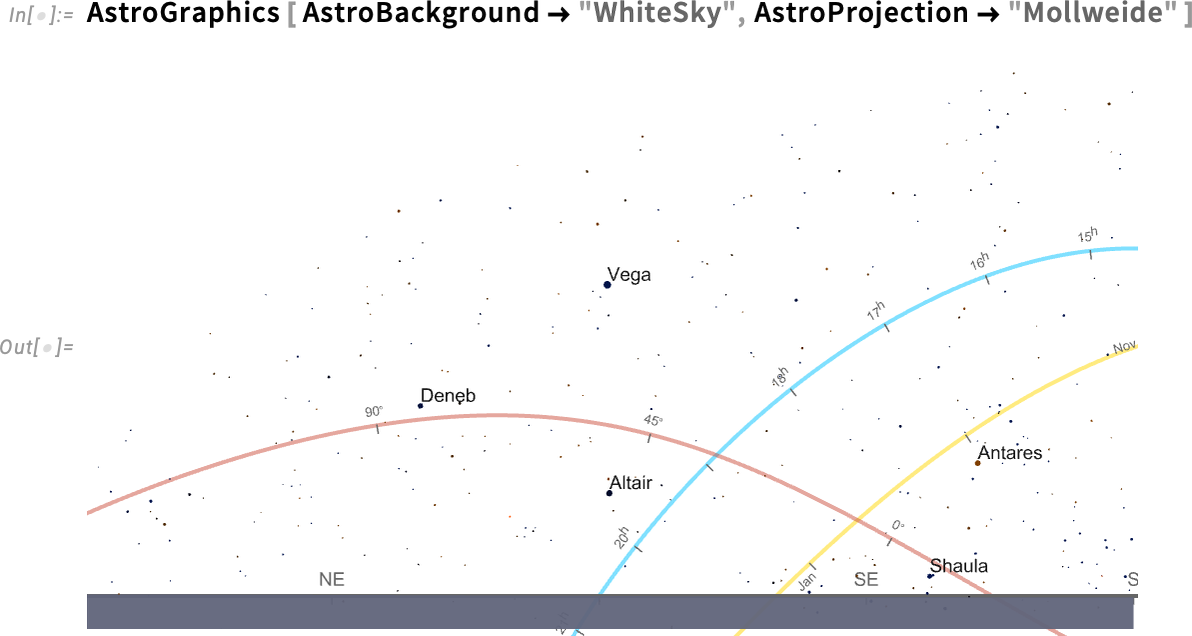
So in AstroGraphics all our various axes are just AxisObject constructs—that can be computed with. And so, for example, here’s a Mollweide projection of the sky:
因此,在 AstroGraphics 中,我们所有的轴都只是 AxisObject 结构,可以用它来计算。例如,这里是天空的 Mollweide 投影:
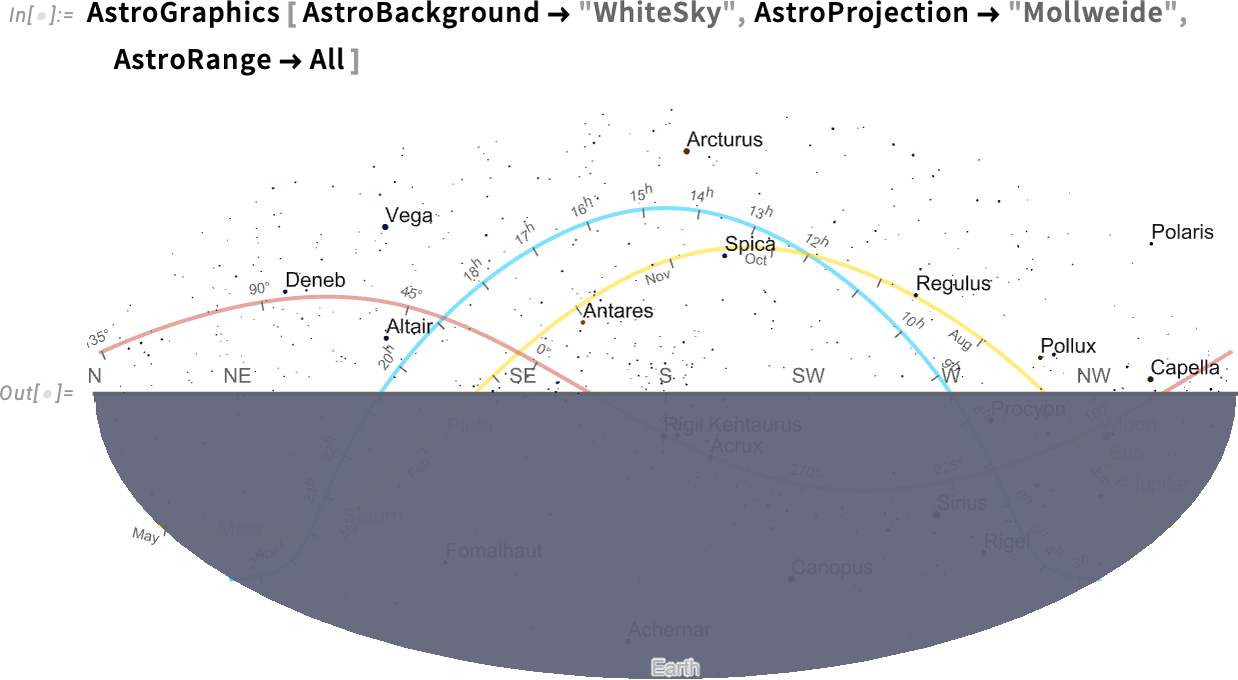
If we insist on “seeing the whole sky”, the bottom half is just the Earth (and, yes, the Sun isn’t shown because I’m writing this after it’s set for the day…):
如果我们坚持要 "看到整个天空",那么下半部分就是地球(是的,没有显示太阳,因为我是在太阳落山后写这篇文章的......):
Things get a bit wild if we start adding grid lines, here for galactic coordinates:
如果我们开始添加网格线,情况就会变得有点疯狂,这里是银河系坐标:
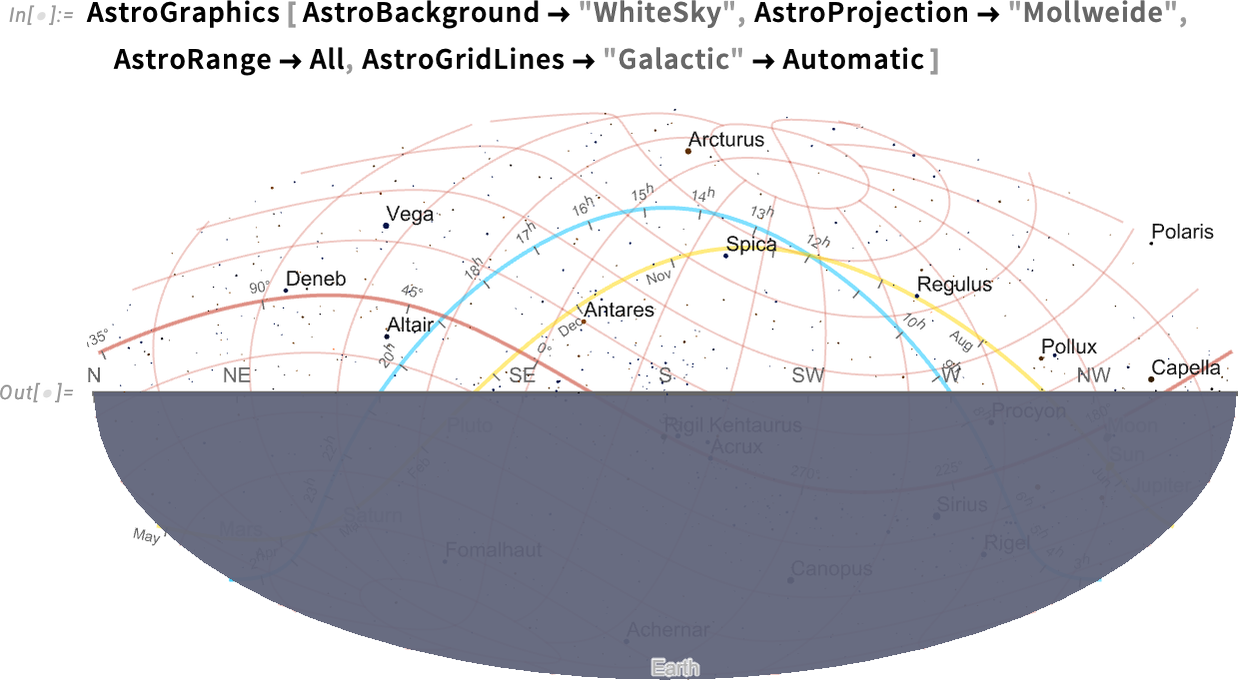
And, yes, the galactic coordinate axis is indeed aligned with the plane of the Milky Way (i.e. our galaxy):
是的,银河坐标轴确实与银河系(即我们的银河系)的平面对齐:
When Is Earthrise on Mars? New Level of Astronomical Computation
火星何时日出?天文计算的新水平
When will the Earth next rise above the horizon from where the Perseverance rover is on Mars? In Version 14.1 we can now compute this (and, yes, this is an “Earth time” converted from Mars time using the standard barycentric celestial reference system (BCRS) solar-system-wide spacetime coordinate system):
从 "坚毅 "号漫游车所在的火星上看,地球下一次升出地平线的时间是什么时候?在 14.1 版中,我们现在可以计算出这个时间(是的,这是使用标准重心天体参考系(BCRS)太阳系全时空坐标系从火星时间转换而来的 "地球时间"):

This is a fairly complicated computation that takes into account not only the motion and rotation of the bodies involved, but also various other physical effects. A more “down to Earth” example that one might readily check by looking out of one’s window is to compute the rise and set times of the Moon from a particular point on the Earth:
这是一项相当复杂的计算,不仅要考虑相关天体的运动和旋转,还要考虑其他各种物理效应。一个更 "接地气 "的例子是,从地球上的某一点计算月球的升起和落下时间:
There’s a slight variation in the times between moonrises:
两次月升之间的时间略有不同:
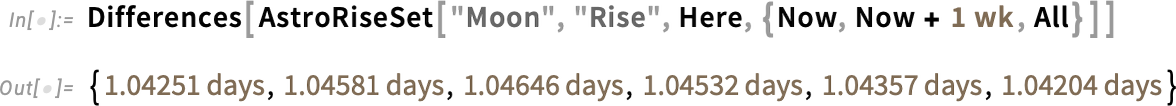
Over the course of a year we see systematic variations associated with the periods of different kinds of lunar months:
在一年中,我们可以看到与不同种类的农历月份的周期有关的系统性变化:

There are all sorts of subtleties here. For example, when exactly does one define something (like the Sun) to have “risen”? Is it when the top of the Sun first peeks out? When the center appears? Or when the “whole Sun” is visible? In Version 14.1 you can ask about any of these:
这里有各种各样的微妙之处。例如,究竟什么时候才算 "太阳升起"?是太阳的顶部第一次露出来的时候?当中心出现时?还是当 "整个太阳 "出现时?在 14.1 版中,您可以询问其中任何一个问题:
Oh, and you could compute the same thing for the rise of Venus, but now to see the differences, you’ve got to go to millisecond granularity (and, by the way, granularities of milliseconds down to picoseconds are new in Version 14.1):
哦,你也可以计算金星上升的时间,但现在要看到差异,你必须使用毫秒粒度(顺便说一下,14.1 版新增了从毫秒到皮秒的粒度):

By the way, particularly for the Sun, the concept of ReferenceAltitude is useful in specifying the various kinds of sunrise and sunset: for example, “civil twilight” corresponds to a reference altitude of –6°.
顺便提一下,特别是对于太阳来说, ReferenceAltitude 的概念在指定各种日出日落时非常有用:例如,"民用黄昏 "对应于-6°的参考高度。
Geometry Goes Color, and Polar
几何、色彩和极地
Last year we introduced the function ARPublish to provide a streamlined way to take 3D geometry and publish it for viewing in augmented reality. In Version 14.1 we’ve now extended this pipeline to deal with color:
去年,我们引入了函数 ARPublish 以提供一种简化的方法来获取 3D 几何图形并将其发布到增强现实中查看。现在,我们在 14.1 版中扩展了这一管道,以处理颜色问题:

(Yes, the color is a little different on the phone because the phone tries to make it look “more natural”.)
(是的,手机上的颜色有点不同,因为手机试图让它看起来 "更自然")。

And now it’s easy to view this not just on a phone, but also, for example, on the Apple Vision Pro:
现在,不仅可以在手机上轻松查看,还可以在 Apple Vision Pro 上查看:
Graphics have always had color. But now in Version 14.1 symbolic geometric regions can have color too:
图形一直都有颜色。但现在在 14.1 版中,符号几何区域也可以有颜色:

And constructive geometric operations on regions preserve color:

Two other new functions in Version 14.1 are PolarCurve and FilledPolarCurve:

And while at this level this may look simple, what’s going on underneath is actually seriously complicated, with all sorts of symbolic analysis needed in order to determine what the “inside” of the parametric curve should be.
Talking about geometry and color brings up another enhancement in Version 14.1: plot themes for diagrams in synthetic geometry. Back in Version 12.0 we introduced symbolic synthetic geometry—in effect finally providing a streamlined computable way to do the kind of geometry that Euclid did two millennia ago. In the past few versions we’ve been steadily expanding our synthetic geometry capabilities, and now in Version 14.1 one notable thing we’ve added is the ability to use plot themes—and explicit graphics options—to style geometric diagrams. Here’s the default version of a geometric diagram:

Now we can “theme” this for the web:

New Computation Flow in Notebooks: Introducing Cell-Linked %
In building up computations in notebooks, one very often finds oneself wanting to take a result one just got and then do something with it. And ever since Version 1.0 one’s been able to do this by referring to the result one just got as %. It’s very convenient. But there are some subtle and sometimes frustrating issues with it, the most important of which has to do with what happens when one reevaluates an input that contains %.
Let’s say you’ve done this:

But now you decide that actually you wanted Median[ % ^ 2 ] instead. So you edit that input and reevaluate it:

Oops! Even though what’s right above your input in the notebook is a list, the value of % is the latest result that was computed, which you can’t now see, but which was 3.
OK, so what can one do about this? We’ve thought about it for a long time (and by “long” I mean decades). And finally now in Version 14.1 we have a solution—that I think is very nice and very convenient. The core of it is a new notebook-oriented analog of %, that lets one refer not just to things like “the last result that was computed” but instead to things like “the result computed in a particular cell in the notebook”.
So let’s look at our sequence from above again. Let’s start typing another cell—say to “try to get it right”. In Version 14.1 as soon as we type % we see an autosuggest menu:

The menu is giving us a choice of (output) cells that we might want to refer to. Let’s pick the last one listed:

The ![]() object is a reference to the output from the cell that’s currently labeled In[1]—and using
object is a reference to the output from the cell that’s currently labeled In[1]—and using ![]() now gives us what we wanted.
now gives us what we wanted.
But let’s say we go back and change the first (input) cell in the notebook—and reevaluate it:

The cell now gets labeled In[5]—and the ![]() (in In[4]) that refers to that cell will immediately change to
(in In[4]) that refers to that cell will immediately change to ![]() :
:

And if we now evaluate this cell, it’ll pick up the value of the output associated with In[5], and give us a new answer:

So what’s really going on here? The key idea is that ![]() signifies a new type of notebook element that’s a kind of cell-linked analog of %. It represents the latest result from evaluating a particular cell, wherever the cell may be, and whatever the cell may be labeled. (The
signifies a new type of notebook element that’s a kind of cell-linked analog of %. It represents the latest result from evaluating a particular cell, wherever the cell may be, and whatever the cell may be labeled. (The ![]() object always shows the current label of the cell it’s linked to.) In effect
object always shows the current label of the cell it’s linked to.) In effect ![]() is “notebook front end oriented”, while ordinary % is kernel oriented.
is “notebook front end oriented”, while ordinary % is kernel oriented. ![]() is linked to the contents of a particular cell in a notebook; % refers to the state of the Wolfram Language kernel at a certain time.
is linked to the contents of a particular cell in a notebook; % refers to the state of the Wolfram Language kernel at a certain time.
![]() gets updated whenever the cell it’s referring to is reevaluated. So its value can change either through the cell being explicitly edited (as in the example above) or because reevaluation gives a different value, say because it involves generating a random number:
gets updated whenever the cell it’s referring to is reevaluated. So its value can change either through the cell being explicitly edited (as in the example above) or because reevaluation gives a different value, say because it involves generating a random number:

OK, so ![]() always refers to “a particular cell”. But what makes a cell a particular cell? It’s defined by a unique ID that’s assigned to every cell. When a new cell is created it’s given a universally unique ID, and it carries that same ID wherever it’s placed and whatever its contents may be (and even across different sessions). If the cell is copied, then the copy gets a new ID. And although you won’t explicitly see cell IDs,
always refers to “a particular cell”. But what makes a cell a particular cell? It’s defined by a unique ID that’s assigned to every cell. When a new cell is created it’s given a universally unique ID, and it carries that same ID wherever it’s placed and whatever its contents may be (and even across different sessions). If the cell is copied, then the copy gets a new ID. And although you won’t explicitly see cell IDs, ![]() works by linking to a cell with a particular ID.
works by linking to a cell with a particular ID.
One can think of ![]() as providing a “more stable” way to refer to outputs in a notebook. And actually, that’s true not just within a single session, but also across sessions. Say one saves the notebook above and opens it in a new session. Here’s what you’ll see:
as providing a “more stable” way to refer to outputs in a notebook. And actually, that’s true not just within a single session, but also across sessions. Say one saves the notebook above and opens it in a new session. Here’s what you’ll see:

The ![]() is now grayed out. So what happens if we try to reevaluate it? Well, we get this:
is now grayed out. So what happens if we try to reevaluate it? Well, we get this:

If we press Reconstruct from output cell the system will take the contents of the first output cell that was saved in the notebook, and use this to get input for the cell we’re evaluating:

In almost all cases the contents of the output cell will be sufficient to allow the expression “behind it” to be reconstructed. But in some cases—like when the original output was too big, and so was elided—there won’t be enough in the output cell to do the reconstruction. And in such cases it’s time to take the Go to input cell branch, which in this case will just take us back to the first cell in the notebook, and let us reevaluate it to recompute the output expression it gives.
By the way, whenever you see a “positional %” you can hover over it to highlight the cell it’s referring to:

Having talked a bit about “cell-linked %” it’s worth pointing out that there are still cases when you’ll want to use “ordinary %”. A typical example is if you have an input line that you’re using a bit like a function (say for post-processing) and that you want to repeatedly reevaluate to see what it produces when applied to your latest output.
In a sense, ordinary % is the “most volatile” in what it refers to. Cell-linked % is “less volatile”. But sometimes you want no volatility at all in what you’re referring to; you basically just want to burn a particular expression into your notebook. And in fact the % autosuggest menu gives you a way to do just that.
Notice the ![]() that appears in whatever row of the menu you’re selecting:
that appears in whatever row of the menu you’re selecting:

Press this and you’ll insert (in iconized form) the whole expression that’s being referred to:

Now—for better or worse—whatever changes you make in the notebook won’t affect the expression, because it’s right there, in literal form, “inside” the icon. And yes, you can explicitly “uniconize” to get back the original expression:

Once you have a cell-linked % it always has a contextual menu with various actions:
一旦有了单元格链接 % ,它总是有一个包含各种操作的上下文菜单:

One of those actions is to do what we just mentioned, and replace the positional ![]() by an iconized version of the expression it’s currently referring to. You can also highlight the output and input cells that the
by an iconized version of the expression it’s currently referring to. You can also highlight the output and input cells that the ![]() is “linked to”. (Incidentally, another way to replace a
is “linked to”. (Incidentally, another way to replace a ![]() by the expression it’s referring to is simply to “evaluate in place”
by the expression it’s referring to is simply to “evaluate in place” ![]() , which you can do by selecting it and pressing CMDReturn or ShiftControlEnter.)
, which you can do by selecting it and pressing CMDReturn or ShiftControlEnter.)
其中一项操作就是执行我们刚才提到的操作,将位置 ![]() 替换为当前引用表达式的图标化版本。您还可以高亮显示
替换为当前引用表达式的图标化版本。您还可以高亮显示 ![]() 所 "链接 "的输出和输入单元格。(顺便提一下,用表达式替换
所 "链接 "的输出和输入单元格。(顺便提一下,用表达式替换 ![]() 的另一种方法是简单地 "就地求值"
的另一种方法是简单地 "就地求值" ![]() ,您可以通过选择 CMD Return 或 Shift Control Enter 来实现)。
,您可以通过选择 CMD Return 或 Shift Control Enter 来实现)。
Another item in the ![]() menu is Replace With Rolled-Up Inputs. What this does is—as it says—to “roll up” a sequence of “
menu is Replace With Rolled-Up Inputs. What this does is—as it says—to “roll up” a sequence of “![]() references” and create a single expression from them:
references” and create a single expression from them:
![]() 菜单中的另一个项目是 Replace With Rolled-Up Inputs 。如其所述,它的作用是 "卷起 "一系列"
菜单中的另一个项目是 Replace With Rolled-Up Inputs 。如其所述,它的作用是 "卷起 "一系列" ![]() 引用",并从中创建一个表达式:
引用",并从中创建一个表达式:

What we’ve talked about so far one can think of as being “normal and customary” uses of ![]() . But there are all sorts of corner cases that can show up. For example, what happens if you have a
. But there are all sorts of corner cases that can show up. For example, what happens if you have a ![]() that refers to a cell you delete? Well, within a single (kernel) session that’s OK, because the expression “behind” the cell is still available in the kernel (unless you reset your $HistoryLength etc.). Still, the
that refers to a cell you delete? Well, within a single (kernel) session that’s OK, because the expression “behind” the cell is still available in the kernel (unless you reset your $HistoryLength etc.). Still, the ![]() will show up with a “red broken link” to indicate that “there could be trouble”:
will show up with a “red broken link” to indicate that “there could be trouble”:
![]()
And indeed if you go to a different (kernel) session there will be trouble—because the information you need to get the expression to which the ![]() refers is simply no longer available, so it has no choice but to show up in a kind of everything-has-fallen-apart “surrender state” as:
refers is simply no longer available, so it has no choice but to show up in a kind of everything-has-fallen-apart “surrender state” as:
事实上,如果您转到另一个(内核)会话,就会遇到麻烦--因为您要获取 ![]() 所指的表达式所需的信息已不再可用,所以它只能以一种万事俱备、只欠东风的 "投降状态 "出现:
所指的表达式所需的信息已不再可用,所以它只能以一种万事俱备、只欠东风的 "投降状态 "出现:
![]()
![]() is primarily useful when it refers to cells in the notebook you’re currently using (and indeed the autosuggest menu will contain only cells from your current notebook). But what if it ends up referring to a cell in a different notebook, say because you copied the cell from one notebook to another? It’s a precarious situation. But if all relevant notebooks are open,
is primarily useful when it refers to cells in the notebook you’re currently using (and indeed the autosuggest menu will contain only cells from your current notebook). But what if it ends up referring to a cell in a different notebook, say because you copied the cell from one notebook to another? It’s a precarious situation. But if all relevant notebooks are open, ![]() can still work, though it’s displayed in purple with an action-at-a-distance “wi-fi icon” to indicate its precariousness:
can still work, though it’s displayed in purple with an action-at-a-distance “wi-fi icon” to indicate its precariousness:
![]() 主要用于指当前使用的笔记本中的单元格(事实上,自动建议菜单将只包含当前笔记本中的单元格)。但是,如果它最终指向的是另一个笔记本中的单元格,例如,由于您将单元格从一个笔记本复制到了另一个笔记本,那该怎么办呢?这种情况很危险。但是,如果所有相关笔记本都已打开,
主要用于指当前使用的笔记本中的单元格(事实上,自动建议菜单将只包含当前笔记本中的单元格)。但是,如果它最终指向的是另一个笔记本中的单元格,例如,由于您将单元格从一个笔记本复制到了另一个笔记本,那该怎么办呢?这种情况很危险。但是,如果所有相关笔记本都已打开, ![]() 仍然可以工作,尽管它会显示为紫色,并带有一个远距离操作的 "wi-fi 图标",以显示其不稳定性:
仍然可以工作,尽管它会显示为紫色,并带有一个远距离操作的 "wi-fi 图标",以显示其不稳定性:
![]()
And if, for example, you start a new session, and the notebook containing the “source” of the ![]() isn’t open, then you’ll get the “surrender state”. (If you open the necessary notebook it’ll “unsurrender” again.)
isn’t open, then you’ll get the “surrender state”. (If you open the necessary notebook it’ll “unsurrender” again.)
例如,如果您开始一个新会话,而包含 ![]() 的 "源代码 "的笔记本没有打开,那么您就会进入 "投降状态"。(如果你打开了必要的笔记本,它就会再次 "取消投降")。
的 "源代码 "的笔记本没有打开,那么您就会进入 "投降状态"。(如果你打开了必要的笔记本,它就会再次 "取消投降")。
Yes, there are lots of tricky cases to cover (in fact, many more than we’ve explicitly discussed here). And indeed seeing all these cases makes us not feel bad about how long it’s taken for us to conceptualize and implement ![]() .
.
是的,有很多棘手的情况需要处理(事实上,比我们在此明确讨论的情况要多得多)。事实上,看到所有这些情况,我们就不会为我们花了如此长的时间来构思和实现 ![]() 而感到遗憾。
而感到遗憾。
The most common way to access ![]() is to use the % autosuggest menu. But if you know you want a
is to use the % autosuggest menu. But if you know you want a ![]() , you can always get it by “pure typing”, using for example ESC%ESC. (And, yes, ESC%%ESC or ESC%5ESC etc. also work, so long as the necessary cells are present in your notebook.)
, you can always get it by “pure typing”, using for example ESC%ESC. (And, yes, ESC%%ESC or ESC%5ESC etc. also work, so long as the necessary cells are present in your notebook.)
访问 ![]() 的最常用方法是使用 % 自动建议菜单。但是,如果您知道自己想要
的最常用方法是使用 % 自动建议菜单。但是,如果您知道自己想要 ![]() ,您可以通过 "纯键入 "来获得,例如使用 ESC % ESC 。(当然,只要笔记本中存在必要的单元格, ESC %% ESC 或 ESC %5 ESC 等也可以使用)。
,您可以通过 "纯键入 "来获得,例如使用 ESC % ESC 。(当然,只要笔记本中存在必要的单元格, ESC %% ESC 或 ESC %5 ESC 等也可以使用)。
The UX Journey Continues: New Typing Affordances, and More
用户体验之旅仍在继续:新的打字功能及其他
We invented Wolfram Notebooks more than 36 years ago, and we’ve been improving and polishing them ever since. And in Version 14.1 we’re implementing several new ideas, particularly around making it even easier to type Wolfram Language code.
我们在 36 年前发明了 Wolfram 笔记本,从那时起我们就一直在改进和完善它。在 14.1 版中,我们将实现一些新的想法,尤其是让 Wolfram 语言代码的输入变得更加容易。
It’s worth saying at the outset that good UX ideas quickly become essentially invisible. They just give you hints about how to interpret something or what to do with it. And if they’re doing their job well, you’ll barely notice them, and everything will just seem “obvious”.
So what’s new in UX for Version 14.1? First, there’s a story around brackets. We first introduced syntax coloring for unmatched brackets back in the late 1990s, and gradually polished it over the following two decades. Then in 2021 we started “automatching” brackets (and other delimiters), so that as soon as you type “f[” you immediately get f[ ].
那么 14.1 版的用户体验有哪些新变化呢?首先是关于括号的故事。早在 20 世纪 90 年代末,我们就首次为不匹配的括号引入了语法着色,并在随后的 20 年中逐步完善。之后在 2021 年,我们开始 "自动匹配 "括号(和其他分隔符),因此只要您输入 "f[",就会立即得到 f[ ] 。
But how do you keep on typing? You could use an ![]() to “move through” the ]. But we’ve set it up so you can just “type through” ] by typing ]. In one of those typical pieces of UX subtlety, however, “type through” doesn’t always make sense. For example, let’s say you typed f[x]. Now you click right after [ and you type g[, so you’ve got f[g[x]. You might think there should be an autotyped ] to go along with the [ after g. But where should it go? Maybe you want to get f[g[x]], or maybe you’re really trying to type f[g[],x]. We definitely don’t want to autotype ] in the wrong place. So the best we can do is not autotype anything at all, and just let you type the ] yourself, where you want it. But remember that with f[x] on its own, the ] is autotyped, and so if you type ] yourself in this case, it’ll just type through the autotyped ] and you won’t explicitly see it.
to “move through” the ]. But we’ve set it up so you can just “type through” ] by typing ]. In one of those typical pieces of UX subtlety, however, “type through” doesn’t always make sense. For example, let’s say you typed f[x]. Now you click right after [ and you type g[, so you’ve got f[g[x]. You might think there should be an autotyped ] to go along with the [ after g. But where should it go? Maybe you want to get f[g[x]], or maybe you’re really trying to type f[g[],x]. We definitely don’t want to autotype ] in the wrong place. So the best we can do is not autotype anything at all, and just let you type the ] yourself, where you want it. But remember that with f[x] on its own, the ] is autotyped, and so if you type ] yourself in this case, it’ll just type through the autotyped ] and you won’t explicitly see it.
但如何继续键入呢?您可以使用 ![]() 来 "穿过" ] 。但是我们已经设置好,您只需键入 ] 即可 "键入" ] 。然而,在用户体验的典型微妙之处中,"键入通过 "并不总是有意义的。例如,假设您键入了 f[x] 。现在,您点击 [ 之后的右键,然后键入 g[ ,这样您就得到了 f[g[x] 。您可能会认为,在 g 之后,应该有一个自动生成的 ] 与 [ 搭配使用。但是它应该放在哪里呢?也许您想输入 f[g[x]] ,也许您真的想输入 f[g[],x] 。我们肯定不想在错误的地方自动键入 ] 。因此,我们能做的最好的办法就是不自动键入任何内容,而是让您自己键入 ] 到您想要的位置。但是请记住,在 f[x] 独立存在的情况下, ] 是自动键入的,因此在这种情况下,如果您自己键入 ] ,它只会通过自动键入的 ] 键入,您不会明确看到它。
来 "穿过" ] 。但是我们已经设置好,您只需键入 ] 即可 "键入" ] 。然而,在用户体验的典型微妙之处中,"键入通过 "并不总是有意义的。例如,假设您键入了 f[x] 。现在,您点击 [ 之后的右键,然后键入 g[ ,这样您就得到了 f[g[x] 。您可能会认为,在 g 之后,应该有一个自动生成的 ] 与 [ 搭配使用。但是它应该放在哪里呢?也许您想输入 f[g[x]] ,也许您真的想输入 f[g[],x] 。我们肯定不想在错误的地方自动键入 ] 。因此,我们能做的最好的办法就是不自动键入任何内容,而是让您自己键入 ] 到您想要的位置。但是请记住,在 f[x] 独立存在的情况下, ] 是自动键入的,因此在这种情况下,如果您自己键入 ] ,它只会通过自动键入的 ] 键入,您不会明确看到它。
So how can you tell whether a ] you type will explicitly show up, or will just be “absorbed” as type-through? In Version 14.1 there’s now different syntax coloring for these cases: yellow if it’ll be “absorbed”, and pink if it’ll explicitly show up.
那么,如何判断您键入的 ]是会明确显示出来,还是会被 "吸收 "为穿透型呢?在 14.1 版中,针对这些情况有了不同的语法着色:如果会被 "吸收",则为黄色;如果会明确显示,则为粉色。
This is an example of non-type-through, so Range is colored yellow and the ] you type is “absorbed”:
这是一个非穿透类型的示例,因此 Range 被染成黄色,而您键入的 ] 则被 "吸收":

And this is an example of non-type-through, so Round is colored pink and the ] you type is explicitly inserted:
这是一个非穿透类型的示例,因此 Round 会被染成粉红色,而您键入的 ] 会被明确插入:
![]()
This may all sound very fiddly and detailed—and for us in developing it, it is. But the point is that you don’t explicitly have to think about it. You quickly learn to just “take the hint” from the syntax coloring about when your closing delimiters will be “absorbed” and when they won’t. And the result is that you’ll have an even smoother and faster typing experience, with even less chance of unmatched (or incorrectly matched) delimiters.
这一切听起来可能非常繁琐和细致,而对于我们开发人员来说,确实如此。但问题是,你不需要明确地考虑这一点。你很快就能从语法着色中学会 "接受暗示",知道什么时候你的结尾分隔符会被 "吸收",什么时候不会被 "吸收"。结果就是,你将获得更流畅、更快速的键入体验,更少出现分隔符不匹配(或错误匹配)的情况。
The new syntax coloring we just discussed helps in typing code. In Version 14.1 there’s also something new that helps in reading code. It’s an enhanced version of something that’s actually common in IDEs: when you click (or select) a variable, every instance of that variable immediately gets highlighted:
我们刚刚讨论过的新语法着色有助于键入代码。在 14.1 版中,还有一些新功能有助于阅读代码。它是集成开发环境中常见功能的增强版:当您单击(或选择)一个变量时,该变量的每个实例都会立即高亮显示:

What’s subtle in our case is that we take account of the scoping of localized variables—putting a more colorful highlight on instances of a variable that are in scope:
在我们的例子中,最微妙的是我们考虑到了本地化变量的作用域--为处于作用域内的变量实例添加了更多色彩:

One place this tends to be particularly useful is in understanding nested pure functions that use #. By clicking a # you can see which other instances of # are in the same pure function, and which are in different ones (the highlight is bluer inside the same function, and grayer outside):
在理解使用 # 的嵌套纯函数时,这一点往往特别有用。通过点击 # 可以查看 # 的其他实例中哪些在同一个纯函数中,哪些在不同的纯函数中(同一函数内部的高亮度更蓝,外部的高亮度更灰):
![]()
On the subject of finding variables, another change in Version 14.1 is that fuzzy name autocompletion now also works for contexts. So if you have a symbol whose full name is context1`subx`var2 you can type c1x and you’ll get a completion for the context; then accept this and you get a completion for the symbol.
关于查找变量,14.1 版的另一个变化是模糊名称自动完成功能现在也适用于上下文。因此,如果一个符号的全名是 context1`subx`var2 ,你可以输入 c1x ,就会得到上下文的补全;然后接受它,就会得到符号的补全。
There are also several other notable UX “tune-ups” in Version 14.1. For many years, there’s been an “information box” that comes up whenever you hover over a symbol. Now that’s been extended to entities—so (alongside their explicit form) you can immediately get to information about them and their properties:
14.1 版还对用户体验进行了其他一些显著的 "调整"。多年来,只要将鼠标悬停在符号上,就会出现一个 "信息框"。现在,该功能已扩展到实体,因此(除了实体的显式形式外),您还可以立即获取有关实体及其属性的信息:
![]()
Next there’s something that, yes, I personally have found frustrating in the past. Say you’ve a file, or an image, or something else somewhere on your computer’s desktop. Normally if you want it in a Wolfram Notebook you can just drag it there, and it will very beautifully appear. But what if the thing you’re dragging is very big, or has some other kind of issue? In the past, the drag just failed. Now what happens is that you get the explicit Import that the dragging would have done, so that you can run it yourself (getting progress information, etc.), or you can modify it, say adding relevant options.
接下来还有一件事,是的,我个人在过去也曾感到沮丧。比方说,你在电脑桌面上有一个文件、一张图片或其他东西。通常情况下,如果你想把它放到 Wolfram 笔记本中,只需将它拖到那里,它就会非常漂亮地显示出来。但如果您拖动的东西非常大或有其他问题怎么办?过去,拖动会失败。现在,您将获得拖动本应完成的显式 Import ,这样您就可以自己运行它(获得进度信息等),或者对它进行修改,例如添加相关选项。
Another small piece of polish that’s been added in Version 14.1 has to do with Preferences. There are a lot of things you can set in the notebook front end. And they’re explained, at least briefly, in the many Preferences panels. But in Version 14.1 there are now (i) buttons that give direct links to the relevant workflow documentation:
14.1 版中添加的另一小部分改进与 Preferences 有关。您可以在笔记本前端设置很多内容。在许多 Preferences 面板中都有简要说明。但在 14.1 版中, (i) 按钮提供了相关工作流文档的直接链接:

Syntax for Natural Language Input
自然语言输入语法
Ever since shortly after Wolfram|Alpha was released in 2009, there’ve been ways to access its natural language understanding capabilities in the Wolfram Language. Foremost among these has been CTRL=—which lets you type free-form natural language and immediately get a Wolfram Language version, often in terms of entities, etc.:
自 2009 年Wolfram|Alpha发布后不久,就有很多方法可以访问 Wolfram 语言中的自然语言理解功能。其中最重要的是 CTRL = - 您可以输入自由格式的自然语言,并立即获得 Wolfram 语言的版本,通常是实体等方面的版本:
![]()
Generally this is a very convenient and elegant capability. But sometimes one may want to just use plain text to specify natural language input, for example so that one doesn’t interrupt one’s textual typing of input.
一般来说,这是一种非常方便和优雅的功能。但有时,人们可能只想使用纯文本来指定自然语言输入,例如,这样就不会中断文本输入。
In Version 14.1 there’s a new mechanism for this: syntax for directly entering free-form natural language input. The syntax is a kind of a “textified” version of CTRL=: =[…]. When you type =[...] as input nothing immediately happens. It’s only when you evaluate your input that the natural language gets interpreted—and then whatever it specifies is computed.
14.1 版为此提供了一种新机制:直接输入自由格式自然语言输入的语法。该语法是 CTRL = 的 "文本化 "版本: =[…] 。当您输入 =[...] 时,什么也不会立即发生。只有当您对输入进行评估时,自然语言才会被解释,然后它指定的任何内容才会被计算。
Here’s a very simple example, where each =[…] just turns into an entity:
下面是一个非常简单的例子,每个 =[…] 都会变成一个实体:

But when the result of interpreting the natural language is an expression that can be further evaluated, what will come out is the result of that evaluation:
但是,当解释自然语言的结果是一个可以进一步评估的表达式时,出来的就是评估的结果:

One feature of using =[…] instead of CTRL= is that =[…] is something anyone can immediately see how to type:
使用 =[…] 而不是 CTRL = 的一个特点是, =[…] 任何人都能一眼看出如何键入:
But what actually is =[…]? Well, it’s just input syntax for the new function FreeformEvaluate:
但 =[…] 究竟是什么呢?它只是新函数 FreeformEvaluate 的输入语法:

You can use FreeformEvaluate inside a program—here, rather whimsically, to see what interpretations are chosen by default for “a” followed by each letter of the alphabet:
您可以在程序中使用 FreeformEvaluate --在这里,您可以异想天开地查看默认情况下,字母表中每个字母后面的 "a "会选择什么解释:
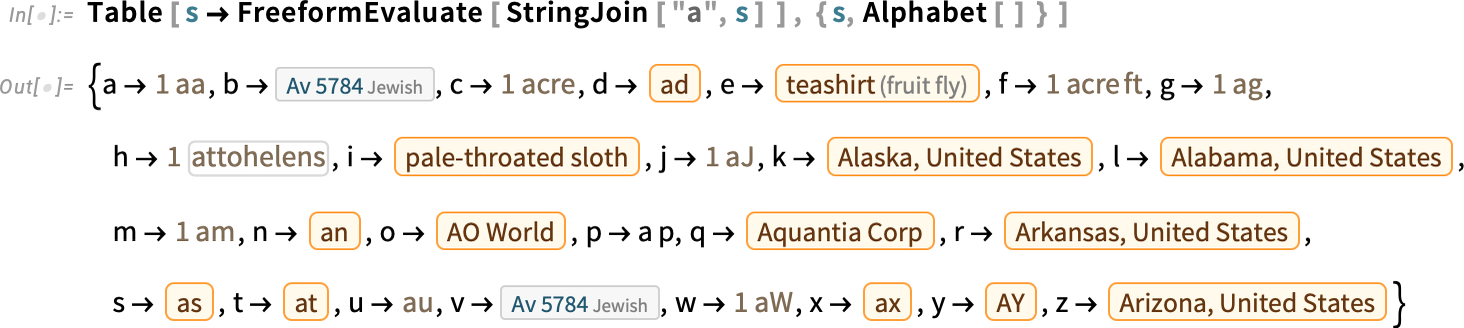
By default, FreeformEvaluate interprets your input, then evaluates it. But you can also specify that you want to hold the result of the interpretation:
默认情况下, FreeformEvaluate 会解释输入内容,然后对其进行求值。但您也可以指定保留解释的结果:

Diff[ ] … for Notebooks and More!
Diff[ ] ...用于笔记本及其他产品!
It’s been a very long-requested capability: give me a way to tell what changed, particularly in a notebook. It’s fairly easy to do “diffs” for plain text. But for notebooks—as structured symbolic documents—it’s a much more complicated story. But in Version 14.1 it’s here! We’ve got a function Diff for doing diffs in notebooks, and actually also in many other kinds of things.
这是一项长期以来一直被要求的功能:让我有办法知道哪些内容发生了变化,尤其是在笔记本中。对纯文本进行 "差异 "处理相当容易。但对于作为结构化符号文档的笔记本来说,情况就要复杂得多。不过,在 14.1 版中就有了!我们已经有了一个函数 Diff 用于在笔记本中进行差异处理,实际上也可以在许多其他类型的东西中进行差异处理。
Here’s an example, where we’re requesting a “side-by-side view” of the diff between two notebooks:
下面是一个例子,我们要求 "并排查看 "两个笔记本之间的差异:

And here’s an “alignment chart view” of the diff:
这是差分的 "排列图视图":

Like everything else in the Wolfram Language, a “diff” is a symbolic expression. Here’s an example:
与 Wolfram 语言中的其他内容一样,"diff "也是一种符号表达式。下面是一个例子:

There are lots of different ways to display a diff object; many of them one can select interactively with the menu:
有许多不同的方法来显示不同的对象;其中许多方法可以通过菜单进行交互式选择:

But the most important thing about diff objects is that they can be used programmatically. And in particular DiffApply applies the diffs from a diff object to an existing object, say a notebook.
不过,diff 对象最重要的一点是,它们可以编程使用。尤其是 DiffApply 可以将 diff 对象中的差异应用到现有对象(例如笔记本)中。
What’s the point of this? Well, let’s imagine you’ve made a notebook, and given a copy of it to someone else. Then both you and the person to whom you’ve given the copy make changes. You can create a diff object of the diffs between the original version of the notebook, and the version with your changes. And if the changes the other person made don’t overlap with yours, you can just take your diffs and use DiffApply to apply your diffs to their version, thereby getting a “merged notebook” with both sets of changes made.
这有什么意义呢?假设你做了一本笔记本,并把它的副本给了别人。然后,你和被你复制的人都做了修改。你可以创建一个 diff 对象,显示笔记本的原始版本和你修改后的版本之间的差异。如果其他人所做的改动与你的改动不重叠,你可以直接使用你的差异对象,并使用 DiffApply 将你的差异对象应用到他们的版本中,从而得到一个包含两组改动的 "合并笔记本"。
But what if your changes might conflict? Well, then you need to use the function Diff3. Diff3 takes your original notebook and two modified versions, and does a “three-way diff” to give you a diff object in which any conflicts are explicitly identified. (And, yes, three-way diffs are familiar from source control systems in which they provide the back end for making the merging of files as automated as possible.)
但如果您的更改可能会发生冲突怎么办?那么,你需要使用函数 Diff3 。 Diff3 使用你的原始笔记本和两个修改过的版本,并进行 "三向差分",给你一个差分对象,其中任何冲突都会被明确识别出来。(没错,三向差异在源代码控制系统中并不陌生,它为尽可能自动化地合并文件提供了后端)。
Notebooks are an important use case for Diff and related functions. But they’re not the only one. Diff can perfectly well be applied, for example, just to lists:
笔记本是 Diff 和相关功能的一个重要用例。但它们并不是唯一的用例。例如, Diff 完全可以只用于列表:
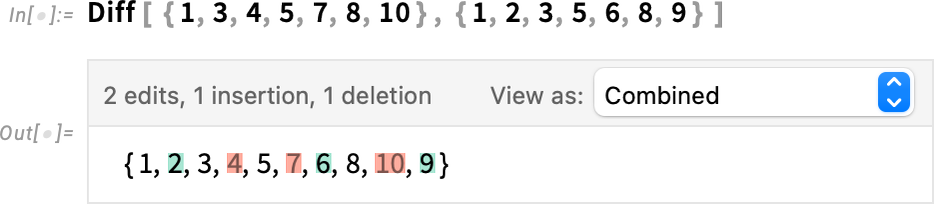
There are many ways to display this diff object; here’s a side-by-side view:
有很多方法可以显示这个差异对象;下面是一个并排视图:

And here’s a “unified view” reminiscent of how one might display diffs for lines of text in a file:
这是一个 "统一视图",让人想起如何显示文件中文本行的差异:

And, speaking of files, Diff, etc. can immediately be applied to files:
说到文件, Diff 等可以立即应用于文件:
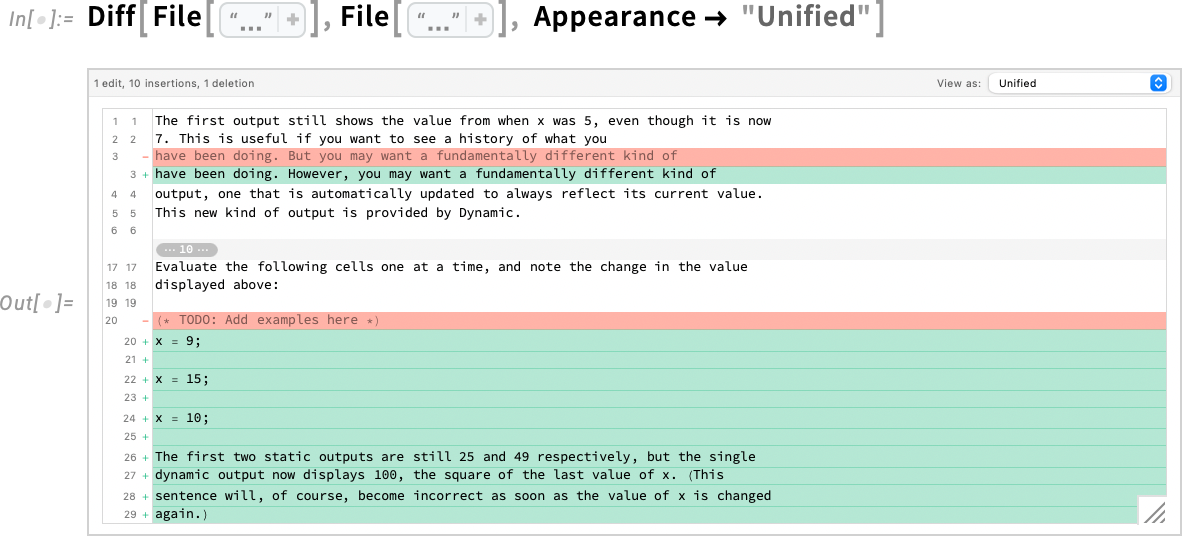
Diff, etc. can also be applied to cells, where they can analyze changes in both content and styles or metadata. Here we’re creating two cells and then diffing them—showing the result in a side by side:
Diff 等也可以应用于单元格,它们可以分析内容、样式或元数据的变化。在这里,我们创建了两个单元格,然后对它们进行了差分--以并列方式显示结果:

In “Combined” view the “pure insertions” are highlighted in green, the “pure deletions” in red, and the “edits” are shown as deletion/insertion stacks:
在 "组合 "视图中,"纯插入 "显示为绿色,"纯删除 "显示为红色,"编辑 "显示为删除/插入堆叠:

Many uses of diff technology revolve around content development—editing, software engineering, etc. But in the Wolfram Language Diff, etc. are set up also to be convenient for information visualization and for various kinds of algorithmic operations. For example, to see what letters differ between the Spanish and Polish alphabets, we can just use Diff:
差分技术的许多用途都围绕着内容开发--编辑、软件工程等。但在 Wolfram 语言中, Diff 等的设置也便于信息可视化和各种算法操作。例如,要查看西班牙语字母表和波兰语字母表中哪些字母不同,我们只需使用 Diff :

Here’s the “pure visualization”:
这里是 "纯可视化":
And here’s an alternate “unified summary” form:
下面是另一种 "统一摘要 "形式:

Another use case for Diff is bioinformatics. We retrieve two genome sequences—as strings—then use Diff:
Diff 的另一个用例是生物信息学。我们以字符串的形式检索两个基因组序列,然后使用 Diff :
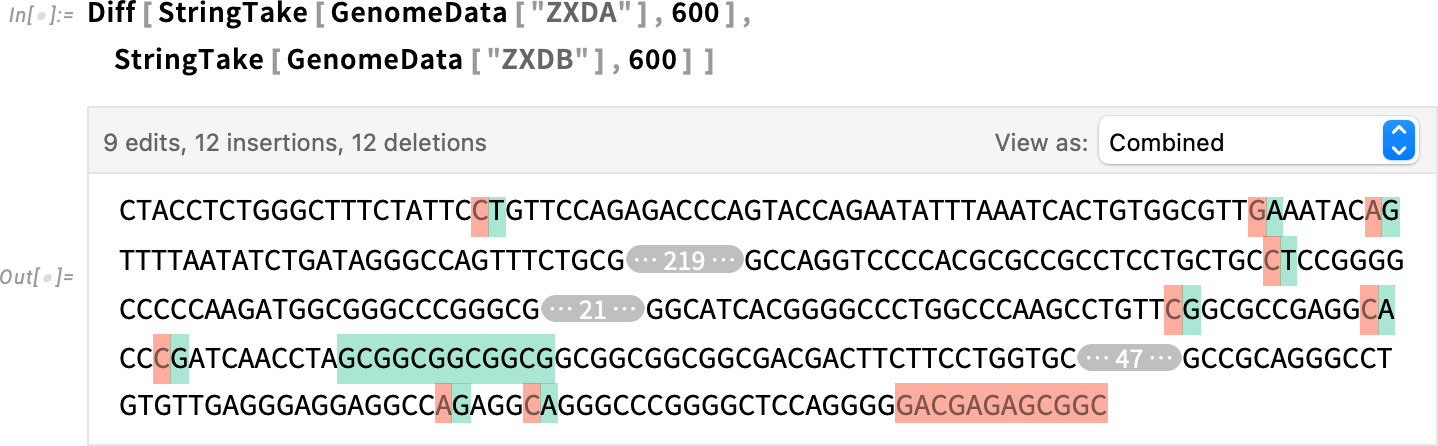
We can take the resulting diff object and show it in a different form—here character alignment:
我们可以将得到的差异对象以不同的形式显示出来--这里是字符对齐:
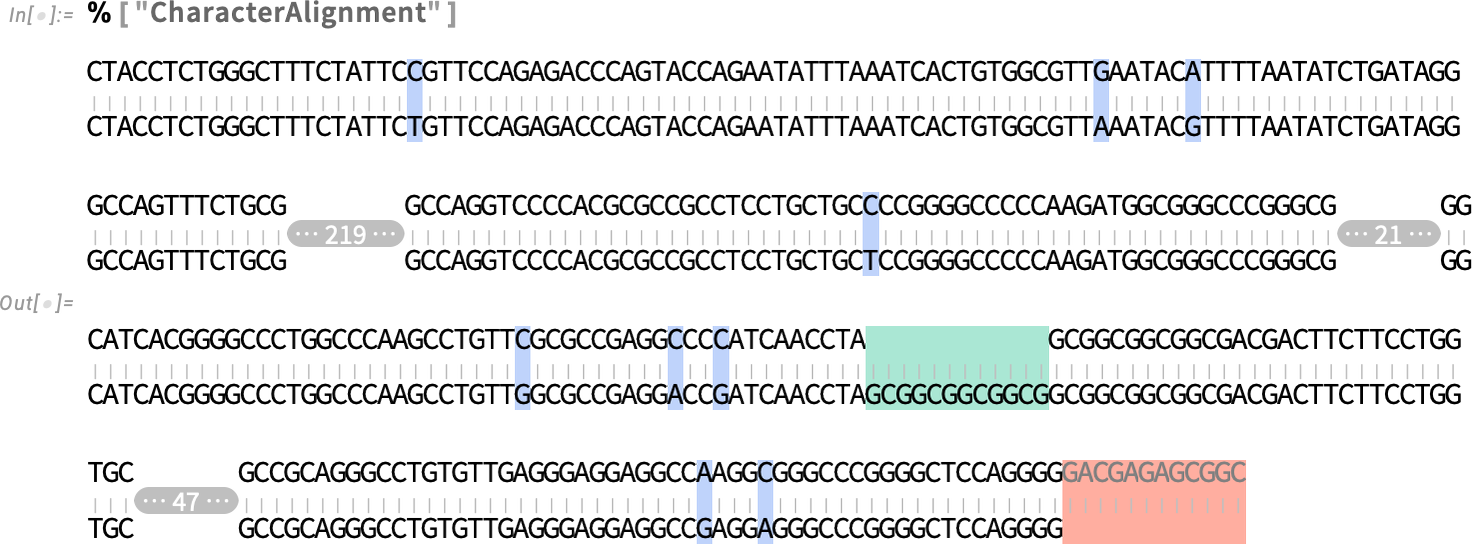
Under the hood, by the way, Diff is finding the differences using SequenceAlignment. But while Diff is giving a “high-level symbolic diff object”, SequenceAlignment is giving a direct low-level representation of the sequence alignment:
顺便说一下,在引擎盖下, Diff 正在使用 SequenceAlignment 查找差异。但是, Diff 给出的是 "高级符号差异对象",而 SequenceAlignment 给出的是序列比对的直接低级表示:

Information visualization isn’t restricted to two-way diffs; here’s an example with a three-way diff:
信息可视化并不局限于双向差异,下面是一个三向差异的例子:

And here it is as a “unified summary”:
这里是 "统一摘要":

There are all sorts of options for diffs. One that is sometimes important is DiffGranularity. By default the granularity for diffs of strings is "Characters":
有各种各样的差异选项。其中一个有时很重要的选项是 DiffGranularity 。默认情况下,字符串差异的粒度是 "Characters" :

But it’s also possible to set it to be "Words":
但也可以将其设置为 "Words" :

Coming back to notebooks, the most “interactive” form of diff is a “report”:
回到笔记本,最 "互动 "的 diff 形式是 "报告":
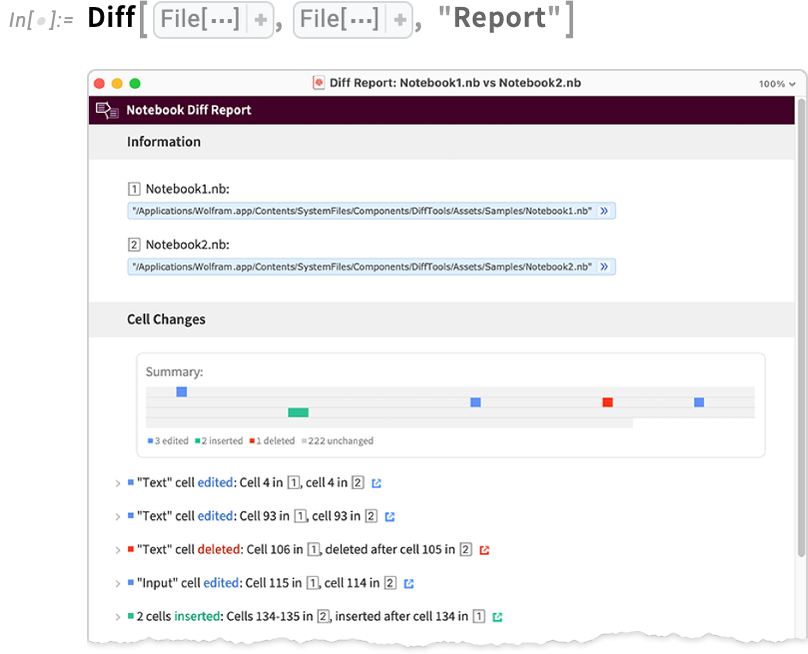
In such a report, you can open cells to see the details of a specific change, and you can also click to jump to where the change occurred in the underlying notebooks.
在这样的报告中,你可以打开单元格查看特定更改的详细信息,还可以单击跳转到底层笔记本中发生更改的位置。
When it comes to analyzing notebooks, there’s another new feature in Version 14.1: NotebookCellData. NotebookCellData gives you direct programmatic access to lots of properties of notebooks. By default it generates a dataset of some of them, here for the notebook in which I’m currently authoring this:
说到分析笔记本,14.1 版中还有一项新功能: NotebookCellData 。 NotebookCellData 可以让你以编程方式直接访问笔记本的大量属性。默认情况下,它会生成其中一些属性的数据集,这里是我正在撰写的笔记本的数据集:
There are properties like the word count in each cell, the style of each cell, the memory footprint of each cell, and a thumbnail image of each cell.
这些属性包括每个单元格的字数、每个单元格的样式、每个单元格的内存占用以及每个单元格的缩略图。
Ever since Version 6 in 2007 we’ve had the CellChangeTimes option which records when cells in notebooks are created or modified. And now in Version 14.1 NotebookCellData provides direct programmatic access to this data. So, for example, here’s a date histogram of when the cells in the current notebook were last changed:
自 2007 年 Version 6 以来,我们一直使用 CellChangeTimes 选项来记录创建或修改笔记本单元格的时间。现在,在 14.1 版中, NotebookCellData 提供了对这些数据的直接编程访问。因此,举例来说,这里有一个日期柱状图,显示了当前笔记本中单元格的最后修改时间:
Lots of Little Language Tune-Ups
大量的语言小调整
It’s part of a journey of almost four decades. Steadily discovering—and inventing—new “lumps of computational work” that make sense to implement as functions or features in the Wolfram Language. The Wolfram Language is of course very much strong enough that one can build essentially any functionality from the primitives that already exist in it. But part of the point of the language is to define the best “elements of computational thought”. And particularly as the language progresses, there’s a continual stream of new opportunities for convenient elements that get exposed. And in Version 14.1 we’ve implemented quite a diverse collection of them.
这是我近四十年历程的一部分。我们不断发现和发明新的 "计算工作",并将其作为 Wolfram 语言的函数或功能加以实现。当然,Wolfram 语言已经足够强大,人们基本上可以利用其中已有的基元构建任何功能。但沃尔夫拉姆语言的部分意义在于定义最佳的 "计算思维元素"。尤其是随着语言的发展,会不断有新的便捷元素出现。在 14.1 版本中,我们已经实现了相当多样化的元素集合。
Let’s say you want to nestedly compose a function. Ever since Version 1.0 there’s been Nest for that:
比方说,您想嵌套地组成一个函数。自1.0版开始,就有了 Nest :
But what if you want the abstract nested function, not yet applied to anything? Well, in Version 14.1 there’s now an operator form of Nest (and NestList) that represents an abstract nested function that can, for example, be composed with other functions, as in
但是,如果您想要尚未应用于任何对象的抽象嵌套函数,该怎么办呢?那么,在 14.1 版中,现在有了 Nest (和 NestList )的运算符形式,可以表示抽象嵌套函数,例如,可以与其他函数组成,如
or equivalently: 或等同于
A decade ago we introduced functions like AllTrue and AnyTrue that effectively “in one gulp” do a whole collection of separate tests. If one wanted to test whether there are any primes in a list, one can always do:
十年前,我们引入了 AllTrue 和 AnyTrue 等函数,这些函数可以 "一气呵成 "地完成一系列单独的测试。如果要测试一个列表中是否存在素数,我们可以这样做:
But it’s better to “package” this “lump of computational work” into the single function AnyTrue:
不过,最好还是把这 "一大堆计算工作""打包 "到单个函数 AnyTrue 中:
In Version 14.1 we’re extending this idea by introducing AllMatch, AnyMatch and NoneMatch:
在 14.1 版中,我们通过引入 AllMatch 、 AnyMatch 和 NoneMatch 扩展了这一想法:
Another somewhat related new function is AllSameBy. SameQ tests whether a collection of expressions are immediately the same. AllSameBy tests whether expressions are the same by the criterion that the value of some function applied to them is the same:
另一个有点相关的新函数是 AllSameBy 。 SameQ 测试表达式集合是否立即相同。 AllSameBy 测试表达式是否相同的标准是,应用于表达式的某个函数的值是否相同:
Talking of tests, another new feature in Version 14.1 is a second argument to QuantityQ (and KnownUnitQ), which lets you test not only whether something is a quantity, but also whether it’s a specific type of physical quantity:
说到测试,14.1 版的另一个新功能是为 QuantityQ (和 KnownUnitQ )添加了第二个参数,这样您不仅可以测试某物是否是量,还可以测试它是否是特定类型的物理量:

And now talking about “rounding things out”, Version 14.1 does that in a very literal way by enhancing the RoundingRadius option. For a start, you can now specify a different rounding radius for particular corners:
说到 "四舍五入",14.1 版通过增强 RoundingRadius 选项,以非常直观的方式做到了这一点。首先,您现在可以为特定的边角指定不同的圆角半径:

And, yes, that’s useful if you’re trying to fit button-like constructs together:
是的,如果你想把类似纽扣的结构组合在一起,这很有用:

By the way, RoundingRadius now also works for rectangles inside Graphics:
顺便提一下, RoundingRadius 现在也适用于 Graphics 内的矩形:
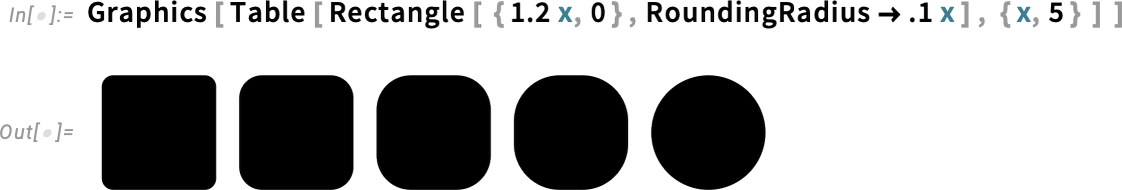
Let’s say you have a string, like “hello”. There are many functions that operate directly on strings. But sometimes you really just want to use a function that operates on lists—and apply it to the characters in a string. Now in Version 14.1 you can do this using StringApply:
比方说,你有一个字符串,比如 "hello"。有很多函数可以直接对字符串进行操作。但有时您真的只想使用一个对列表进行操作的函数,并将其应用于字符串中的字符。现在,在 14.1 版中,您可以使用 StringApply 实现这一功能:
Another little convenience in Version 14.1 is the function BitFlip, which, yes, flips a bit in the binary representation of a number:
14.1 版的另一个小便利是函数 BitFlip ,没错,它可以在数字的二进制表示中翻转一位:
When it comes to Boolean functions, a detail that’s been improved in Version 14.1 is the conversion to NAND representation. By default, functions like BooleanConvert have allowed Nand[p] (which is equivalent to Not[p]). But in Version 14.1 there’s now "BinaryNAND" which yields for example Nand[p, p] instead of just Nand[p] (i.e. Not[p]). So here’s a representation of Or in terms of Nand:
说到布尔函数,14.1 版中改进的一个细节是转换为 NAND 表示法。默认情况下,像 BooleanConvert 这样的函数允许 Nand [p] (相当于 Not [p] )。但在 14.1 版中,现在有了 "BinaryNAND" ,这就产生了例如 Nand [p, p] 而不仅仅是 Nand [p] (即 Not [p] )。因此,这里用 Nand 表示 Or :
Making the Wolfram Compiler Easier to Use
让 Wolfram 编译器更易于使用
Let’s say you have a piece of Wolfram Language code that you know you’re going to run a zillion times—so you want it to run absolutely as fast as possible. Well, you’ll want to make sure you’re doing the best algorithmic things you can (and making the best possible use of Wolfram Language superfunctions, etc.). And perhaps you’ll find it helpful to use things like DataStructure constructs. But ultimately if you really want your code to run absolutely as fast as your computer can make it, you’ll probably want to set it up so that it can be compiled using the Wolfram Compiler, directly to LLVM code and then machine code.
假设您有一段 Wolfram 语言代码,您知道要运行无数次,因此希望它运行得越快越好。那么,您就需要确保自己在算法上做到最好(并尽可能充分利用 Wolfram 语言的超级函数等)。也许您还会发现使用 DataStructure 结构之类的东西很有帮助。但最终,如果您真的希望您的代码以计算机能达到的最快速度运行,您可能会希望对代码进行设置,以便使用Wolfram编译器直接编译为LLVM代码,然后再编译为机器代码。
We’ve been developing the Wolfram Compiler for many years, and it’s becoming steadily more capable (and efficient). And for example it’s become increasingly important in our own internal development efforts. In the past, when we wrote critical inner-loop internal code for the Wolfram Language, we did it in C. But in the past few years we’ve almost completely transitioned instead to writing pure Wolfram Language code that we then compile with the Wolfram Compiler. And the result of this has been a dramatically faster and more reliable development pipeline for writing inner-loop code.
多年来,我们一直在开发 Wolfram 编译器,它的功能和效率正在稳步提高。例如,它在我们自己的内部开发工作中变得越来越重要。过去,当我们为 Wolfram 语言编写关键的内循环内部代码时,我们使用的是 C 语言。但在过去几年中,我们几乎完全过渡到编写纯 Wolfram 语言代码,然后使用 Wolfram 编译器进行编译。这样做的结果是,在编写内循环代码时,开发管道的速度大大加快,而且更加可靠。
Ultimately what the Wolfram Compiler needs to do is to take the code you write and align it with the low-level capabilities of your computer, figuring out what low-level data types can be used for what, etc. Some of this can be done automatically (using all sorts of fancy symbolic and theorem-proving-like techniques). But some needs to be based on collaboration between the programmer and the compiler. And in Version 14.1 we’re adding several important ways to enhance that collaboration.
最终,Wolfram 编译器需要做的是将您编写的代码与计算机的底层功能相匹配,找出哪些底层数据类型可用于哪些用途,等等。其中有些工作可以自动完成(使用各种花哨的符号和类似定理推导的技术)。但也有一部分需要程序员和编译器共同协作完成。在 14.1 版中,我们增加了几种重要的方法来加强这种协作。
The first thing is that it’s now easy to get access to information the compiler has. For example, here’s the type declaration the compiler has for the built-in function Dimensions:
首先,现在可以轻松获取编译器掌握的信息。例如,下面是编译器掌握的内置函数 Dimensions 的类型声明:

And here’s the source code of the actual implementation the compiler is using for Dimensions, calling its intrinsic low-level internal functions like CopyTo:
下面是编译器为 Dimensions 调用其固有的低级内部函数(如 CopyTo )的实际实现的源代码:

A function like Map has a vastly more complex set of type declarations:
像 Map 这样的函数,其类型声明要复杂得多:

For types themselves, CompilerInformation lets you see their type hierarchy:
对于类型本身, CompilerInformation 可以让你看到它们的类型层次结构:
And for data structure types, you can do things like see the fields they contain, and the operations they support:
对于数据结构类型,你可以查看它们包含的字段以及支持的操作:

And, by the way, something new in Version 14.1 is the function OperationDeclaration which lets you declare operations to add to a data structure type you’ve defined.
顺便提一下,14.1 版还新增了 OperationDeclaration 函数,通过该函数,您可以声明要添加到已定义的数据结构类型中的操作。
Once you actually start running the compiler, a convenient new feature in Version 14.1 is a detailed progress monitor that lets you see what the compiler is doing at each step:
一旦开始实际运行编译器,14.1 版的一个便捷新功能是详细的进度监控器,可让您查看编译器在每一步的运行情况:
As we said, the key to compilation is figuring out how to align your code with the low-level capabilities of your computer. The Wolfram Language can do arbitrary symbolic operations. But many of those don’t align with low-level capabilities of your computer, and can’t meaningfully be compiled. Sometimes those failures to align are the result of sophistication that’s possible only with symbolic operations. But sometimes the failures can be avoided if you “unpack” things a bit. And sometimes the failures are just the result of programming mistakes. And now in Version 14.1 the Wolfram Compiler is starting to be able to annotate your code to show where the misalignments are happening, so you can go through and figure out what to do with them. (It’s something that’s uniquely possible because of the symbolic structure of the Wolfram Language and even more so of Wolfram Notebooks.)
正如我们所说,编译的关键在于如何使代码与计算机的底层功能保持一致。Wolfram 语言可以进行任意的符号运算。但其中许多操作并不符合计算机的底层能力,因此无法进行有意义的编译。有时,这些不一致是由于只有符号运算才能实现的复杂性造成的。但有时,如果你稍微 "解包 "一下,就能避免这些故障。有时,失败只是编程错误的结果。现在,在 14.1 版中,Wolfram 编译器开始能够注释您的代码,以显示发生错位的位置,这样您就可以查看并找出如何处理它们。(由于 Wolfram 语言的符号结构,以及 Wolfram 笔记本的独特功能,这一切都成为可能)。
Here’s a very simple example:
这里有一个非常简单的例子:

In compiled code, Sin expects a numerical argument, so a Boolean argument won’t work. Clicking the Source button lets you see where specifically something went wrong:
在编译后的代码中, Sin 希望使用数字参数,因此布尔参数将不起作用。单击 Source 按钮,您就可以看到具体是哪里出错了:

If you have several levels of definitions, the Source button will show you the whole chain:
如果您有多个级别的定义, Source 按钮将显示整个链:

Here’s a slightly more complicated piece of code, in which the specific place where there’s a problem is highlighted:
下面是一段稍微复杂的代码,其中突出显示了出现问题的具体位置:

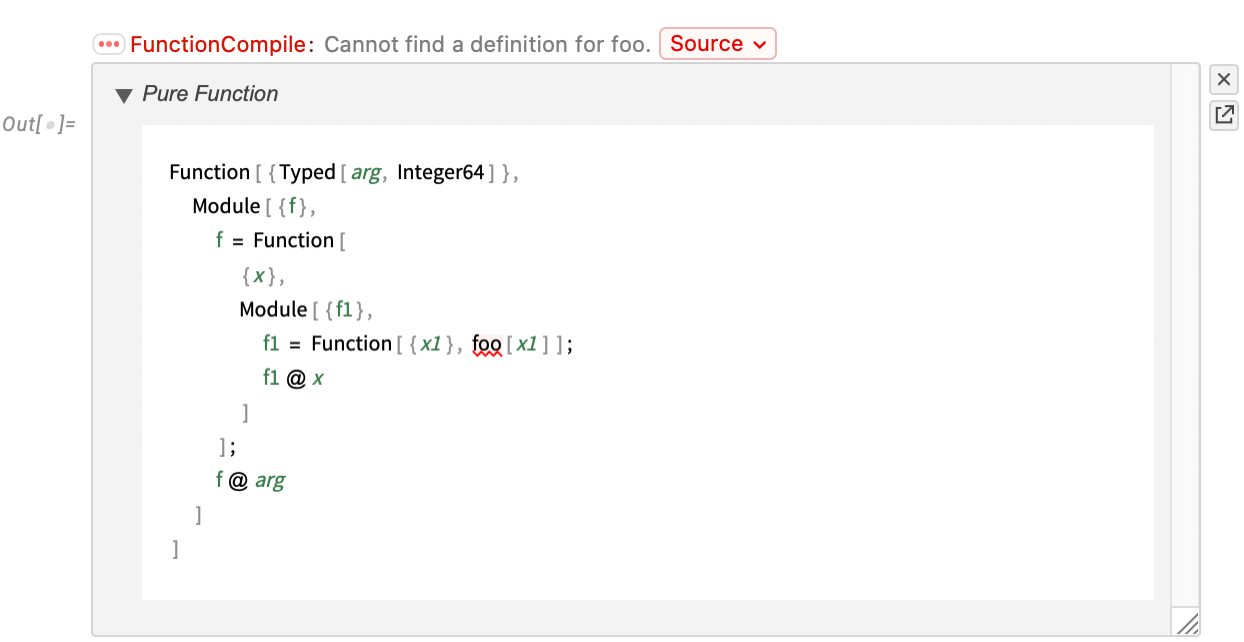
In a typical workflow you might start from pure Wolfram Language code, without Typed and other compilation information. Then you start adding such information, repeatedly trying the compilation, seeing what issues arise, and fixing them. And, by the way, because it’s completely efficient to call small pieces of compiled code within ordinary Wolfram Language code, it’s common to start by annotating and compiling the “innermost inner loops” in your code, and gradually “working outwards”.
在一个典型的工作流程中,您可能会从纯粹的 Wolfram 语言代码开始,没有 Typed 和其他编译信息。然后,您开始添加此类信息,反复尝试编译,查看出现了哪些问题,并加以解决。顺便提一下,由于在普通 Wolfram 语言代码中调用小段编译后的代码是完全高效的,因此通常会从注释和编译代码中的 "最内层内部循环 "开始,然后逐步 "向外扩展"。
But, OK, let’s say you’ve successfully compiled a piece of code. Most of the time it’ll handle certain cases, but not others (for example, it might work fine with machine-precision numbers, but not be capable of handling arbitrary precision). By default, compiled code that’s running is set up to generate a message and revert to ordinary Wolfram Language evaluation if it can’t handle something:
但是,好吧,假设你已经成功编译了一段代码。大多数情况下,它能处理某些情况,但不能处理其他情况(例如,它可能能很好地处理机器精度数字,但不能处理任意精度数字)。默认情况下,运行中的编译代码会生成一条信息,并在无法处理某些问题时恢复到普通的 Wolfram 语言评估:
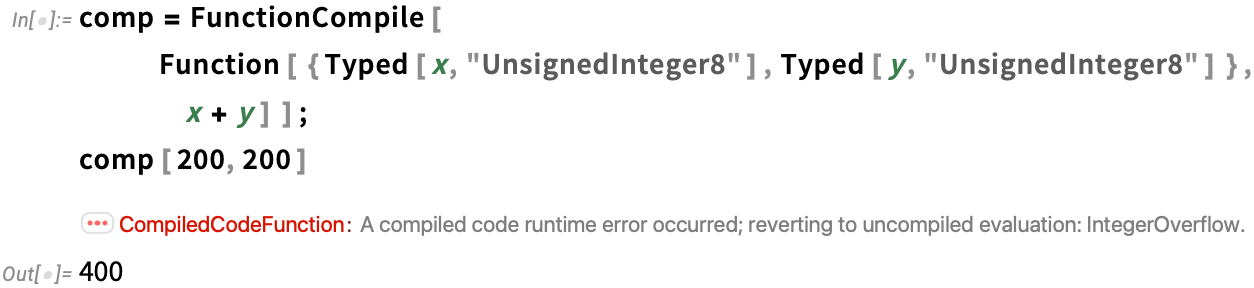
But in Version 14.1 there a new option CompilerRuntimeErrorAction that lets you specify an action to take (or, in general, a function to apply) whenever a runtime error occurs. A setting of None aborts the whole computation if there’s a runtime error:
但在 14.1 版中,有一个新选项 CompilerRuntimeErrorAction 可以让您指定在运行时出错时要采取的行动(或一般情况下要应用的函数)。如果出现运行时错误, None 的设置会中止整个计算:
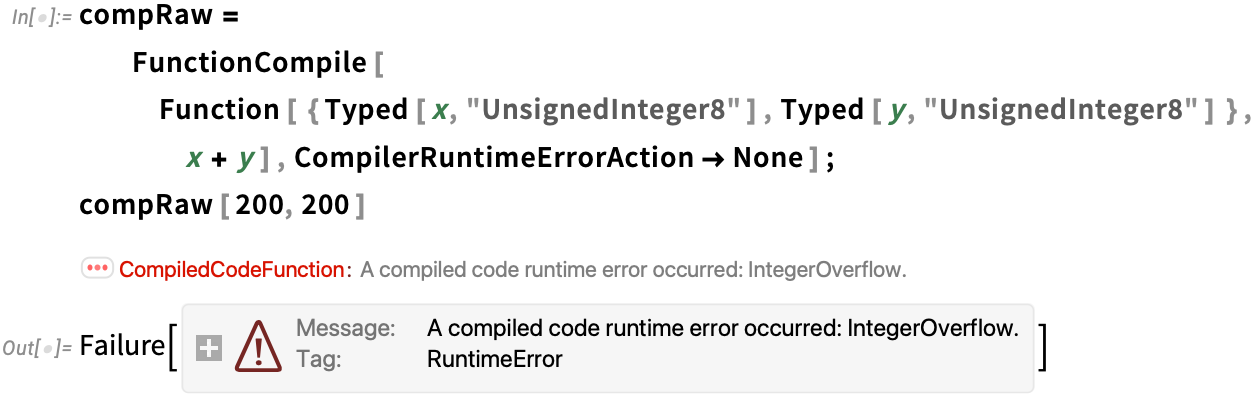
Even Smoother Integration with External Languages
与外部语言更顺畅的集成
Let’s say there’s some functionality you want to use, but the only implementation you have is in a package in some external language, like Python. Well, it’s now basically seamless to work with such functionality directly in the Wolfram Language—plugging into the whole symbolic framework and functionality of the Wolfram Language.
比方说,您想使用某些功能,但唯一的实现方式是在某种外部语言(如 Python)的软件包中。那么,现在基本上可以直接在 Wolfram 语言中无缝地使用这些功能--直接插入 Wolfram 语言的整个符号框架和功能。
As a simple example, here’s a function that uses the Python package faker to produce a random sentence (which of course would also be straightforward to do directly in Wolfram Language):
举个简单的例子,下面是一个使用 Python 软件包 faker 生成随机句子的函数(当然也可以直接在 Wolfram 语言中实现):

The first time you run RandomSentence, the progress monitor will show you all sorts of messy things happening under the hood, as Python versions get loaded, dependencies get set up, and so on. But the point is that it’s all automatic, and so you don’t have to worry about it. And in the end, out pops the answer:
第一次运行 RandomSentence 时,进度监视器会显示在引擎盖下发生的各种乱七八糟的事情,如 Python 版本加载、依赖关系设置等等。但重点是,这些都是自动进行的,所以你不必担心。最后,答案就出来了:

And if you run the function again, all the setup will already have been done, and the answer will pop out immediately:
如果您再次运行该函数,所有设置都已完成,答案会立即弹出:
An important piece of automation here is the conversion of data types. One of the great things about the Wolfram Language is that it has fully integrated symbolic representations for a very wide range of things—from videos to molecules to IP addresses. And when there are standard representations for these things in a language like Python, we’ll automatically convert to and from them.
数据类型的转换是自动化的重要一环。Wolfram 语言的一大优点是,它完全集成了各种事物的符号表示法,从视频到分子,再到 IP 地址。当像 Python 这样的语言中存在这些事物的标准表示法时,我们就会自动进行转换。
But particularly with more sophisticated packages, there’ll be a need to let the package deal with its own “external objects” that are basically opaque to the Wolfram Language, but can be handled as atomic symbolic constructs there.
但是,特别是对于更复杂的软件包,有必要让软件包处理自己的 "外部对象",这些对象对于 Wolfram 语言来说基本上是不透明的,但在 Wolfram 语言中可以作为原子符号构造来处理。
For example, let’s say we’ve started a Python external package chess (and, yes, there’s a paclet in the Wolfram Paclet Repository that has considerably more chess functionality):
例如,假设我们启动了一个 Python 外部软件包 chess (没错,Wolfram Paclet Repository 中有一个 paclet 具有更多的国际象棋功能):

Now the state of a chessboard can be represented by an external object:
现在,棋盘的状态可以用外部对象来表示:

We can define a function to plot the board:
我们可以定义一个函数来绘制电路板:
And now in Version 14.1 you can just pass your external object to the external function:
现在,在 14.1 版中,您只需将外部对象传递给外部函数即可:
You can also directly extract attributes of the external object:
您还可以直接提取外部对象的属性:
And you can call methods (here to make a chess move), changing the state of the external object:
你还可以调用方法(这里是下棋),改变外部对象的状态:

Here’s a plot of a new board configuration:
下面是新电路板的配置图:
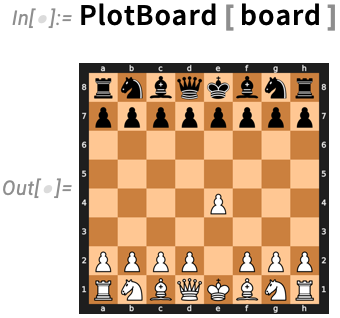
This computes all legal moves from the current position, representing them as external objects:
它会计算从当前位置开始的所有合法移动,并将其表示为外部对象:
Here are UCI string representations of these:
以下是 UCI 字符串表示法:

In what we’re doing here we’re immediately performing each external operation. But Version 14.1 introduces the construct ExternalOperation which lets you symbolically represent an external operation, and for example build up collections of such operations that can all be performed together in a single external evaluation. ExternalObject supports various built-in operations for each environment. So, for example, in Python we can use Call and GetAttribute to get the symbolic representation:
在这里,我们将立即执行每个外部操作。但是,14.1 版引入了 ExternalOperation 结构,它可以让您用符号表示外部操作,例如,可以建立此类操作的集合,在一次外部评估中一并执行。 ExternalObject 支持每个环境的各种内置操作。因此,例如在 Python 中,我们可以使用 Call 和 GetAttribute 获得符号表示:
If we evaluate this, all these operations will get done together in the external environment:
如果我们对此进行评估,所有这些操作都将在外部环境中一并完成:
Standalone Wolfram Language Applications!
独立的 Wolfram 语言应用程序!
Let’s say you’re writing an application in pretty much any programming language—and inside it you want to call Wolfram Language functionality. Well, you could always do that by using a web API served from the Wolfram Cloud. And you could also do it locally by running the Wolfram Engine. But in Version 14.1 there’s something new: a way of integrating a standalone Wolfram Language runtime right into your application. The Wolfram Language runtime is a dynamic library that you link into your program, and then call using a C-based API. How big is the runtime? Well, it depends on what you want to use in the Wolfram Language. Because we now have the technology to prune a runtime to include only capabilities needed for particular Wolfram Language code. And the result is that adding the Wolfram Language will often increase the disk requirements of your application only by a remarkably small amount—like just a few hundred megabytes or even less. And, by the way, you can distribute the Wolfram runtime as an integrated part of an application, with its users not needing their own licenses to run it.
假设您正在使用几乎所有编程语言编写应用程序,并希望在其中调用 Wolfram 语言的功能。您可以使用 Wolfram Cloud 提供的网络 API 来实现这一目的。您也可以在本地运行 Wolfram 引擎。但在 14.1 版中有一些新功能:将独立的 Wolfram 语言运行时直接集成到您的应用程序中。Wolfram 语言运行时是一个动态库,您可以将其链接到程序中,然后使用基于 C 语言的应用程序接口调用。运行时有多大?这取决于您想在 Wolfram 语言中使用什么。因为我们现在拥有的技术可以对运行时进行剪裁,使其只包含特定 Wolfram 语言代码所需的功能。因此,添加 Wolfram 语言通常只会增加应用程序的磁盘需求,而且增加的数量非常少,只有几百兆甚至更少。此外,您还可以将 Wolfram 运行时作为应用程序的一个集成部分进行发布,用户无需获得自己的许可证即可运行 Wolfram 运行时。
OK, so how does creating a standalone Wolfram-enabled application actually work? There’s a lot of software engineering (associated with the Wolfram Language runtime, how it’s called, etc.) under the hood. But at the level of the application programmer you only have to deal with our Standalone Applications SDK—whose interface is rather simple.
那么,创建一个支持 Wolfram 的独立应用程序究竟是如何实现的呢?这需要大量的软件工程(与 Wolfram 语言运行时、如何调用等相关)。但在应用程序编程人员层面,您只需使用我们的独立应用程序 SDK,其界面非常简单。
As an example, here’s the C code part of a standalone application that uses the Wolfram Language to identify what (human) language a piece of text is in. The program here takes a string of text on its command line, then runs the Wolfram Language LanguageIdentify function on it, and then prints a string giving the result:
举例来说,下面是一个独立应用程序的 C 代码部分,它使用 Wolfram 语言来识别一段文本所使用的(人类)语言。该程序在命令行中接收一串文本,然后运行 Wolfram 语言的 LanguageIdentify 函数,最后打印出一个字符串,给出结果:

If we ignore issues of pruning, etc. we can compile this program just with (and, yes, the file paths are necessarily a bit long):
如果不考虑剪枝等问题,我们只需编译这个程序即可(当然,文件路径必然有点长):

Now we can run the resulting executable directly from the command line—and it’ll act just like any other executable, even though inside it’s got all the power of a Wolfram Language runtime:
现在,我们可以直接从命令行运行生成的可执行文件--它的运行方式与其他可执行文件无异,尽管其内部拥有 Wolfram 语言运行时的所有功能:
![]()
If we look at the C program above, it basically begins just by starting the Wolfram Language runtime (using WLR_SDK_START_RUNTIME()). But then it takes the string (argv[1]) from the command line, embeds it in a Wolfram Language expression LanguageIdentify[string], evaluates this expression, and extracts a raw string from the result.
如果我们看一下上面的 C 程序,它基本上只是从启动 Wolfram 语言运行时开始(使用 WLR_SDK_START_RUNTIME() )。但随后它会从命令行中获取字符串 (argv[1]) ,将其嵌入 Wolfram 语言表达式 LanguageIdentify [ string ] ,对该表达式进行求值,并从结果中提取原始字符串。
The functions, etc. that are involved here are part of the new Expression API supported by the Wolfram Language runtime dynamic library. The Expression API provides very clean capabilities for building up and taking apart Wolfram Language expressions from C. There are functions like wlr_Symbol("string") that form symbols, as well as macros like
这里涉及的函数等是 Wolfram 语言运行时动态库支持的新表达式 API 的一部分。Expression API 为从 C 语言构建和拆分 Wolfram 语言表达式提供了非常简洁的功能。有一些函数,如 wlr_ Symbol (" string ") 可以形成符号、以及像
How does the Expression API relate to WSTP? WSTP (“Wolfram Symbolic Transfer Protocol”) is our protocol for transferring symbolic expressions between processes. The Expression API, on the other hand, operates within a single process, providing the “glue” that connects C code to expressions in the Wolfram Language runtime.
Expression API 与 WSTP 有什么关系?WSTP("Wolfram 符号传输协议")是我们用于在进程间传输符号表达式的协议。另一方面,Expression API 在单个进程内运行,提供连接 C 代码与 Wolfram 语言运行时中表达式的 "粘合剂"。
One example of a real-world use of our new Standalone Applications technology is the LSPServer application that will soon be in full distribution. LSPServer started from a pure (though somewhat lengthy) Wolfram Language paclet that provides Language Server Protocol services for annotating Wolfram Language code in programs like Visual Studio Code. To build the LSPServer standalone application we just wrote a tiny C program that calls the paclet, then compiled this and linked it against our Standalone Applications SDK. Along the way (using tools that we’re planning to soon make available)—and based on the fact that only a small part of the full functionality of the Wolfram Language is needed to support LSPServer—we pruned the Wolfram Language runtime, in the end getting a complete LSPServer application that’s only about 170 MB in size, and that shows no outside signs of having Wolfram Language functionality inside.
我们新的独立应用程序技术在现实世界中的一个应用实例是即将全面发布的 LSPServer 应用程序。LSPServer 源自一个纯粹的 Wolfram 语言小程序(虽然有些冗长),它为在 Visual Studio Code 等程序中注释 Wolfram 语言代码提供语言服务器协议服务。为了构建 LSPServer 独立应用程序,我们只需编写一个调用 paclet 的小 C 程序,然后将其编译并与我们的独立应用程序 SDK 相链接。在此过程中(使用我们计划很快推出的工具),基于支持 LSPServer 只需要 Wolfram 语言全部功能中的一小部分这一事实,我们对 Wolfram 语言运行时进行了删减,最终得到了一个完整的 LSPServer 应用程序,其大小仅为 170 MB 左右,而且没有任何外部迹象表明其内部包含 Wolfram 语言功能。
And Yet More… 还有更多...
Is that all? Well, no. There’s more. Like new formatting of Root objects (yes, I was frustrated with the old one). Or like a new drag-and-drop-to-answer option for QuestionObject quizzes. Or like all the documentation we’ve added for new types of entities and interpreters.
就这些?嗯,没有。还有更多。比如 Root 对象的新格式(是的,我对旧格式很不满意)。或者像 QuestionObject 测验的新拖放到答案选项。或者像我们为新型实体和解释器添加的所有文档。
In addition, there’s also the continual stream of new data that we’ve curated, or that’s flowed in real time into the Wolfram Knowledgebase. And beyond the core Wolfram Language itself, there’ve also been lots of functions added to the Wolfram Function Repository, lots of paclets added to the Wolfram Language Paclet Repository, not to mention new entries in the Wolfram Neural Net Repository, Wolfram Data Repository, etc.
此外,我们还不断整理新数据,或将其实时导入Wolfram知识库。除了核心 Wolfram 语言本身,Wolfram 函数库中还添加了大量函数、Wolfram 语言 Paclet 资源库中添加了大量 paclet,更不用说 Wolfram 神经网络资源库、Wolfram 数据资源库中的新条目等等。
Yes, as always it’s been a lot of work. But today it’s here, and we’re proud of it: Version 14.1!
是的,一如既往,我们做了大量的工作。但今天,它来了,我们为此感到自豪:14.1 版!
Posted in: Mathematica, New Technology, Wolfram Language
发布在:Mathematica, New Technology, Wolfram Language





