Abstract 摘要
Single-cell RNA sequencing allows us to model cellular state dynamics and fate decisions using expression similarity or RNA velocity to reconstruct state-change trajectories; however, trajectory inference does not incorporate valuable time point information or utilize additional modalities, whereas methods that address these different data views cannot be combined or do not scale. Here we present CellRank 2, a versatile and scalable framework to study cellular fate using multiview single-cell data of up to millions of cells in a unified fashion. CellRank 2 consistently recovers terminal states and fate probabilities across data modalities in human hematopoiesis and endodermal development. Our framework also allows combining transitions within and across experimental time points, a feature we use to recover genes promoting medullary thymic epithelial cell formation during pharyngeal endoderm development. Moreover, we enable estimating cell-specific transcription and degradation rates from metabolic-labeling data, which we apply to an intestinal organoid system to delineate differentiation trajectories and pinpoint regulatory strategies.
单细胞 RNA 测序技术使我们能够利用表达相似性或 RNA 速率来建模细胞状态动态和命运决策,从而重构状态转变轨迹;然而,轨迹推断方法未能整合宝贵的时间点信息或利用其他模态数据,而针对这些不同数据视图的方法要么无法结合,要么难以扩展。本文提出 CellRank 2——一个通用且可扩展的框架,能以统一方式处理多达数百万细胞的多视图单细胞数据来研究细胞命运。CellRank 2 在人类造血和内胚层发育过程中,能跨数据模态一致地识别终末状态和命运概率。我们的框架还支持整合实验时间点内及跨时间点的状态转换,利用这一特性,我们揭示了促进咽内胚层发育过程中髓质胸腺上皮细胞形成的基因。此外,我们实现了基于代谢标记数据的细胞特异性转录和降解速率估算,并将其应用于肠道类器官系统以描绘分化轨迹并精确定位调控策略。
Similar content being viewed by others
其他用户正在浏览的相似内容
Main 主页
Single-cell assays uncover cellular heterogeneity at unprecedented resolution and scale, allowing complex differentiation trajectories to be reconstructed using computational approaches1,2,3,4,5. While these trajectory inference (TI) methods have uncovered numerous biological insights6, they are typically designed for snapshot single-cell RNA sequencing data and cannot accommodate additional information relevant for understanding cell-state dynamics, including experimental time points, multi-modal measurements, RNA velocity7,8 and metabolic labeling9,10,11,12,13.
单细胞检测以前所未有的分辨率和规模揭示了细胞异质性,使得利用计算方法重建复杂分化轨迹成为可能 1,2,3,4,5 。虽然这些轨迹推断(TI)方法已揭示众多生物学见解 6 ,但它们通常针对单细胞 RNA 测序快照数据设计,无法兼容理解细胞状态动力学所需的其他信息,包括实验时间点、多模态测量、RNA 速率 7,8 和代谢标记 9,10,11,12,13 。
We, and others, have developed methods to analyze emerging data modalities, such as CellRank14 for RNA velocity, Waddington optimal transport (WOT)15 for experimental time points and dynamo16 for metabolic-labeling data; however, each method only addresses a single modality, thereby ignoring much of the upcoming multi-modal information for trajectory analysis. This specialization renders many biological systems inaccessible; for example, adult hematopoiesis violates assumptions of current RNA velocity models17, precluding us from applying CellRank to this well-studied system and prompting the question of whether the algorithm could be developed further to reconstruct differentiation dynamics using another aspect of these data.
我们及其他研究者已开发出多种方法来分析新兴数据模态,例如用于 RNA 速率的 CellRank 14 、针对实验时间点的 Waddington 最优输运(WOT) 15 以及处理代谢标记数据的 dynamo 16 ;然而每种方法仅针对单一模态,因而忽略了轨迹分析中即将涌现的多模态信息。这种专门化导致许多生物系统无法被研究:例如,成年造血过程违背了现有 RNA 速率模型的假设 17 ,使我们无法将 CellRank 应用于这一被深入研究的系统,进而引发思考——能否通过进一步开发算法,利用这些数据的其他方面来重建分化动态。
To address this challenge, we decompose TI into two components, modality-specific modeling of cell transitions, followed by modality-agnostic TI, and developed CellRank 2, a robust, modular framework to analyze multiview data from millions of cells. CellRank 2 generalizes CellRank to exploit the full potential of alternative sources of information, such as pseudotime and developmental potential, and new data modalities, such as experimental time points and metabolic labels, to study complex cellular state changes and identify initial and terminal states, fate probabilities and lineage-correlated genes. Compared to our earlier work, the new framework is modular, applicable to many more data modalities and substantially faster (Methods).
为应对这一挑战,我们将轨迹推断分解为两个组成部分:细胞转变的模态特异性建模和模态无关的轨迹推断,并开发了 CellRank 2——一个强大、模块化的框架,用于分析数百万细胞的多视图数据。CellRank 2 将 CellRank 推广至充分利用替代信息源(如伪时间和发育潜能)及新型数据模态(如实验时间点和代谢标记)的全部潜力,以研究复杂的细胞状态变化,识别初始与终末状态、命运概率及谱系相关基因。相较于先前工作,新框架采用模块化设计,可适配更多数据模态且计算效率显著提升(详见方法部分)。
We demonstrate CellRank 2’s flexibility across a series of applications: using a pseudotime in a hematopoiesis context, determining developmental potentials during embryoid body formation and combining experimental time points with intra-time point information for pharyngeal endoderm development. Our approach for incorporating experimental time recovers terminal states more faithfully compared to traditional approaches mapping between time points15, allows studying gene expression change continuously across time and predicts putative progenitors missed by alternative approaches. We also introduce a new computational approach for learning cellular dynamics from metabolic-labeling data and show that it reveals regulatory mechanisms by recovering cell-specific transcription and degradation rates in mouse intestinal organoids.
我们通过一系列应用展示了 CellRank 2 的灵活性:在造血过程中使用伪时间、确定胚状体形成期间的发育潜能,以及将实验时间点与咽内胚层发育的时点内信息相结合。相较于传统的时间点间映射方法 15 ,我们整合实验时间的方法能更真实地还原终末状态,允许连续研究跨时间的基因表达变化,并预测其他方法遗漏的假定祖细胞。我们还提出了一种新的计算方法,用于从代谢标记数据中学习细胞动力学,并通过恢复小鼠肠道类器官中细胞特异性转录和降解速率来揭示调控机制。
Results 结果
A modular framework for studying state-change trajectories
研究状态转变轨迹的模块化框架
CellRank 2 models cell-state dynamics from multiview single-cell data. It automatically determines initial and terminal states, computes fate probabilities, charts trajectory-specific gene expression trends and identifies lineage-correlated genes (Methods). A broad and extensible range of biological scenarios can be studied using its robust, scalable and modular design (Methods).
CellRank 2 通过多视角单细胞数据建模细胞状态动态。它能自动识别初始与终末状态,计算命运概率,绘制轨迹特异性基因表达趋势,并鉴定谱系相关基因(方法部分)。其稳健、可扩展且模块化的设计支持研究广泛而多样的生物学场景(方法部分)。
Similar to CellRank14, we employ a probabilistic system description wherein each cell constitutes one state in a Markov chain with edges representing cell–cell transition probabilities; however, we now enable deriving these transition probabilities from various biological priors. Following previous successful TI approaches1,2,3,4,5, we assume gradual, memoryless transitions of cells along the phenotypic manifold. The assumption of memoryless transitions is justified as we model average cellular behavior (Methods).
与 CellRank 14 类似,我们采用概率化系统描述——每个细胞构成马尔可夫链中的一个状态,边代表细胞间转移概率;但我们现在支持从多种生物学先验中推导这些转移概率。沿袭先前成功的轨迹推断方法 1,2,3,4,5 ,我们假设细胞沿表型流形发生渐进、无记忆的迁移。这种无记忆迁移假设是合理的,因为我们建模的是细胞的平均行为(方法部分)。
To allow broad applicability, we divide CellRank 2 into kernels for computing a cell–cell transition matrix based on multiview single-cell data and estimators for analyzing the transition matrix to identify initial and terminal states, compute fate probabilities and perform other downstream tasks. CellRank 2 provides a set of diverse kernels that derive transition probabilities based on gene expression, RNA velocity, pseudotime, developmental potentials, experimental time points and metabolically labeled data (Fig. 1a and Extended Data Fig. 1). Depending on the dataset and the biological question, we use a single kernel or combine several kernels into multiview Markov chains. For an initial, qualitative overview of recovered cellular dynamics, we introduce a random walk-based visualization scheme (Methods).
为了实现广泛适用性,我们将 CellRank 2 划分为两个核心模块:基于多视角单细胞数据计算细胞间转移矩阵的核函数(kernels),以及通过分析转移矩阵来识别初始/终末状态、计算命运概率并执行其他下游任务的估计器(estimators)。CellRank 2 提供了一套多样化核函数,可基于基因表达、RNA 速率、伪时序、发育潜能、实验时间点和代谢标记数据推导转移概率(图 1a 和扩展数据图 1)。根据数据集和生物学问题的特点,我们可单独使用某个核函数,或将多个核函数组合成多视角马尔可夫链。为了对重建的细胞动力学进行初步定性分析,我们还引入了基于随机游走的可视化方案(方法部分)。
图 1:CellRank 2 提供了一个基于马尔可夫链的统一框架来研究单细胞命运决策。
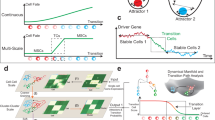
CellRank 2 uses a modular design. Data and problem-specific kernels calculate a cell–cell transition matrix inducing a Markov chain (MC); of these kernels, at least one has to be used, but multiple can be combined via a kernel combination (Methods). Estimators analyze the MC to infer initial and terminal states, fate probabilities and lineage-correlated genes. Using fate probabilities and a pseudotime allows for studying gene expression changes during lineage priming. Features inherited from the original CellRank implementation are indicated in blue and new features are in orange.
CellRank 2 采用模块化设计。数据和特定问题内核通过计算细胞间转移矩阵来构建马尔可夫链(MC);这些内核中至少需使用一个,但可通过内核组合方法进行多内核整合(Methods)。估计器通过分析 MC 来推断初始与终末状态、命运概率及谱系相关基因。结合命运概率与伪时间可研究谱系启动过程中的基因表达变化。继承自原始 CellRank 的功能以蓝色标注,新增功能以橙色标识。
For many biological processes, the starting point can be quantified robustly and cells ordered along a pseudotime. We propose to use this fact by biasing the edges of a nearest-neighbor graph toward mature cell states to estimate cell–cell transitions (Methods); developmental potentials can be used similarly. CellRank 2 generalizes earlier concepts5,18 to arbitrary pseudotimes and atlas-scale datasets with the PseudotimeKernel and CytoTRACEKernel. More complex systems with unknown initial states or longer developmental time scales can be captured faithfully through multiple experimental time points. To reconstruct the overall differentiation dynamics described by both across and within time points, we extend classical optimal transport (OT)15, in particular WOT15, with our RealTimeKernel to include within-time-point dynamics (Methods). In contrast, metabolic labels offer an experimental approach to overcome the discrete nature of distinct experimental time points9,11,12. Based on this information, we developed an inference approach quantifying kinetic rates that allow us to infer cell transitions (Methods). In the following, we provide details on each kernel and demonstrate the versatility of our approach through diverse applications. Finally, various kernels may be combined to yield a more complete picture of cellular dynamics through multiview modeling.
在许多生物过程中,起始点能够被稳健量化,细胞可沿伪时间轴排序。我们提出利用这一特性,通过将最近邻图的边权重偏向成熟细胞状态来估算细胞间转换(方法部分);发育潜能可同理运用。CellRank 2 通过伪时间核(PseudotimeKernel)和细胞轨迹评估核(CytoTRACEKernel)将早期概念 5,18 推广至任意伪时间尺度和图谱级数据集。对于初始状态未知或发育时间跨度更长的复杂系统,可通过多个实验时间点实现精准捕捉。为重构跨时间点与时间点内共同描述的整体分化动态,我们基于经典最优传输理论(OT) 15 (特别是 WOT 15 )扩展出实时核(RealTimeKernel),以纳入时间点内动态(方法部分)。相比之下,代谢标记技术提供了克服离散实验时间点局限的实验方案 9,11,12 。基于此信息,我们开发了量化动力学速率的推断方法,从而推演细胞状态转换(方法部分)。 下文我们将详细介绍每种核函数,并通过多样化的应用展示我们方法的通用性。最后,通过多视图建模整合不同核函数,可以更全面地展现细胞动态变化。
Once we have inferred a transition matrix, we use an estimator module19,20 to uncover cellular trajectories, including initial and terminal states, fate probabilities and lineage-correlated genes. Critically, estimators are view-independent and are, thus, applicable to any transition matrix (Methods). To scale these computations to large datasets, we assume that each cell gives rise to only a small set of potential descendants. This assumption yields sparse transition matrices for every kernel and allows CellRank 2 to compute fate probabilities 30 times faster than CellRank (Extended Data Fig. 2a and Methods).
一旦推断出转移矩阵,我们便使用估计器模块 19,20 来揭示细胞轨迹,包括初始与终末状态、命运概率及谱系相关基因。关键在于,这些估计器具有视图无关性,因此可适用于任何转移矩阵(详见方法部分)。为将此类计算扩展至大规模数据集,我们假设每个细胞仅能产生少量潜在后代。这一假设使得每个核函数生成的转移矩阵保持稀疏性,从而使 CellRank 2 计算命运概率的速度比 CellRank 快 30 倍(扩展数据图 2a 及方法部分)。
The modular and robust design makes CellRank 2 a flexible framework for the probabilistic analysis of state dynamics in multiview single-cell data; it enables the rapid adaptation of computational workflows to emerging data modalities, including lineage tracing21,22,23 and spatiotemporal data24, the support of new data modalities with kernels and the support of new analyses with estimators (Methods).
模块化且稳健的设计使 CellRank 2 成为多视角单细胞数据状态动态概率分析的灵活框架;它能快速适应新兴数据模态(包括谱系追踪 21,22,23 和时空数据 24 )的计算流程,通过内核支持新数据模态,并通过估计器支持新分析方法(详见方法部分)。
Overcoming RNA velocity limitations
克服 RNA 速度的局限性
RNA velocity infers incorrect dynamics in steady-state human hematopoiesis due to violated model assumptions, even though pseudotime can be recovered faithfully (Supplementary Fig. 1 and Supplementary Note 1). Specifically, the assumption of constant rates made by conventional RNA velocity models is violated and genes important for this system exhibit high noise or low coverage. The remarkable success of traditional pseudotime approaches in systems with well-known initial conditions motivated us to circumvent RNA velocity limitations by developing the PseudotimeKernel, which computes pseudotime-informed transition probabilities and a corresponding vector field (Fig. 2a and Methods). Building upon conceptual ideas proposed for Palantir5, our approach generalizes to any precomputed pseudotime and uses a soft weighting scheme25.
RNA 速率在稳态人类造血过程中因违反模型假设而推断出错误的动力学(尽管伪时间能够被准确重建,见补充图 1 和补充说明 1)。具体而言,传统 RNA 速率模型所假设的恒定速率条件被打破,且对该系统重要的基因表现出高噪声或低覆盖率。传统伪时间方法在初始条件明确的系统中取得的显著成功,促使我们通过开发 PseudotimeKernel 来规避 RNA 速率的局限性——该内核可计算伪时间信息化的转移概率及相应向量场(图 2a 和方法部分)。基于 Palantir 5 提出的概念框架,我们的方法可推广至任何预计算的伪时间,并采用软加权方案 25 。
图 2:利用伪时序排序进行细胞命运图谱构建。
a, The PseudotimeKernel biases the edges of a phenotypic similarity-based nearest-neighbor graph toward increasing pseudotime, defining cell–cell transition probabilities. b,c, UMAP embedding of 24,440 peripheral blood mononuclear cells26, colored by cell type (cDC; G/M progenitor, granulocyte/myeloid progenitor; HSC; MK/E prog, megakaryocyte/erythrocyte progenitors; pDC). We illustrate the well-known differentiation hierarchy in black (b) as well as projected velocity fields based on the PseudotimeKernel (c, left) and RNA velocity (c, right). d, Correlating fate probabilities with gene expression recovers known lineage drivers for the pDC lineage27,28. We show lineage-specific trends as proposed in our earlier work14 by fitting generalized additive models to gene expression (y axis) in pseudotime (x axis); the contribution of each cell to each lineage is weighted according to CellRank 2-recovered fate probabilities. Colors correspond to lineages as shown in b.
a, PseudotimeKernel 通过使基于表型相似性的最近邻图的边偏向伪时间增加方向,定义细胞间转移概率。b,c, 24,440 个外周血单个核细胞 26 的 UMAP 嵌入图,按细胞类型着色(cDC;G/M 祖细胞,粒细胞/髓系祖细胞;HSC;MK/E 祖细胞,巨核细胞/红细胞祖细胞;pDC)。黑色线条标示已知分化层级(b),基于 PseudotimeKernel(c 左)和 RNA 速率(c 右)的投射速度场。d, 将命运概率与基因表达关联可识别 pDC 谱系已知驱动基因 27,28 。通过广义加性模型拟合基因表达(y 轴)与伪时间(x 轴)关系,按 CellRank 2 推算的命运概率加权各细胞对谱系贡献,展示我们早期工作 14 提出的谱系特异性趋势。颜色对应 b 图所示谱系。
We applied the PseudotimeKernel to human hematopoiesis26 and computed transition probabilities based on diffusion pseudotime (DPT)1 for the normoblast, monocyte and dendritic cell lineages (Fig. 2b and Extended Data Fig. 3a). The PseudotimeKernel correctly recovered all four terminal states and the initial state (Extended Data Fig. 3b,c and Methods). To additionally visualize the recovered dynamics, we generalized the streamline projection scheme from RNA velocity7,8 to any neighbor-graph-based kernel (Fig. 2c and Methods). We correlated gene expression with lineage-specific fate probabilities to identify candidate genes that may be involved in lineage commitment (Methods); this approach correctly identified the transcription factors RUNX2 and TCF4 as regulators of the plasmacytoid dendritic cell (pDC) lineage27,28 (Fig. 2d).
我们将 PseudotimeKernel 应用于人类造血系统 26 ,并基于扩散伪时间(DPT) 1 计算了正成红细胞、单核细胞和树突状细胞谱系的转移概率(图 2b 和扩展数据图 3a)。该算法正确还原了所有四个终末状态及初始状态(扩展数据图 3b,c 及方法部分)。为进一步可视化恢复的动态过程,我们将 RNA 速率 7,8 的流线投影方案推广至任意基于邻域图的核函数(图 2c 及方法)。通过关联基因表达与谱系特异性命运概率,我们筛选出可能参与谱系定向的候选基因(方法部分);该方法准确识别了转录因子 RUNX2 和 TCF4 作为浆细胞样树突状细胞(pDC)谱系 27,28 的调控因子(图 2d)。
Compared to the PseudotimeKernel, an RNA velocity-based analysis failed to recover the classical dendritic cell (cDC) lineage (Extended Data Fig. 3b) and fate probabilities assigned by the VelocityKernel violated the known lineage commitment and hierarchy, including high transition probabilities from proerythroblast and erythroblast cells to monocytes instead of normoblasts (Extended Data Fig. 3d). This inconsistency to known ground truth transitions stems from violated assumptions of the RNA velocity model (Supplementary Fig. 1 and Supplementary Note 1). For an additional, quantitative metric, we computed the log ratio of the kernels’ cross-boundary correctness (CBC) scores29 (Methods). This metric provides a quantitative measure of two kernel-derived cell–cell transition matrices for known transitions between cell states. As indicated by the visualization of fate probabilities, the PseudotimeKernel significantly outperforms the competing approach for most cell state transitions (6 out of 8; Extended Data Fig. 3e and Methods). As an alternative comparison, we introduce the terminal state identification (TSI) score to quantify the identification of known terminal states compared to an optimal identification strategy (TSI = 1; Methods). Our pseudotime-based approach again outperformed the RNA-velocity-based alternative (TSI = 0.9 versus TSI = 0.81; Extended Data Fig. 3f).
与 PseudotimeKernel 相比,基于 RNA 速度的分析未能恢复经典树突状细胞(cDC)谱系(扩展数据图 3b),且 VelocityKernel 分配的命运概率违背了已知的谱系定向与层级关系,例如前成红细胞和成红细胞向单核细胞而非正成红细胞的高转移概率(扩展数据图 3d)。这种与已知真实转移过程的不一致性源于 RNA 速度模型的假设被违反(附图 1 和补充说明 1)。作为额外的量化指标,我们计算了内核跨边界正确性(CBC)分数对数值 29 (方法部分)。该指标通过量化两种内核衍生的细胞间转移矩阵,评估已知细胞状态间转移的准确性。如命运概率可视化所示,PseudotimeKernel 在大多数细胞状态转移中显著优于对比方法(8 例中有 6 例;扩展数据图 3e 及方法部分)。 作为替代性比较,我们引入了终态识别(TSI)评分来量化已知终态识别与最优识别策略的对比(TSI = 1;方法部分)。基于伪时间的方案再次优于基于 RNA 速率的替代方案(TSI = 0.9 对比 TSI = 0.81;扩展数据图 3f)。
Our PseudotimeKernel generalizes to any pseudotime, allowing users to choose the algorithm most suitable for their dataset30. In systems with simpler differentiation hierarchies and known initial states, CellRank 2’s PseudotimeKernel yields additional insights into terminal states and fate commitment compared to classical pseudotime approaches.
我们的 PseudotimeKernel 可推广至任意伪时序,允许用户选择最适合其数据集的算法 30 。在具有较简单分化层级和已知初始状态的系统中,与经典伪时序方法相比,CellRank 2 的 PseudotimeKernel 能提供关于终末状态和命运决定的更深层次见解。
Learning vector fields from developmental potentials
从发育潜能中学习向量场
Pseudotime inference requires the initial state to be specified. If the initial state is not known, CytoTRACE18 can be used to infer a stemness score by assuming that, on average, naive cells express more genes than mature cells. We found this assumption to be effective for many early developmental scenarios, but, critically, CytoTRACE does not scale in time and memory usage when applied to large datasets and does not resolve individual trajectories through terminal states and fate probabilities (Extended Data Fig. 2b). We thus developed the CytoTRACEKernel by revising the original CytoTRACE approach, such that edges of k-nearest-neighbor graphs point toward increasing maturity and quantify cell–cell transition probabilities on atlas-scale datasets (Extended Data Fig. 4a and Methods). Results from our kernel agree with the original approach across multiple datasets (Extended Data Fig. 4b,c and Methods). Further, we compared computational performance on a mouse organogenesis atlas31 containing 1.3 million cells. While the original implementation failed above 80,000 cells, our adaptation ran on the full dataset in under 2 min (Extended Data Fig. 2b).
伪时间推断需要指定初始状态。若初始状态未知,可使用 CytoTRACE 18 通过假设幼稚细胞平均比成熟细胞表达更多基因来推断干性评分。我们发现这一假设对许多早期发育场景有效,但关键在于,CytoTRACE 在处理大规模数据集时无法实现时间和内存使用效率的扩展,且无法解析通过终末状态和命运概率的个体轨迹(扩展数据图 2b)。因此,我们通过改进原始 CytoTRACE 方法开发了 CytoTRACEKernel,使 k 近邻图的边指向成熟度递增方向,并在图谱级数据集上量化细胞间转移概率(扩展数据图 4a 和方法)。我们的内核结果与原始方法在多个数据集上保持一致(扩展数据图 4b、c 和方法)。此外,我们在包含 130 万个细胞的小鼠器官发生图谱 31 上比较了计算性能:原始实现在超过 8 万个细胞时失效,而我们的改进版本可在 2 分钟内完成全数据集分析(扩展数据图 2b)。
We applied the CytoTRACEKernel to study endoderm development in pluripotent cell aggregates known as embryoid bodies32 (Fig. 3a). The CytoTRACE-based pseudotime increased smoothly throughout all experimental time points, as expected (Fig. 3b and Extended Data Fig. 5a) and allowed us to identify 10 of 11 terminal cell populations and the correct initial state (Fig. 3c and Extended Data Fig. 5b). In contrast, Palantir5 and DPT1 identified a bimodal population distribution of early cells in the first stage, resulting in a compressed range of pseudotimes for all other populations and stages (Extended Data Fig. 5a).
我们应用 CytoTRACEKernel 研究了多能细胞聚集体(即类胚体 32 )中的内胚层发育(图 3a)。基于 CytoTRACE 的伪时间在所有实验时间点均呈现预期中的平滑增长(图 3b 和扩展数据图 5a),并成功识别出 11 个终末细胞群体中的 10 个及正确的初始状态(图 3c 和扩展数据图 5b)。相比之下,Palantir 5 和 DPT 1 在第一阶段识别出早期细胞的双峰群体分布,导致其他所有群体和阶段的伪时间范围被压缩(扩展数据图 5a)。
图 3:CytoTRACEKernel 重建时序基因激活过程。
a,b, UMAP embedding of 31,029 embryoid body cells32, colored by original cluster annotation (CPs, cardiac precursors; EN, endoderm; EPs, epicardial precursors; ESC, embryonic stem cell; Hem., hemangioblast; ME, mesoderm; NC, neural crest; NE, neuroectoderm; NS, neuronal subtypes; Post. EN, posterior endoderm; SMPs, smooth muscle precursors; a, left), embryo stage (E) (a, right) and pseudotimes from the CytoTRACEKernel (b). c, Terminal states inferred using the CytoTRACEKernel. d, UMAP embedding colored by fate probabilities (top) and gene expression of recovered drivers (bottom) of the endoderm lineage. e, Smoothed gene expression along the CytoTRACE pseudotime for the automatically identified top 50 lineage-correlated genes, sorted according to their pseudotime peak. Genes identified in the original publication (left) and known drivers (right)32,33,34 additionally recovered with CellRank 2 are indicated.
a、b 图展示了 31,029 个胚状体细胞的 UMAP 嵌入结果( 32 ),分别按原始聚类注释(CPs,心脏前体细胞;EN,内胚层;EPs,心外膜前体细胞;ESC,胚胎干细胞;Hem.,成血管细胞;ME,中胚层;NC,神经嵴;NE,神经外胚层;NS,神经元亚型;Post. EN,后内胚层;SMPs,平滑肌前体细胞;a 图左)、胚胎发育阶段(E)(a 图右)以及 CytoTRACEKernel 计算的伪时间(b 图)进行颜色编码。c 图呈现了基于 CytoTRACEKernel 推断的终末状态。d 图的 UMAP 嵌入通过内胚层谱系的命运概率(上)和已识别驱动基因的表达量(下)着色。e 图显示了沿 CytoTRACE 伪时间轴自动筛选的前 50 个谱系相关基因的平滑表达曲线,按伪时间峰值排序。特别标注了原始文献中已发现的基因(左)以及通过 CellRank 2 新识别的已知驱动基因(右)( 32,33,34 )。
The endoderm gives rise to internal organs; thus, we correlated fate probabilities with gene expression to infer lineage-correlated genes that may direct organogenesis, identifying the MIXL1, FOXA2 and SOX17 transcription factors (TFs), in agreement with the original publication32 (Fig. 3d). To uncover potential upstream regulators of these TFs, we visualize smooth gene expression trends of top-ranked lineage-correlated genes of the endoderm trajectory in a heatmap and sorted genes according to their peak in CytoTRACE pseudotime (Fig. 3e). We found LINC00458, LINC01356, NODAL and nine TFs to peak before FOXA2 and SOX17. All are known mouse endodermal development genes33,34 and our prediction that LINC00458 expression peaks before LINC01356 has also been observed previously33.
内胚层发育形成内脏器官;因此,我们将命运概率与基因表达相关联,以推断可能指导器官发生的谱系相关基因,鉴定出 MIXL1、FOXA2 和 SOX17 转录因子(TFs),这与原始出版物 32 的结论一致(图 3d)。为了揭示这些 TFs 的潜在上游调控因子,我们在热图中可视化内胚层轨迹中排名靠前的谱系相关基因的平滑表达趋势,并根据它们在 CytoTRACE 伪时间中的峰值对基因进行排序(图 3e)。我们发现 LINC00458、LINC01356、NODAL 和九个 TFs 的表达峰值出现在 FOXA2 和 SOX17 之前。这些都是已知的小鼠内胚层发育基因 33,34 ,而我们预测 LINC00458 的表达峰值早于 LINC01356 的现象先前也有报道 33 。
CellRank 2’s CytoTRACEKernel allowed us to infer cellular dynamics from a snapshot of endoderm development without having to specify an initial state for pseudotime computation. We recovered terminal states, known driver genes and their temporal activation pattern.
CellRank 2 的 CytoTRACEKernel 使我们能够从内胚层发育的快照中推断细胞动态,而无需为伪时间计算指定初始状态。我们恢复了终末状态、已知驱动基因及其时间激活模式。
Adding a temporal resolution to fate mapping
为命运映射添加时间分辨率
Single-cell time series are increasingly popular for studying non-steady-state differentiation programs. The computational challenge lies in matching cells sequenced at different time points to reconstruct trajectories of state change. Most previous methods have either determined population dynamics35 or used OT15 but ignore transitions within time points that contain valuable information for directing transitions and detecting terminal states. We developed the RealTimeKernel, which combines WOT-computed15 inter-time-point transitions with similarity-based intra-time-point transitions to allow for multiview modeling (Fig. 4a and Methods). Notably, considering inter-time-point transitions enables unbiased identification of terminal and initial states from time-course studies through a more granular mapping of cell fate (Fig. 4b and Extended Data Fig. 6a–c). To gain a preliminary understanding of the underlying differentiation dynamics, we visualize high-dimensional RealTimeKernel-derived random walks in the embedding space (Extended Data Fig. 6b).
单细胞时间序列数据在研究非稳态分化过程中日益受到重视。其计算挑战在于如何匹配不同时间点测序的细胞以重建状态转变轨迹。以往多数方法要么仅确定群体动态 35 ,要么采用最优传输理论 15 ,却忽略了时间点内部蕴含的宝贵过渡信息——这些信息对指导状态转变和检测终末状态至关重要。我们开发的 RealTimeKernel 通过结合 WOT 计算的跨时间点转移 15 与基于相似性的时间点内转移,实现了多视角建模(图 4a 与方法部分)。值得注意的是,考虑跨时间点转移能够通过更精细的细胞命运映射,从时间序列研究中无偏地识别终末状态和初始状态(图 4b 及扩展数据图 6a-c)。为初步理解潜在分化动力学,我们将 RealTimeKernel 推导的高维随机游走可视化于嵌入空间(扩展数据图 6b)。
图 4:通过时间分辨测量推断状态轨迹。
a, The RealTimeKernel combines across time-point transitions from WOT15 with within-time-point transitions from gene expression similarity to account for the asynchrony observed in many cellular processes. All views are combined in a single transition matrix. b, By including within-time-point information, the RealTimeKernel enables recovering more granular state transitions; WOT only considers transitions between consecutive time points. c, UMAP embedding of pharyngeal organ development37 (n = 55,044 cells) colored by embryonic day (E; left) and original cell type annotation (right; cTEC, mTEC, UBB); gray color encodes early, uncommitted cells. d, Using the RealTimeKernel, CellRank 2 correctly identifies 10 out of 11 terminal states. The black outline highlights mTECs and potential precursor cells. e,f, Fate probabilities toward the mTEC terminal state (left) and top 20 lineage-correlated genes identified (right) based on the RealTimeKernel (e) or WOT’s pullback distribution (f). We highlight TFs in yellow and known mTEC development genes in green. CellRank 2 identifies putative drivers by correlating fate probabilities with gene expression, WOT by comparing high- and low-probability cells.
a. RealTimeKernel 通过整合 WOT 15 的时间点间转移与基因表达相似性的时间点内转移,解决了许多细胞过程中观察到的异步性问题。所有视图被整合为单一转移矩阵。
b. 通过纳入时间点内信息,RealTimeKernel 能识别更精细的状态转移;而 WOT 仅考虑连续时间点间的转移。
c. 咽器官发育 37 的 UMAP 嵌入(n=55,044 个细胞)按胚胎天数(E;左图)和原始细胞类型注释着色(右图;cTEC、mTEC、UBB);灰色表示早期未定型细胞。
d. CellRank 2 使用 RealTimeKernel 正确识别了 11 个终末状态中的 10 个。黑色轮廓标出了 mTEC 及其潜在前体细胞。
e,f. 基于 RealTimeKernel(e)或 WOT 的 pullback 分布(f)计算的 mTEC 终末状态命运概率(左图)及前 20 个谱系相关基因(右图)。黄色标注转录因子,绿色标注已知的 mTEC 发育相关基因。 CellRank 2 通过将命运概率与基因表达相关联来识别推定驱动因子,而 WOT 则通过比较高概率和低概率细胞来实现。
Many OT implementations, including WOT15, use entropic regularization36 to speed up computation; however, this practice introduces dense transition matrices, which slows downstream applications, hindering us from analyzing large datasets. We therefore developed an adaptive thresholding scheme to sparsify transition matrices (Methods), yielding ninefold and 56-fold faster macrostate and fate probability computation, respectively, on a mouse embryonic fibroblast (MEF) reprogramming dataset15 (Extended Data Fig. 2c). To validate our thresholding scheme, we correlated fate probabilities toward the four terminal states, with and without thresholding, and found very high correlations within each lineage (Pearson correlation coefficient r > 99; Extended Data Fig. 6c and Methods). Overall, we obtained a perfect TSI score using the RealTimeKernel (TSI = 1) but a suboptimal one for the VelocityKernel (TSI = 0.79) (Extended Data Fig. 6d).
许多 OT 实现(包括 WOT 15 )采用熵正则化 36 来加速计算;然而,这种做法会引入密集的转移矩阵,从而拖慢下游应用,阻碍我们分析大型数据集。为此,我们开发了一种自适应阈值方案来稀疏化转移矩阵(方法部分),在小鼠胚胎成纤维细胞(MEF)重编程数据集 15 上分别实现了宏观状态和命运概率计算的 9 倍与 56 倍加速(扩展数据图 2c)。为验证阈值方案的有效性,我们对比了阈值处理前后四个终末状态的命运概率相关性,发现各谱系内部均保持极高相关性(皮尔逊相关系数 r > 0.99;扩展数据图 6c 及方法部分)。总体而言,使用 RealTimeKernel 时我们获得了完美的 TSI 评分(TSI=1),但 VelocityKernel 的评分次优(TSI=0.79)(扩展数据图 6d)。
Numerous applications, including gene trend plotting and lineage-correlated gene identification, require continuous temporal information rather than discrete time points. Thus, we comprised a new, real-time informed pseudotime approach, which uses experimental time points but embeds them in the continuous landscape of expression changes (Methods). As expected in this system, our new pseudotime indeed correlates better with experimental time than traditional pseudotime approaches on the MEF reprogramming data (Extended Data Fig. 7a–c). Compared to WOT, we enable studying gradual fate establishment along a continuous axis (Extended Data Fig. 7d–g).
包括基因趋势绘图和谱系相关基因鉴定在内的众多应用需要连续的时间信息而非离散时间点。为此,我们构建了一种新型实时信息伪时间方法,该方法利用实验时间点但将其嵌入表达变化的连续景观中(方法部分)。正如在该系统中预期的那样,在 MEF 重编程数据上,我们的新伪时间确实比传统伪时间方法更与实验时间相关(扩展数据图 7a–c)。与 WOT 相比,我们能够沿连续轴研究渐进的命运建立过程(扩展数据图 7d–g)。
The pharyngeal endoderm, an embryonic tissue, plays a crucial role in patterning the pharyngeal region and developing organs37, such as the parathyroid, thyroid and thymus38,39,40. Multiple experimental time points can capture its development, making it an ideal candidate system for our RealTimeKernel. We analyzed gene expression change from embryonic days (E) 9.5 to 12.5 (ref. 37) (Fig. 4c) and automatically recovered the initial state (Extended Data Fig. 8a) and 10 of the 11 terminal states manually assigned in the original publication (Fig. 4d). Additionally, using the RealTimeKernel led to a higher TSI score compared to the VelocityKernel (TSI = 0.92 versus TSI = 0.46, Extended Data Fig. 8b). Correlating fate probabilities with gene expression correctly recovered known lineage drivers of the parathyroid (Gcm2)41, thyroid (Hhex)42 and thymus (Foxn1)37 (Supplementary Fig. 2).
咽内胚层作为一种胚胎组织,在咽区模式形成及器官发育(如甲状旁腺、甲状腺和胸腺)中起关键作用。通过多个实验时间点可捕捉其发育过程,使其成为我们 RealTimeKernel 的理想候选系统。我们分析了胚胎第 9.5 天至 12.5 天(参考文献 37 )的基因表达变化(图 4c),自动重建了初始状态(扩展数据图 8a)及原文献中人工标注的 11 个终末状态中的 10 个(图 4d)。此外,与 VelocityKernel 相比,使用 RealTimeKernel 获得了更高的 TSI 评分(TSI=0.92 对 TSI=0.46,扩展数据图 8b)。通过将命运概率与基因表达相关联,正确识别出已知的甲状旁腺(Gcm2)、甲状腺(Hhex)和胸腺(Foxn1)谱系驱动因子(补充图 2)。
To disentangle the trajectory leading to medullary thymic epithelial cells, a stromal cell type associated with thymic adhesion43, we first took the subset of parathyroid, ultimobranchial body, medullary and cortical thymic epithelial cells (mTECs and cTECs) and their progenitors (Extended Data Fig. 8c and Methods). We successfully recovered the initial state (Extended Data Fig. 8c) and each terminal state and scored a higher TSI metric compared to relying on RNA velocity estimates (TSI = 1.0 versus TSI = 0.91; Extended Data Fig. 8d). Computing fate probabilities toward terminal states, we discovered a progenitor cell cluster with an increased probability of assuming mTEC fate (Fig. 4e and Extended Data Fig. 9a,b). It is easy to overlook this putative mTEC ancestor cluster in the two-dimensional uniform manifold approximation and projection (UMAP) embedding, highlighting the importance of our high-dimensional fate analysis (Extended Data Fig. 9c). Next, we used our correlation-based analysis to identify possible drivers of this fate decision and found TFs (Fos, Grhl3 and Elf5) and genes relevant for the thymus lineage among the 20 genes with highest correlation (Fig. 4e): Sfn and Perp are part of the p53 signaling pathway controlling murine mTEC differentiation44,45; additionally, the TF p63 targets Perp and is involved in murine mTEC differentiation46,47. Similarly, we recovered previously reported markers of murine mTECs, including Grhl3, Pvrl4 and Cd9 (ref. 37,48). In addition to these known markers of mTECs in mice, our top-ranked genes also included S100a11 and Fxyd3, markers of mTEC subpopulations in different human settings45,49,50,51,52, and Hspb1, a marker of later-stage murine mTECs53. Notably, the original study of our dataset identified the TF Grhl3 as a putative early mTEC marker with higher specificity compared to markers traditionally used.
为了解析导致髓质胸腺上皮细胞(一种与胸腺黏附相关的基质细胞类型 43 )的发育轨迹,我们首先选取了甲状旁腺、后鳃体、髓质及皮质胸腺上皮细胞(mTECs 与 cTECs)及其祖细胞亚群(扩展数据图 8c 和方法)。我们成功重建了初始状态(扩展数据图 8c)及各终末状态,相较于依赖 RNA 速率估计的结果获得了更高的 TSI 指标(TSI=1.0 对比 TSI=0.91;扩展数据图 8d)。通过计算向终末状态的命运概率,我们发现一个祖细胞簇具有更高的 mTEC 命运倾向(图 4e 和扩展数据图 9a,b)。这个潜在的 mTEC 祖先细胞簇在二维均匀流形近似与投影(UMAP)降维图中容易被忽略,凸显了我们高维命运分析的重要性(扩展数据图 9c)。随后,我们采用基于相关性的分析方法鉴定这一命运决定的潜在驱动因子,在相关性最高的 20 个基因中发现了转录因子(Fos、Grhl3 和 Elf5)及与胸腺谱系相关的基因(图... 4e):Sfn 和 Perp 是控制小鼠 mTEC 分化的 p53 信号通路的一部分 44,45 ;此外,转录因子 p63 靶向 Perp 并参与小鼠 mTEC 分化 46,47 。同样,我们找回了先前报道的小鼠 mTEC 标志物,包括 Grhl3、Pvrl4 和 Cd9(参考文献 37,48 )。除了这些已知的小鼠 mTEC 标志物外,我们排名靠前的基因还包括 S100a11 和 Fxyd3,这些是不同人类环境中 mTEC 亚群的标志物 45,49,50,51,52 ,以及 Hspb1,这是后期小鼠 mTEC 的标志物 53 。值得注意的是,对我们数据集的原始研究确定转录因子 Grhl3 是一个假定的早期 mTEC 标志物,与传统使用的标志物相比具有更高的特异性。
Unlike CellRank 2, WOT relies solely on inter-time-point information. Applied to the pharyngeal endoderm data, it failed to identify the putative mTEC ancestor cluster. Additionally, even when we leveraged the knowledge of putative mTEC progenitors identified by the RealTimeKernel at the earlier experimental time points, classical WOT identified fewer driver gene candidates with known functions in mTEC development at these time points (Fig. 4f and Extended Data Fig. 9d,e). We speculate that this decrease in performance is caused by WOT relying on pullback distributions, which assign a likelihood to each early-day cell to differentiate into any late-day cell but do not take intra-time point dynamics into account. In contrast, CellRank 2 computes continuous fate probabilities with a global transition matrix, combining transitions within and across time points (Methods). Finally, classical differential expression testing also recovered fewer known driver genes and TFs as our correlation-based analysis (Extended Data Fig. 9f).
与 CellRank 2 不同,WOT 仅依赖时间点间的信息。将其应用于咽内胚层数据时,该方法未能识别出假定的 mTEC 祖先细胞群。此外,即使我们利用 RealTimeKernel 在早期实验时间点识别的假定 mTEC 祖细胞信息,经典 WOT 在这些时间点鉴定出的 mTEC 发育相关驱动基因候选数量仍较少(图 4f 和扩展数据图 9d,e)。我们推测这种性能下降是由于 WOT 依赖回拉分布——该分布虽能计算早期细胞分化为任意晚期细胞的概率,但未考虑时间点内的动态变化。相比之下,CellRank 2 通过全局转移矩阵计算连续命运概率,整合了时间点内和跨时间点的转移过程(方法部分)。最后,经典差异表达分析鉴定的已知驱动基因和转录因子数量也少于我们基于相关性的分析(扩展数据图 9f)。
Our RealTimeKernel incorporates gene expression changes within and across experimental time points. Notably, these complementary views allowed identifying a putative progenitor population and substantially more relevant drivers compared to approaches focusing on a single data view.
我们的 RealTimeKernel 整合了实验时间点内及跨时间点的基因表达变化。值得注意的是,与专注于单一数据视图的方法相比,这些互补视角能识别出假定的祖细胞群和显著更多相关驱动因素。
Estimating kinetic rates and fate from metabolic labels
通过代谢标记估算动力学速率与细胞命运
The destructive nature of standard single-cell protocols prohibits directly examining gene expression changes over time. Metabolic labeling of newly transcribed mRNA molecules9,11,12,31; however, yields time-resolved single-cell RNA measurements that should substantially improve our ability to learn system dynamics. The temporal resolution is in the order of minutes to hours and thus much finer compared to typical time-course studies. We developed an approach to learn directed state-change trajectories from metabolic-labeling data using pulse–chase experiments (Fig. 5a and Methods).
标准单细胞协议的破坏性本质阻碍了直接观测基因表达的时序变化。然而,对新转录 mRNA 分子进行代谢标记 9,11,12,31 ,可获得时间分辨的单细胞 RNA 测量数据,这将极大提升我们学习系统动态的能力。其时间分辨率在分钟至小时量级,相比典型时间序列研究精细得多。我们开发了一种利用脉冲追踪实验从代谢标记数据中学习有向状态变化轨迹的方法(图 5a 及方法部分)。
图 5:通过代谢标记量化谱系特异性调控策略
a, Cells are metabolically labeled in pulse–chase experiments9 followed by simultaneous sequencing. Pulse experiments involve incubation with nucleoside analogs for varying durations; in chase experiments, cellular mRNA fully incorporates nucleoside analogs during a long incubation, followed by washing out of these nucleosides for varying durations. b, For each cell, gene and labeling duration, we identify the number of neighbors such that a predefined number of cells with non-trivial counts are included in the neighborhood, illustrated here for an exemplary cell A. These cells are then used to estimate cell and gene-specific transcription and degradation rates α and γ, respectively, to model the dynamics of labeled mRNA. c, UMAP embedding highlighting terminal states identified using CellRank 2 and dynamo. Green ticks indicate that a method recovered the corresponding terminal state, and red crosses indicate that the terminal state was not identified. d, Ranking of drivers for each lineage identified by different methods. Dynamo identified only enterocytes as terminal and, thus, provides a gene ranking only for this lineage. For dynamo, the mean gene ranking and corresponding 95% confidence band are shown (Methods). e, Inferred transcription (left) and degradation (right) rates of top-ranked known drivers of the goblet lineage. f, Same as e, but along the enterocyte lineage.
a、细胞在脉冲-追踪实验中进行代谢标记 9 ,随后进行同步测序。脉冲实验涉及用核苷类似物孵育不同时长;在追踪实验中,细胞 mRNA 在长时间孵育期间完全掺入核苷类似物,随后通过不同时长的洗脱去除这些核苷。b、对于每个细胞、基因和标记时长,我们确定邻域内包含预定数量非零计数细胞的邻居数量,此处以示例细胞 A 进行说明。这些细胞随后被用于分别估算细胞和基因特异的转录速率α与降解速率γ,以模拟标记 mRNA 的动态变化。c、UMAP 降维图突出显示使用 CellRank 2 和 dynamo 识别的终末状态。绿色勾号表示方法成功识别对应终末状态,红色叉号表示未识别该终末状态。d、不同方法对各谱系驱动基因的排序结果。Dynamo 仅将肠上皮细胞识别为终末状态,因此仅提供该谱系的基因排序。 对于 dynamo,展示了平均基因排名及相应的 95%置信区间(方法部分)。e,杯状细胞谱系中排名靠前的已知驱动因子的推断转录速率(左)和降解速率(右)。f,与 e 相同,但针对肠上皮细胞谱系。
Similar to previous approaches9, we model mRNA dynamics through a dynamical system, including mRNA molecule transcription and degradation rates9. We estimate these rates for each cell and gene by considering the dynamical information conveyed through metabolic labels (Fig. 5b and Methods). Based on a cell–cell similarity graph, for each cell, gene and labeling time, we identify a neighborhood in which a sufficient number of cells express the given gene. Next, we estimate transcription and degradation rates based on these cell sets by minimizing the squared Euclidean distance between observed and estimated transcripts. With these parameters, we infer a high-dimensional velocity vector field used to obtain cell–cell transition probabilities with the VelocityKernel.
与先前方法 9 类似,我们通过动态系统(包括 mRNA 分子转录和降解速率 9 )对 mRNA 动态进行建模。通过代谢标签传递的动态信息(图 5b 和方法部分),我们为每个细胞和基因估计这些速率。基于细胞-细胞相似性图,对于每个细胞、基因和标记时间,我们确定一个足够数量细胞表达给定基因的邻域。接着,通过最小化观测与估计转录本之间的欧几里得距离平方,基于这些细胞集估计转录和降解速率。利用这些参数,我们推断出一个高维速度矢量场,用于通过 VelocityKernel 获取细胞间转移概率。
We applied our devised method to data from murine intestinal organoids labeled with scEU-seq9, focusing on the enterocyte, enteroendocrine, goblet and paneth lineages (Extended Data Fig. 10a and Methods). Following parameter estimation, we computed the underlying velocity field, inferred transition probabilities and recovered all four terminal states (Fig. 5c). Similarly, we recovered all four terminal states using classical RNA velocity with the VelocityKernel, that is, using CellRank 1 (Extended Data Fig. 10b). We assessed the quality of inferred terminal states via cell-type purity, defined as the percentage of the most abundant cell type, reasoning that a high cell-type purity results from a low inference uncertainty of the underlying transition matrix (Methods). Indeed, we observed a high cell-type purity (85% on average) for each terminal state using the velocity field derived from the metabolic-labeling information but lower cell-type purity (67% on average) when relying on classical RNA velocity estimates (Extended Data Fig. 10c). Additionally, CellRank 2 outperformed CellRank 1 in terms of the TSI score (TSI = 0.81 and TSI = 0.71, respectively; Extended Data Fig. 10d).
我们将开发的方法应用于 scEU-seq 标记的小鼠肠道类器官数据 9 ,重点关注肠上皮细胞、肠内分泌细胞、杯状细胞和潘氏细胞谱系(扩展数据图 10a 及方法部分)。完成参数估计后,我们计算了底层速度场,推断出转移概率并成功识别出全部四种终末状态(图 5c)。同样地,使用 VelocityKernel 的经典 RNA 速度分析(即 CellRank 1)也成功识别了全部四种终末状态(扩展数据图 10b)。我们通过细胞类型纯度(定义为最丰富细胞类型的占比百分比)评估推断终末状态的质量,其理论依据是:高细胞类型纯度源于底层转移矩阵的低推断不确定性(方法部分)。事实上,利用代谢标记信息推导的速度场对每个终末状态都观测到高细胞类型纯度(平均 85%),而依赖经典 RNA 速度估计时纯度较低(平均 67%)(扩展数据图 10c)。此外,CellRank 2 在 TSI 评分上优于 CellRank 1(分别为 TSI=0.81 和 TSI=0.71;扩展数据图 10d)。
We compared our approach with dynamo16, an alternative method for estimating cellular dynamics based on metabolic-labeling data. In contrast to our approach, dynamo relies on a steady-state assumption, only uses a small subset of cells for parameter inference, does not estimate cell-specific rates and infers cellular trajectories deterministically. Applied to the organoid data, dynamo only recovered the enterocyte population as a terminal state (Fig. 5c, Extended Data Fig. 10e and Methods).
我们将自己的方法与 dynamo 16 进行了比较,后者是一种基于代谢标记数据估计细胞动力学的替代方法。与我们的方法不同,dynamo 依赖于稳态假设,仅使用一小部分细胞进行参数推断,不估计细胞特异性速率,并以确定性方式推断细胞轨迹。应用于类器官数据时,dynamo 仅将肠上皮细胞群识别为终末状态(图 5c、扩展数据图 10e 及方法部分)。
Beyond identifying the most mature cell population in each lineage, we asked whether our approach ranked known lineage drivers higher than competing approaches that do incorporate labeling information (dynamo) or that do not (CellRank 1 with scVelo’s dynamical model of RNA velocity and a random baseline). To assess the quality of each method’s gene ranking, we curated an optimally ranked list of known regulators and markers54 of each lineage and compared each method’s ranking to it (Methods). As dynamo only identified enterocytes as a terminal cluster, it could not rank drivers of any other lineage. Using CellRank 2 based on labeling information achieved the best ranking for each of the four terminal states (Fig. 5d and Extended Data Fig. 10f) and notably outperformed competing approaches, including CellRank 1, both when correlating gene expression and the inferred transcription rates with fate probabilities to identify putative driver genes.
除了识别每个谱系中最成熟的细胞群体外,我们还探究了本方法是否比那些整合标记信息的竞争方法(如 dynamo)或不整合标记信息的方法(如基于 scVelo RNA 速率动力学模型的 CellRank 1 及随机基线)更能优先排列已知谱系驱动因子。为评估各方法基因排序的质量,我们整理了每个谱系已知调控因子和标记物 54 的最优排序列表,并将各方法的排序与之对比(方法部分)。由于 dynamo 仅将肠上皮细胞识别为终末集群,无法对其他谱系的驱动因子进行排序。基于标记信息的 CellRank 2 在所有四个终末状态中均实现了最佳排序(图 5d 和扩展数据图 10f),且在通过关联基因表达与推断转录速率来识别潜在驱动基因时,其命运概率相关性显著优于包括 CellRank 1 在内的竞争方法。
The estimated cell- and gene-specific kinetic rates enabled us to investigate how these lineage-correlated genes are regulated by mRNA transcription and degradation. Analyzing the regulatory strategies of known markers and regulators ranked among the top 100 lineage-correlated genes for the goblet lineage revealed two different regulatory strategies (Fig. 5e). The first strategy increases transcription rates with decreasing degradation rates (for example, Spdef, Sytl2 and Fcgbp) and the second simultaneously increases transcription and degradation rates (for example, Atp2a3, Tff3 and Rassf6); both align with earlier findings of cooperative (case 1) and destructive (case 2) regulation strategies9. Although it is so far not possible to directly measure transcription and degradation rates in single-cell sequencing protocols, the increase in transcription rate aligns with the role of these genes as regulators and markers of the goblet lineage54. Similarly, in the enterocyte lineage, this same set of genes predominantly exhibits either (1) a decreased transcription accompanied by an increase in degradation rate (cooperative) or (2) an increase/decrease of both rates (destructive; Fig. 5f).
通过估计细胞和基因特异性的动力学速率,我们得以研究这些与谱系相关的基因如何受到 mRNA 转录和降解的调控。对杯状细胞谱系中排名前 100 的已知标记物和调控因子进行调控策略分析,揭示了两种不同的调控模式(图 5e)。第一种策略在转录速率上升的同时降低降解速率(例如 Spdef、Sytl2 和 Fcgbp),第二种则同步提升转录与降解速率(例如 Atp2a3、Tff3 和 Rassf6);这两种模式均与此前发现的协同调控(情况 1)和破坏性调控(情况 2)策略相符 9 。尽管目前尚无法在单细胞测序方案中直接测量转录和降解速率,但转录速率的提升与这些基因作为杯状细胞谱系调控因子和标记物的功能相一致 54 。 同样地,在肠上皮细胞谱系中,这组基因主要表现出以下两种模式:(1) 转录水平下降伴随降解速率上升(协同作用)或 (2) 两种速率同时上升/下降(拮抗作用;图 5f)。
Discussion 讨论
CellRank 2 is a robust, modular and scalable framework to infer and study single-cell trajectories and fate decisions. By separating the inference and analysis of transition matrices via kernels and estimators, respectively, CellRank 2 accommodates diverse data modalities and overcomes the limitations of single data-type approaches in a consistent and unified manner. Our tool successfully performed pseudotime-based analysis of human hematopoiesis and deciphered gene dynamics during human endoderm development using stemness estimates. Notably, the modular and scalable design facilitated the rapid integration of each data modality and allowed CellRank 2 to analyze much larger datasets compared to previous approaches and implementations.
CellRank 2 是一个稳健、模块化且可扩展的框架,用于推断和研究单细胞轨迹及命运决策。通过分别利用核函数和估计器分离转移矩阵的推断与分析,CellRank 2 以一致且统一的方式适应多种数据模态,克服了单一数据类型方法的局限性。我们的工具成功基于拟时序分析了人类造血过程,并利用干性估计解读了人类内胚层发育期间的基因动态。值得注意的是,模块化和可扩展的设计促进了每种数据模态的快速整合,使 CellRank 2 能够分析比以往方法和实现更大的数据集。
Developing an efficient OT-based kernel allowed us to integrate time-series data, considering both inter- and intra-time point information. With this formulation, we identified a putative progenitor population of medullary thymic epithelial cells missed by methods that ignore dynamics within time points. Recently, time-course studies have been combined with genetic lineage tracing55,56,57,58 or spatial resolution59,60,61 and emerging computational methods21,22,23,24 use this information to map cells more faithfully across time. These enhanced inter-time point mappings can be used with our RealTimeKernel for further analysis, as demonstrated for lineage-traced Caenorhabditis elegans data in moslin23 and spatiotemporal mouse embryogenesis data in moscot24. These applications highlight the importance of our view-agnostic framework for analyzing increasingly large, complex and multi-modal time-course studies. Additionally, Mellon62, a recently proposed alternative approach for continuous analysis of time-course data, could improve our mappings by incorporating their density estimates in the OT problem.
开发一种基于最优传输(OT)的高效核使我们能够整合时间序列数据,同时考虑时间点间和时间点内的信息。通过这一方法,我们识别出一个被忽略时间点内动态的方法所遗漏的髓质胸腺上皮细胞潜在祖细胞群。近期研究已将时间进程实验与遗传谱系追踪 55,56,57,58 或空间分辨率 59,60,61 相结合,新兴计算方法 21,22,23,24 利用这些信息实现更准确的跨时间细胞映射。这些强化的时间点间映射可与我们的 RealTimeKernel 结合进行深入分析,如在线虫谱系追踪数据(moslin 23 )和小鼠胚胎发育时空数据(moscot 24 )中的应用所示。这些案例凸显了我们视角无关框架对于分析日益庞大、复杂且多模态的时间进程研究的重要性。此外,新近提出的 Mellon 62 方法——一种用于时间序列数据连续分析的替代方案——可通过将其密度估计纳入 OT 问题来优化我们的映射结果。
Our kernel-estimator design proved particularly valuable when integrating metabolic labeling to estimate cell-specific mRNA transcription and degradation rates. We demonstrated the ability of metabolic-labeling data to overcome the intrinsic limitations of splicing-based velocity inference by successfully identifying all lineages in gut organoid differentiation. Combining the inferred kinetic rates with CellRank 2 also makes it possible to study gene regulatory strategies underlying cellular state changes, as we showed for the goblet and enterocyte lineages. Parallel to our approach, others developed velvet63 and storm64 to estimate cellular dynamics from metabolic-labeling data; however, compared to our approach, velvet does not estimate transcription rates and assumes constant degradation rates across all cells. While storm relaxes this assumption, it does so only through post-processing steps. Additionally, storm relies on deterministic downstream analyses. In contrast, CellRank 2 estimates cell-specific transcription and degradation rates and offers probabilistic downstream analysis through flexible Markov-chain modeling.
我们的核估计器设计在整合代谢标记以估算细胞特异性 mRNA 转录和降解速率时展现出独特价值。通过成功识别肠道类器官分化中的所有谱系,我们证明了代谢标记数据能够克服基于剪接的速率推断的固有局限性。将推断的动力学速率与 CellRank 2 相结合,还能研究细胞状态变化背后的基因调控策略,如我们在杯状细胞和肠上皮细胞谱系中所展示的。与我们的方法并行,其他团队开发了 velvet 63 和 storm 64 来从代谢标记数据估计细胞动态;然而相比我们的方法,velvet 不估计转录速率且假设所有细胞的降解速率恒定。虽然 storm 放宽了这一假设,但仅通过后处理步骤实现。此外,storm 依赖于确定性的下游分析。相比之下,CellRank 2 能估计细胞特异性转录和降解速率,并通过灵活的马尔可夫链建模提供概率性下游分析。
Recent experimental advances combine single-cell metabolic-labeling techniques with droplet-based assays11,65 or split-pool barcoding approaches10,63 to label transcripts at atlas scale and demonstrate metabolic labeling for in vivo systems66 and in the context of spatially resolved assays13, underscoring the need for scalable analytical approaches as proposed in this study. We aim to expand our framework further by simultaneously inferring kinetic rates and ordering cells along differentiation trajectories.
最近的实验进展将单细胞代谢标记技术与基于液滴的检测方法 11,65 或分池条形码方法 10,63 相结合,实现了图谱规模的转录本标记,并在体内系统 66 和空间分辨检测环境 13 中验证了代谢标记技术的适用性,这凸显了如本研究所提出的可扩展分析方法的重要性。我们的目标是通过同时推断动力学速率和沿分化轨迹对细胞进行排序,进一步扩展我们的框架。
We have introduced kernels that make use of different types of directional information of cellular state changes (Extended Data Fig. 1). If metabolic labels from pulse (chase) experiments for at least two (three) labeling durations are available, our proposed method to infer a metabolic-labeling informed vector field is suitable. The RealTimeKernel is applicable for time series in which time points are closely spaced with respect to the underlying dynamical process. The VelocityKernel can be used with RNA velocity for systems that meet the assumptions of RNA velocity inference methods67,68. Finally, the PseudotimeKernel can enhance the understanding of cellular state changes if a unique initial state is identifiable and differentiation proceeds unidirectionally, and the CytoTRACEKernel can be used when the initial state is unknown. Notably, the proposed kernels lead to different results if the underlying assumptions are violated or not sufficiently satisfied (Supplementary Note 1). For example, the VelocityKernel failed to faithfully recapitulate the known differentiation hierarchy of hematopoiesis due to unsatisfied assumptions of the RNA velocity model. Different kernels can be combined with user-defined global weights if multiple criteria are met, as we demonstrated for the RealTimeKernel; other studies used CellRank 2’s kernel combinations to study the developmental processes in epicardioids69 and to reveal the developmental history during human cortical gyrification70, for example. In the future, we plan to introduce local kernel combinations that would involve kernel weights based on the relative position of cells within the phenotypic manifold, allowing for context-dependent integration of multiple data sources.
我们引入了利用细胞状态变化不同类型方向性信息的核函数(扩展数据图 1)。若脉冲(追踪)实验中至少两个(三个)标记时长的代谢标记数据可用,我们提出的代谢标记信息向量场推断方法将适用。RealTimeKernel 适用于时间点相对于底层动力学过程紧密排列的时间序列数据。VelocityKernel 可与满足 RNA 速度推断方法假设条件的系统 67,68 的 RNA 速度数据联用。当可识别唯一初始状态且分化过程呈单向性时,PseudotimeKernel 能增强对细胞状态变化的理解;而初始状态未知时可采用 CytoTRACEKernel。值得注意的是,若底层假设被违背或未充分满足,所提出的核函数会产生不同结果(补充说明 1)。例如由于 RNA 速度模型的假设未满足,VelocityKernel 未能真实重现已知的造血分化层次结构。 如果满足多个条件,不同内核可以与用户定义的全局权重结合使用,正如我们在 RealTimeKernel 中所演示的;例如,其他研究利用 CellRank 2 的内核组合研究了心外膜类器官的发育过程 69 ,并揭示了人类大脑皮层沟回形成过程中的发育历史 70 。未来,我们计划引入局部内核组合,这将涉及基于细胞在表型流形中相对位置的内核权重,从而实现对多数据源的上下文依赖性整合。
Identifying putative driver genes is another aspect that can be extended in future work. Currently, we rank putative driver genes by correlating fate probabilities with gene expression. Although this approach has proven powerful, as shown in various applications, it is solely based on correlation. To unravel the causal mechanisms linking molecular properties and changes to fate decisions, perturbation data and causal inference71 can be combined with CellRank 2. This combination will ultimately enhance our understanding of underlying molecular drivers. Overall, we anticipate our framework to be crucial in understanding and conceptualizing fate choice as single-cell datasets grow in scale and diversity.
识别潜在的驱动基因是未来工作中可以扩展的另一个方面。目前,我们通过将命运概率与基因表达相关联来对潜在驱动基因进行排序。尽管这种方法在各种应用中已证明其强大性,但它仅基于相关性。为了揭示分子特性与命运决策变化之间的因果机制,可将扰动数据和因果推断 71 与 CellRank 2 相结合。这种结合最终将增强我们对潜在分子驱动因素的理解。总体而言,随着单细胞数据集规模和多样性的增长,我们预计该框架将在理解和概念化命运选择方面发挥关键作用。
Methods 方法
CellRank 2: a unified framework to probabilistically model cellular state changes
CellRank 2:概率建模细胞状态变化的统一框架
To overcome the inherent limitations of RNA velocity and unify TI across different data views, we developed CellRank 2; our framework describes cellular dynamics probabilistically, as proposed in our earlier work14. Specifically, we introduced the first probabilistic modeling framework that automatically determines the direction of cellular state changes to extend TI beyond normal development. Generalizing this paradigm to different biological priors and guaranteeing applicability in many scenarios required us to rethink the CellRank structure entirely. To this end, we base our new version on three key principles:
为克服 RNA 速率的固有局限并统一不同数据视角下的轨迹推断,我们开发了 CellRank 2;该框架如我们早期工作 14 所述,以概率方式描述细胞动态。具体而言,我们首次提出了能自动判定细胞状态变化方向的概率建模框架,将轨迹推断扩展到正常发育之外。为使该范式适用于不同生物学先验并确保多场景通用性,我们彻底重构了 CellRank 体系。新版框架基于三大核心原则:
-
1.
Robustness: fate restriction is a gradual, noisy process requiring probabilistic treatment. Therefore, we use Markov chains to describe stochastic fate transitions, with each state of the Markov chain representing one cell.
稳健性:命运限制是一个渐进且充满噪声的过程,需要概率化处理。因此,我们使用马尔可夫链来描述随机的命运转换,其中马尔可夫链的每个状态代表一个细胞。 -
2.
Modularity: quantifying transition probabilities between cells is independent of analyzing them. Thus, we modularized the CellRank framework into kernels to compute transition probabilities and estimators to analyze transition probabilities. This structure guarantees flexibility in applications and is easily extensible.
模块化设计:量化细胞间转移概率与分析过程相互独立。因此,我们将 CellRank 框架模块化为计算转移概率的内核与分析转移概率的估计器。这种结构确保了应用的灵活性,并易于扩展。 -
3.
Scalability: we assume each cell can transition into a small set of possible descendant states. Consequently, transition matrices are sparse, and computations scale to vast cell numbers (Extended Data Fig. 2).
可扩展性:假设每个细胞仅能向少量可能的后代状态转变,因此转移矩阵具有稀疏性,计算可适应海量细胞规模(扩展数据图 2)。
Innovations in CellRank 2
CellRank 2 的创新突破
Our design principles allowed us to improve our original work in three major aspects:
我们的设计原则促使原始工作在三大方面实现提升:
-
1.
We design a modular interface that allows us to decouple the construction of a Markov chain from the process of formulating a hypothesis based on the Markov chain.
我们设计了一个模块化接口,使得马尔可夫链的构建过程能够与基于该链提出假设的过程解耦。 -
2.
We introduce the PseudotimeKernel, CytoTRACEKernel and RealTimeKernel, as well as a method to infer kinetic rates from metabolic-labeling data, to render CellRank 2 applicable beyond RNA velocity; we do so by using a pseudotime, a measure of developmental potential, time-course data and metabolic-labeling information, respectively.
我们引入了伪时序核、CytoTRACE 核和实时核,以及从代谢标记数据推断动力学速率的方法,从而让 CellRank 2 的应用范围超越 RNA 速率;具体实现手段分别是利用伪时序、发育潜能度量指标、时间序列数据和代谢标记信息。 -
3.
We make our framework faster by accelerating our main estimator by one order of magnitude, easier to use by refactoring our codebase and more interpretable by visualizing kernel dynamics via random walks.
我们通过将主估算器速度提升一个数量级来加速框架运行,通过重构代码库提升易用性,并通过随机游走可视化核动力学来增强可解释性。
Key outputs of CellRank 2
CellRank 2 的核心输出
Although inputs to CellRank 2 are kernel-dependent (Extended Data Fig. 1), outputs are consistent across all kernels:
尽管 CellRank 2 的输入依赖于内核(扩展数据图 1),但所有内核的输出保持一致:
-
Initial, intermediate and terminal states of cellular trajectories.
细胞轨迹的初始、中间和终末状态。 -
Fate probabilities, quantifying how likely each cell is to reach each terminal (or intermediate) state.
命运概率,量化每个细胞到达每个终末(或中间)状态的可能性。 -
Gene expression trends specific to each identified trajectory.
每条已识别轨迹特有的基因表达趋势。 -
Putative driver genes of fate decisions through correlating gene expression with fate probability.
通过基因表达与命运概率的关联分析,识别命运决策的潜在驱动基因。 -
Dedicated visualization tools for all key outputs, for example, circular embeddings for fate probabilities, heatmaps for cascades of trajectory-specific gene expression and line plots for gene trends along different trajectories.
针对所有关键输出的专用可视化工具,例如:用环形嵌入展示命运概率、热图呈现轨迹特异性基因表达的级联效应、折线图显示不同轨迹上的基因趋势。
A conceptual overview of kernels in CellRank 2
CellRank 2 中核函数的概念性概述
Decoupling inference of transition probability from their analysis
将转移概率的推断与其分析解耦
The typical CellRank 2 workflow consists of two steps: (1) estimating cell–cell transition probabilities and (2) deriving biological insights based on these estimates. Previously, we tied these two steps together14 but realized that decoupling them yields a much more powerful and flexible modeling framework. Treating each step separately is possible as analyzing transition matrices is independent of their construction. For example, estimating transition probabilities based on RNA velocity or a pseudotime does not change how initial and terminal states are inferred or fate probabilities estimated. Consequently, modularizing our problem-specific framework generalizes the corresponding analysis tools to other data modalities. The two steps of our inference workflow are conceptualized by kernels and estimators, respectively.
CellRank 2 的标准工作流程包含两个步骤:(1)估计细胞间转移概率;(2)基于这些估计值推导生物学洞见。先前我们将这两个步骤紧密耦合 14 ,但后来意识到解耦它们能构建更强大灵活的建模框架。由于转移矩阵的分析独立于其构建过程,因此可以分别处理每个步骤。例如,基于 RNA 速度或伪时间估计转移概率,并不会改变初始态与终末态的推断方式或命运概率的估算方法。因此,将我们这个针对特定问题的框架模块化后,相应的分析工具便可推广至其他数据模态。我们的推断工作流程通过核函数和估计器分别实现这两个步骤的概念化。
Kernels estimate transition matrices at a cellular resolution with nc denoting the number of cells; row Tj,: represents the transition probabilities of cell j toward putative descendants. With CellRank 2, we provide means to quantify fate probabilities based on RNA velocity (VelocityKernel), pseudotime (PseudotimeKernel), a developmental potential (CytoTRACEKernel), experimental time points (RealTimeKernel) and metabolic labeling (metabolic-labeling-based vector field with the VelocityKernel).
核函数以细胞分辨率估计转移矩阵 \(T\in }^\times {n}_{\rm{c}}}\),其中 n c 表示细胞数量;矩阵行 T j,: 表示细胞向假定后代的转移概率。通过 CellRank 2,我们提供了基于 RNA 速率(VelocityKernel)、伪时间(PseudotimeKernel)、发育潜能(CytoTRACEKernel)、实验时间点(RealTimeKernel)以及代谢标记(基于代谢标记的矢量场与 VelocityKernel 结合)来量化命运概率的方法。
Initial state identification
初始状态识别
Kernel-derived transition matrices quantify probabilities of cell transitions to putative progenitor states. To estimate initial states, instead, we work with the transposed transition matrix, thereby quantifying transition probabilities from progenitor cells to their putative ancestors. Each kernel automatically row-normalizes the transposed transition matrix.
核导出的转移矩阵量化了细胞向假定祖细胞状态转变的概率。为估计初始状态,我们转而使用转置后的转移矩阵,从而量化从祖细胞到其假定祖先细胞的转移概率。每个核函数会自动对转置后的转移矩阵进行行归一化处理。
Kernel combination 内核组合
Different data modalities may capture different aspects of biological processes. To take advantage of multiple data modalities, kernels can be combined to quantify the likely state change in a single, aggregated transition matrix. Consider two kernels k(1) and k(2) with corresponding transition matrices T(1) and T(2), respectively. CellRank 2 allows combining the two kernels into a joint kernel k defined as k = αk(1) + (1 − α)k(2) with a weight parameter α ∈ [0, 1]. The corresponding normalized transition matrix T is computed automatically and is thus, given by
不同数据模态可能捕捉生物过程的不同方面。为利用多模态数据优势,可通过组合核函数在单一聚合转移矩阵中量化可能的状态变化。设有两个核函数 k (1) 和 k (2) ,其对应转移矩阵分别为 T (1) 和 T (2) 。CellRank 2 允许将这两个核函数合并为联合核函数 k,定义为 k = αk (1) + (1 − α)k (2) ,其中权重参数α ∈ [0, 1]。对应的归一化转移矩阵 T 将自动计算得出,其表达式为
The terminal state identification score for kernel comparison
用于核函数比较的终态识别评分
If terminal states of the studied system are known a priori, kernels can be compared by considering how well the kernels identify terminal states with an increasing number of macrostates; an optimal strategy identifies a new terminal state with every added macrostate until all terminal states have been identified. We summarize the performance of an arbitrary kernel relative to such an optimal identification with the TSI score: consider a system containing m terminal states and the function f that assigns each number of macrostates n the corresponding number of identified terminal states. In the case of a strategy that identifies terminal states optimally, fopt describes the step function
如果所研究系统的终末状态已知,可以通过考察核函数在增加宏观状态数量时识别终末状态的能力来比较不同核函数;最优策略会在每增加一个宏观状态时识别出一个新的终末状态,直至所有终末状态都被识别。我们通过 TSI 评分来总结任意核函数相对于这种最优识别的性能:考虑一个包含 m 个终末状态的系统,以及将每个宏观状态数量 n 映射到相应已识别终末状态数量的函数 f。对于最优识别终末状态的策略而言,f opt 描述的是阶跃函数。
We define the TSI score for an arbitrary kernel κ as the area under the curve fκ relative to the area under the curve fopt, that is
我们将任意核κ的 TSI 分数定义为曲线 f κ 下方面积相对于曲线 f opt 下方面积的比值,即
with maximum number of macrostates assessed Nmax.
其中 N max 表示评估的宏观状态最大数量。
Kernel comparison via the cross-boundary correctness score
通过跨边界正确性分数进行核比较
While the CellRank 2 framework aims at quantifying cell trajectories, correct transitions between coarse cell states, such as cell types, are sometimes known a priori. In such cases, the CBC score29 can be used to compare two kernels: Consider two cell states and , where is a progenitor state of , a precomputed nearest-neighbor graph with weights wjk between observations j and k and denote the neighborhood of observation j by . The representation of observation j is denoted by xj; all cell representations are collected in the matrix X. We define the boundary of to as all cells with at least one neighbor in and denote it by , that is
虽然 CellRank 2 框架旨在量化细胞轨迹,但粗粒度细胞状态(如细胞类型)间的正确转换有时是已知先验的。在此情况下,可使用 CBC 评分 29 来比较两个核函数:考虑两个细胞状态\(C_{1}\)和\(C_{2}\),其中\(C_{2}\)是\(C_{1}\)的祖细胞状态,预计算的最近邻图在观测值间具有权重 w jk ,k 表示观测值的邻域,记作\(N(j\,)\)。观测值的表征记为 x;所有细胞表征收集于矩阵 X 中。我们将\(C_{1}\)到\(C_{2}\)的边界定义为至少有一个邻居在\(C_{2}\)中的所有细胞,记作\({\partial }_{1\to 2}C_{1}\),即
For every boundary cell, we empirically define the velocity v(j) of observation as
对于每个边界细胞,我们经验性地将观测 的速度 v()定义为
Similarly, for a given kernel κ, we estimate the velocity of observation j via
同样地,对于给定的核κ,我们通过观测估计其速度
where denotes the jth row of the transition matrix computed with kernel κ. The CBC score β(κ)(j) of cell j under kernel κ is then given by the Pearson correlation between v(j) and v(κ)(j).
其中 表示使用核κ计算的转移矩阵的第行。细胞在核κ下的 CBC 得分β (κ) ()由 v()和 v (κ) ()之间的皮尔逊相关性给出。
To compare two kernels κ1 and κ2, for each observation, we compute the log ratio of the corresponding CBC scores and . If the velocity estimate based on kernel κ1 aligns more with the empirical estimate, the log ratio is positive and negative otherwise. A one-sided Welch’s t-test can be used to test if kernel κ1 significantly outperforms kernel κ2.
为比较两个核函数κ 1 与κ 2 ,我们对每个观测值计算相应 CBC 分数 与 的对数比率。若基于核κ 1 的速度估计与经验估计更吻合,则对数比率为正,反之为负。可采用单侧韦尔奇 t 检验来验证核κ 1 是否显著优于核κ 2 。
Visualizing kernel dynamics: random walks and projections
核函数动态可视化:随机游走与投影
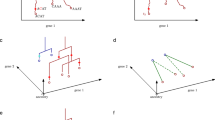
Although inferred transition probabilities are predominantly used for more in-depth data analyses based on estimators, we also provide means to visualize cellular dynamics directly based on the kernel output. These visualizations are intended to provide a preliminary understanding of the underlying dynamics and serve as a starting point for further analyses. Here, we enable studying the evolution of cellular state change either based on random walks in the high-dimensional gene expression space or a projection of the high-dimensional vector field onto a low-dimensional latent space representation of the data.
尽管推断的转移概率主要用于基于估计器的深入数据分析,我们也提供了直接基于核输出可视化细胞动态的方法。这些可视化旨在帮助初步理解潜在动态,并作为后续分析的起点。在此,我们支持通过高维基因表达空间中的随机游走,或将高维向量场投影到数据的低维潜在空间表示,来研究细胞状态变化的演化过程。
Transition matrices induce random walks modeling the evolution of individual cells. Given a cell j, we successively sample its future state k under the given transition matrix. Starting cells for random walks can be sampled either at random or from a user-defined early cell cluster. We terminate random walks when a predefined maximum number of steps has been performed or when a predefined set of terminal cells has been reached. By studying multiple random walks, the expected dynamics are revealed. Random walks, including their start and final cells, can then be visualized in a low-dimensional representation of the data. Within our framework, random walks are computed efficiently via a parallel implementation.
转移矩阵诱导随机游走,模拟单个细胞的演化过程。给定一个细胞,我们依据转移矩阵连续采样其未来状态 k。随机游走的起始细胞可从随机选择或用户指定的早期细胞簇中采样。当达到预设的最大步数或抵达预定义的终末细胞集时,随机游走终止。通过研究多重随机游走,可揭示预期动态。这些随机游走(包括其起始与终末细胞)可在数据的低维表征中进行可视化。在我们的框架中,随机游走通过并行计算实现高效运算。
Previously, the most popular approach for visualizing RNA velocity has been the projection of the high-dimensional vector field onto a low-dimensional latent space representation7. With CellRank 2, we generalize this concept to any kernel based on a k-nearest-neighbor graph, that is, the PseudotimeKernel, CytoTRACEKernel and VelocityKernel. The projection for a given cell is calculated as follows: Consider a transition matrix T, cell j with neighborhood and kj neighbors and latent representation zj. The projected velocity vj is then given by
此前,可视化 RNA 速率最常用的方法是将高维向量场投影到低维潜在空间表示 7 。通过 CellRank 2,我们将这一概念推广至任何基于 k 近邻图的核函数,即 PseudotimeKernel、CytoTRACEKernel 和 VelocityKernel。给定细胞的投影计算方式如下:考虑转移矩阵 T、具有邻域 和 k 个邻居的细胞及其潜在表示 z,其投影速度 v 的计算公式为
While we provide the option to visualize the projected velocity stream in low dimensions for specific kernels, we caution against the analysis thereof. Previous work7,72,73 highlighted how the projected velocity stream is sensitive to many parameters, including the gene set, the embedding technique and more (Supplementary Note 1). Instead, we encourage visualizing cellular dynamics through random walks, sampled independently of the embedding, or through initial and terminal states, fate probabilities and other quantities inferred in high dimensions through our estimator modules.
尽管我们提供了针对特定核函数在低维空间中可视化投影速度流的选项,但需谨慎分析此类结果。先前研究 7,72,73 指出,投影速度流对基因集、嵌入技术等诸多参数极为敏感(补充说明 1)。我们建议转而通过随机游走(采样过程独立于嵌入空间)或通过初始/终末状态、命运概率及估计器模块在高维空间推断的其他量化指标来呈现细胞动态。
A conceptual overview of estimators in CellRank 2
CellRank 2 中估计器的概念性概述
Based on transition matrices provided by kernels, we enable data-driven knowledge discovery. To this end, estimators first identify initial, intermediate and terminal states using the precomputed transition matrices. States are identified using concepts and results from the rich theory of Markov chains. Following this, we enable visualizing trajectory-specific gene expression trends and cascades of gene activation14, clustering expression trends14 or arranging cells in a circular embedding14,74 to summarize fate probabilities. We provide the necessary tools for each step of the downstream analysis as part of CellRank 2.
基于核函数提供的转移矩阵,我们实现了数据驱动的知识发现。为此,估计器首先利用预计算的转移矩阵识别初始态、中间态和终末态,其理论基础来自马尔可夫链的丰富理论与概念。随后,我们支持可视化轨迹特异性基因表达趋势和基因激活级联 14 、聚类表达趋势 14 ,或通过环形嵌入排列细胞 14,74 以总结命运概率。作为 CellRank 2 的组成部分,我们为下游分析的每个环节提供了必要工具。
The generalized Perron cluster cluster analysis estimator
广义 Perron 聚类分析估计器
As in our previous work, we compute macrostates and classify them as initial, intermediate and terminal by coarse-graining the cell–cell transition matrix. This approach is based on generalized Perron cluster cluster analysis19,20 (GPCCA), a method initially developed to study conformational protein dynamics.
延续先前工作,我们通过粗粒化细胞-细胞转移矩阵计算宏观状态,并将其分类为初始态、中间态和终末态。该方法基于广义 Perron 聚类分析 19,20 (GPCCA),该技术最初用于研究蛋白质构象动力学。
Performance improvements of CellRank 2
CellRank 2 的性能提升
Faster computation of fate probabilities
命运概率的更快计算
After estimating cell–cell transition probabilities through a kernel and identifying terminal states through an estimator, we assess cellular fate toward these terminal states. For each cell, we quantify its fate probability, that is, how likely it is to differentiate into one of the terminal states. Given our Markov-chain-based framework, fate probabilities can be computed in closed form using absorption probabilities; however, calculating absorption probabilities directly scales cubically in the number of cells. To overcome this computational burden, in our previous work, we reformulated the underlying problem as a set of linear systems. These linear systems are then solved in parallel using a sparsity-optimized iterative algorithm75; this reformulation scales near-linearly14.
在通过核函数估计细胞间转移概率并通过估计器识别终末状态后,我们评估细胞向这些终末状态的分化命运。对于每个细胞,我们量化其命运概率——即它分化成某一终末状态的可能性。基于我们的马尔可夫链框架,命运概率可通过吸收概率以闭式解形式计算;然而直接计算吸收概率的时间复杂度与细胞数量的三次方成正比。为克服这一计算负担,我们在先前工作中将基础问题重新表述为一组线性方程组,随后采用稀疏性优化的迭代算法 75 并行求解;这种重构方法具有近线性时间复杂度 14 。
Even though our previously proposed reformulation for computing absorption probabilities achieved a significant increase in performance compared to a naive implementation, we still encountered increased runtimes when analyzing larger datasets (Extended Data Fig. 2a). To reduce the runtime further, we devised an alternative but equivalent approach: Given a terminal state, we previously identified nf representative cells, computed absorption probabilities toward them, and aggregated them across the nf representative cells to assign a single, lineage-specific probability. In CellRank 2, we first combine the nf representative cells into a single pseudo-state and compute absorption probabilities toward it instead. While the corresponding results are mathematically equivalent, ignoring parallelization, this new approach is nf times faster. Therefore, with nf = 30 by default, our improved implementation results in a 30-fold speed-up.
尽管我们先前提出的吸收概率计算重构方案相比原始实现显著提升了性能,但在分析较大数据集时仍面临运行时间增加的问题(扩展数据图 2a)。为进一步缩短运行时间,我们设计了一种等效替代方案:给定终末状态时,原方案需识别 n 个代表细胞、计算针对它们的吸收概率,再通过 n 个代表细胞聚合得到单一谱系特异性概率;而在 CellRank 2 中,我们先将 n 个代表细胞合并为单个伪状态,直接计算针对该伪状态的吸收概率。在忽略并行化的情况下,虽然两种方案的数学结果等效,但新方案速度提升了 n 倍。默认设置 n=30 时,改进后的实现可获得 30 倍的加速效果。
Extensibility of CellRank 2
CellRank 2 的可扩展性
While we already provide multiple kernels tailored to different data modalities, current and future technologies provide additional sources of information. Concrete examples include spatially resolved time-course studies59,60,61 and genetic lineage-tracing data55,56,57,58, previously already integrated in the CellRank 2 ecosystem23,24. Our modular interface makes CellRank 2 easily extensible toward (1) alternative single-cell data modalities by including new kernels and (2) alternative trajectory descriptions generating different hypotheses through new estimators.
尽管我们已提供针对不同数据模态定制的多种核心算法,但当前及未来技术还将提供更多信息来源。具体实例包括空间分辨的时间序列研究 59,60,61 和遗传谱系追踪数据 55,56,57,58 ——这些已预先整合至 CellRank 2 生态系统 23,24 。我们的模块化接口使 CellRank 2 能轻松扩展至:(1)通过纳入新核心算法支持替代性单细胞数据模态;(2)通过新估计器生成不同假说的替代性轨迹描述。
The PseudotimeKernel: incorporating previous knowledge on differentiation
伪时序核心算法:整合分化过程的先验知识
Aligning cells along a continuous pseudotime mimicking the underlying differentiation process has been studied in many use cases. In particular, a pseudotime can be computed for systems where a single, known initial cellular state develops unidirectionally into a set of unknown terminal states. Based on the assigned pseudotime values, we quantify transition probabilities between cells using the PseudotimeKernel.
将细胞沿模拟潜在分化过程的连续伪时序排列已在众多应用场景中得到研究。特别是对于已知单一初始细胞状态单向发育为未知终末状态的系统,可计算其伪时序值。基于分配的伪时序值,我们使用伪时序核心算法量化细胞间的转移概率。
Given a similarity-based nearest-neighbor graph with a corresponding adjacency matrix , the PseudotimeKernel biases graph edges toward increasing pseudotime: consider a reference cell j, one of its neighbors k, the corresponding edge weight and the difference between their pseudotimes Δtjk. To favor cellular transitions toward increasing pseudotime, the PseudotimeKernel downweighs graph edges pointing into the reference cell’s pseudotemporal past while leaving the remaining edges unchanged. Edge weights are updated according to
给定一个基于相似性的最近邻图及其对应的邻接矩阵 ,伪时间核(PseudotimeKernel)会将图的边偏向于伪时间增加的方向:考虑一个参考细胞及其邻居 k,对应的边权重为 ,以及它们之间的伪时间差Δt jk 。为了促进细胞向伪时间增加的方向转变,伪时间核会降低指向参考细胞伪时间过去的边的权重,同时保持其余边的权重不变。边的权重根据以下规则进行更新:
with a function f implementing the thresholding scheme. In CellRank 2, we implement soft and hard thresholding. The soft scheme continuously downweighs edge weights according to
使用函数 f 实现阈值化方案。在 CellRank 2 中,我们实现了软阈值化和硬阈值化。软方案会根据...持续降低边权重
By default, the parameters b and ν are set to 10 and 0.5, respectively. This concept is similar to the scheme proposed by the TI method VIA25. In contrast to soft thresholds, hard thresholding follows a stricter policy inspired by Palantir5, discarding most edges that point into the pseudotemporal past.
默认情况下,参数 b 和ν分别设置为 10 和 0.5。这一概念类似于 TI 方法 VIA 25 提出的方案。与软阈值不同,硬阈值遵循受 Palantir 5 启发的更严格策略,会丢弃大部分指向伪时间过去的边。
The CytoTRACEKernel: inferring directionality from developmental potential
CytoTRACEKernel:从发育潜能推断方向性
CytoTRACE assigns each cell in a given dataset a developmental potential18. Score values range from 0 to 1, with 0 and 1 identifying mature and naive cells, respectively. Inverting the score, thus, defines a pseudotime for developmental datasets. In CellRank 2, the CytoTRACEKernel computes the CytoTRACE score and constructs the corresponding pseudotime to calculate a transition matrix as described for the PseudotimeKernel.
CytoTRACE 为给定数据集中的每个细胞分配发育潜能评分 18 。评分值范围从 0 到 1,其中 0 和 1 分别代表成熟细胞和初始细胞。通过反转该评分,可为发育数据集定义伪时序。在 CellRank 2 中,CytoTRACEKernel 通过计算 CytoTRACE 评分并构建相应伪时序来生成转移矩阵,其计算方式与 PseudotimeKernel 所述一致。
Adaptation of the CytoTRACE score
CytoTRACE 评分的适应性改进
When calculating the CytoTRACE score on larger datasets, we found the score construction either intractable due to long runtimes (40,000 to 80,000 cells) or failed to compute the score at all (more than 80,000 cells) (Extended Data Fig. 2b). Thus, to ensure computational efficiency when reconstructing the CytoTRACE score for larger datasets, we sought an alternative, computationally efficient and numerically highly correlated approach.
在大型数据集上计算 CytoTRACE 评分时,我们发现该评分构建过程要么因运行时间过长(40,000 至 80,000 个细胞)而难以处理,要么完全无法计算(超过 80,000 个细胞)(扩展数据图 2b)。因此,为确保在大型数据集上重建 CytoTRACE 评分时的计算效率,我们寻求了一种计算高效且数值高度相关的替代方案。
Conceptually, CytoTRACE proposes that the number of expressed genes decreases with cellular maturity. This assumption is biologically motivated by less-developed cells regulating their chromatin less tightly18. The computation of the CytoTRACE score c with CellRank 2 is composed of three main steps (Extended Data Fig. 4a). Consider the gene expression matrix X and the smoothed gene expression matrix X(smoothed) found by nearest-neighbor smoothing as implemented in scVelo8 or MAGIC76. For each cell j, we compute the number of genes it expresses (), that is
从概念上讲,CytoTRACE 提出,表达的基因数量会随着细胞成熟度的增加而减少。这一假设的生物学依据是发育程度较低的细胞对其染色质的调控较为宽松 18 。CellRank 2 计算 CytoTRACE 得分 c 主要包括三个步骤(扩展数据图 4a)。考虑基因表达矩阵 X 和通过最近邻平滑得到的平滑基因表达矩阵 X (smoothed) ,该平滑方法如 scVelo 8 或 MAGIC 76 中所实现。对于每个细胞,我们计算其表达的基因数量( ),即
with indicator function . The indicator function equates to one if its argument holds true and zero otherwise. Next, for each gene, we compute its Pearson correlation with GEC, select the top L genes (default 200) and subset X(smoothed) to the identified L genes. Finally, we mean-aggregate each cell’s gene expression
指示函数 。当参数为真时,该指示函数值为 1,否则为 0。接着,针对每个基因,我们计算其与 GEC 的皮尔逊相关系数,选取前 L 个基因(默认 200 个)并将 X (smoothed) 子集限定至这 L 个基因。最后,我们对每个细胞的基因表达进行均值聚合。
with denoting the subsetted, smoothed gene expression matrix X(smoothed). The CytoTRACE score c is then given by scaling to the unit interval
其中 表示经过子集化和平滑处理的基因表达矩阵 X (smoothed) 。随后,通过将 缩放至单位区间,得到 CytoTRACE 得分 c
and the corresponding pseudotime pcyt by inverting c, that is
并通过反演 c 得到对应的伪时间 p cyt ,即
Comparison of the CytoTRACE score construction
CytoTRACE 评分构建方法的比较
Considering the nearest-neighbor-smoothed gene expression matrix, instead of an alternative, computationally more costly imputation scheme, is the main difference between our adaptation and the original CytoTRACE proposal. To impute gene expression, the original implementation solves a non-negative least squares regression problem and simulates a diffusion process18.
我们采用最近邻平滑的基因表达矩阵而非计算成本更高的替代插值方案,这是本方法与原始 CytoTRACE 提案的主要差异。原始实现通过求解非负最小二乘回归问题并模拟扩散过程 18 来完成基因表达插值。
To confirm that our adapted scheme yields numerically similar results, we compared the CytoTRACE scores of the original and our approach to ground truth time or stage labels on six datasets previously used to validate CytoTRACE18 (Extended Data Fig. 4b,c). The considered datasets are bone marrow77 (using 10x and SmartSeq2), C. elegans embryogenesis78 (subsetted to ciliated neurons, hypodermis and seam, or muscle and mesoderm) and zebrafish embryogenesis79. For each dataset, the original CytoTRACE study derived ground truth time labels using either embryo time, stages (C. elegans and zebrafish embryogenesis) or a manual assignment (bone marrow). The concordance of each approach with ground truth was confirmed by calculating the Spearman rank correlation between the CytoTRACE score and ground truth time or stage labels.
为验证我们改进的方案能产生数值相似的结果,我们将原始 CytoTRACE 评分与我们的方法在六个数据集上(这些数据集曾用于验证 CytoTRACE 18 )与真实时间或阶段标签进行了对比(扩展数据图 4b,c)。所用数据集包括骨髓 77 (采用 10x 和 SmartSeq2 技术)、线虫胚胎发育 78 (筛选纤毛神经元、下皮层与接缝细胞或肌肉与中胚层亚群)以及斑马鱼胚胎发育 79 。针对每个数据集,原 CytoTRACE 研究通过胚胎时间、发育阶段(线虫与斑马鱼胚胎)或人工标注(骨髓)获取真实时间标签。通过计算 CytoTRACE 评分与真实时间/阶段标签的斯皮尔曼等级相关系数,证实了两种方法与真实数据的一致性。
The RealTimeKernel: resolving non-equilibria systems through time-series data
RealTimeKernel:通过时间序列数据解析非平衡系统
Commonly used single-cell sequencing protocols are destructive by design and offer, thus, only a discrete temporal resolution. Recent advances allow reconstructing transcriptomic changes across experimental time points using OT15; however, these approaches focus only on inter-time-point information; conversely, the RealTimeKernel incorporates both inter- and intra-time-point transitions to draw a more complete picture of cellular dynamics.
常用的单细胞测序方案在设计上具有破坏性,因此仅能提供离散的时间分辨率。最新进展允许利用 OT 15 重建跨实验时间点的转录组变化;然而,这些方法仅关注时间点间的信息;相反,RealTimeKernel 通过整合时间点间和时间点内的转移信息,能更完整地描绘细胞动态变化。
To quantify inter-time-point transitions, the RealTimeKernel relies on WOT15. For each tuple of consecutive time points tj and tj+1, WOT identifies a transport map , assigning each cell at time tj its likely future state at time tj+1. In addition, we rely on transcriptomic similarity to study transcriptomic change within a single time point tj. We combine WOT-based inter-time point transport maps with similarity-based intra-time-point transition matrices in a global transition matrix T which contains cells from all time points. In the global transition matrix T, we place WOT-computed transport maps on the first off-diagonal, modeling transitions between subsequent time points, and similarity-based transition matrices on the diagonal, modeling transitions within each time point (Fig. 4a). We normalize each row to sum to one, giving rise to a Markov chain description of the system.
为量化时间点间的转移概率,RealTimeKernel 基于 WOT 算法 15 。对于每对连续时间点 t 和 t+1 j+1 ,WOT 会构建一个传输映射 ,将时间点 t 的每个细胞与其在时间点 t+1 的可能未来状态对应 j+1 。此外,我们利用转录组相似性研究单个时间点 t 内的转录组变化。通过将基于 WOT 的时间点间传输映射 与基于相似性的时间点内转移矩阵 整合,我们构建了包含所有时间点细胞的全局转移矩阵 T。在该矩阵中,WOT 计算的传输映射位于第一条非对角线上(模拟相邻时间点间的转移),而基于相似性的转移矩阵位于对角线上(模拟各时间点内的转移)(图 4a)。我们对每行进行归一化处理使其总和为 1,从而建立该系统的马尔可夫链模型。
Thresholding transport maps for scalability
通过阈值化传输映射实现可扩展性
In the single-cell domain, most OT-based approaches, including WOT, rely on entropic regularization36 to speed up the computation of transport maps; however, entropic regularization leads to dense transport maps , rendering downstream computations based on the RealTimeKernel extremely expensive for larger datasets (Extended Data Fig. 6c); most of the entries found in are extremely small, though. As a result, these entries contribute only marginally to the observed dynamics (Extended Data Fig. 6d).
在单细胞领域,大多数基于最优传输(OT)的方法(包括 WOT)依赖熵正则化 36 来加速传输图的计算;然而,熵正则化会导致密集的传输图 ,这使得基于 RealTimeKernel 的下游计算对于较大数据集极为昂贵(扩展数据图 6c);尽管 中的大多数条目极小。因此,这些条目对观测到的动力学贡献微乎其微(扩展数据图 6d)。
To ensure fast RealTimeKernel-based computations, we devised an adaptive thresholding scheme resulting in sparse transition matrices. Transition probabilities falling below a certain threshold are set to zero, all others are kept unchanged. Per default, we identify the smallest threshold τ that does not remove all transitions for any cell, that is
为确保基于 RealTimeKernel 的快速计算,我们设计了一种自适应阈值方案,从而生成稀疏的转移矩阵。低于特定阈值的转移概率被设为零,其余保持不变。默认情况下,我们确定最小阈值τ,该阈值不会移除任何细胞的所有转移,即
with indicator function . Alternatively, the same heuristic can be applied for each time point independently or a user-defined threshold may be used. Following thresholding, we re-normalize the transition matrix such that rows sum to one again.
使用指示函数 。或者,可以对每个时间点独立应用相同的启发式方法,也可以采用用户自定义的阈值。完成阈值处理后,我们重新对转移矩阵进行归一化,使其行和再次为一。
To verify that thresholding the transition matrix does not alter biological findings, we compared fate probabilities derived from the original and the thresholded transition matrix on a dataset of MEF reprogramming15. For each terminal state, we computed the Pearson correlation between fate probabilities estimated by each approach (Extended Data Fig. 6d).
为验证转移矩阵的阈值处理不会改变生物学发现结果,我们在 MEF 重编程数据集 15 上比较了原始转移矩阵与阈值处理后矩阵所得的命运概率。针对每个终末状态,我们计算了两种方法估计的命运概率之间的皮尔逊相关系数(扩展数据图 6d)。
Estimating cellular fate from time-resolved single-cell RNA sequencing data
从时间分辨单细胞 RNA 测序数据估计细胞命运
Traditional single-cell sequencing protocols include cell lysis and are, thus, destructive by nature. Consequently, the transcriptome can only be measured once, resulting in snapshot data. Recently, metabolic-labeling approaches have been extended to single-cell resolution, providing an opportunity to overcome this challenge by measuring newly synthesized mRNA in a given time window80. To label transcripts, current protocols rely on the nucleoside analogs 4-thiouridine (4sU; scSLAM-seq12, sci-fate10, NASC-seq81, scNT-seq11, Well-TEMP-seq82 and others83) or 5-ethynyl-uridine (5EU; scEU-seq9, spinDrop65, TEMPOmap13 and others66).
传统的单细胞测序方案包含细胞裂解步骤,因此本质上是破坏性的。这导致转录组只能测量一次,从而获得的是静态快照数据。最近,代谢标记方法已扩展到单细胞分辨率,通过测量特定时间窗口内新合成的 mRNA,为解决这一挑战提供了可能 80 。目前用于标记转录本的方案主要依赖核苷类似物 4-硫尿苷(4sU;如 scSLAM-seq 12 、sci-fate 10 、NASC-seq 81 、scNT-seq 11 、Well-TEMP-seq 82 等 83 )或 5-乙炔基尿苷(5EU;如 scEU-seq 9 、spinDrop 65 、TEMPOmap 13 等 66 )。
Our study considers two types of labeling experiments: pulse and chase9. Pulse experiments consist of labeling n cell cultures, starting at times tj, j ∈ {1, …, n}. Conversely, in chase experiments, cells are exposed to nucleoside analogs for long enough (for example, more than 24 h), resulting in only labeled transcripts. Following, these labeled transcripts are washed out, starting at times tj. Similar to the pulse experiment, chase experiments include, in general, washing out at n different times. Finally, in both types of experiments, all cells are sequenced at a time tf, naturally defining the labeling time (or duration) by .
本研究考虑两种标记实验类型:脉冲实验与追踪实验 9 。脉冲实验包含对 n 个细胞培养物进行标记,起始时间 t ∈ {1, …, n}。相反,在追踪实验中,细胞会长时间暴露于核苷类似物(例如超过 24 小时),从而仅产生标记转录本。随后,这些标记转录本从不同起始时间 t 开始被清除。与脉冲实验类似,追踪实验通常也包含 n 个不同时间点的清除操作。最终,在这两类实验中,所有细胞均在时间点 t 进行测序,自然将标记时间(或持续时间)定义为 。
Pulse and chase experiments allow measuring the production of mRNA. Here, we estimate cell-specific transcription and degradation rates, similar to a previous proposal in the scEU-seq study9. Specifically, for a particular gene, we assume mRNA levels r to evolve according to
脉冲与追踪实验可用于测量 mRNA 的生成量。我们采用与 scEU-seq 研究 9 类似的方案,估算细胞特异性转录速率和降解速率。具体而言,对于特定基因,我们假设 mRNA 水平 r 的演变遵循
with transcription rate α and degradation rate γ. The corresponding solution is given by
Note that here, we assume gene-specific models, that is, gene–gene interactions are neglected. In the following, we will identify mRNA measurements from pulse and chase experiments by the superscripts (p) and (c), respectively.
Pulse experiments
Pulse experiments study the production of labeled RNA. As labeling starts at tk, and no labeled transcripts exist before, the abundance of labeled mRNA rl at times tk and is given by
and
Chase experiments
In chase experiments, mRNA degradation is studied by washing out labeled transcripts. Thus, labeled mRNA at time follows
where r0 corresponds to the mRNA level when starting to wash out labeled transcripts. Before washing out labeled mRNA, no unlabeled transcripts are present, and thus, their abundance at time is modeled as
Parameter inference
Considering measurements from both chase and pulse experiments, we denote the respective set of cells by and . To estimate cell j and gene g specific model parameters α(j, g), γ(j, g), and , we proceed as follows:
-
1.
Consider cell j and its principal component analysis (PCA) representation . For each labeling duration k, we determine the distance in PCA space between the reference cell j to each cell with labeling duration . For each gene g, we then identify the 20 nearest cells with non-trivial expression in g. These cells, as well as all closer neighbors (with zero counts), define the set , which we consider for parameter inference.
-
2.
To estimate model parameters, we minimize the quadratic loss ℓ defined as
Here, denotes the characteristic function equaling to 1 if , and 0 otherwise. We note that estimating the parameters of a pulse (chase) experiment requires at least two (three) labeling durations.
Our approach differs from the scEU-seq study9 mainly in two ways. First, we base our analysis on total RNA, not spliced RNA. We reasoned that this approach circumvents limitations of identifying unspliced and spliced counts. Second, we infer rates for all genes and not only those changing substantially during development.
Method comparison
To benchmark the performance of different approaches, we identified and ranked potential drivers of every lineage using each approach. We compared this ranking to a curated list of known lineage markers and regulators. If the literature-based gene set were complete, an optimal method would rank the corresponding genes highest. Consequently, for each method, we quantified its performance as follows. First, consider a lineage, a set of known drivers and a method m. Further, denote the set of genes by , and for , identify its assigned rank by a superscript, for example, g(j) for the jth ranked gene g. Next, for each threshold and , we computed how many known markers/regulators were ranked among the top N genes with
Thus, we call an assignment optimal when
Next, for each method m, we computed the area under the curve, AUC(m) of φ(m), that is
and its relative area under the curve, AUCrel(m) as
with
that is, the area under the curve of an optimal assignment.
Datasets
Unless stated otherwise, all functions were run with default parameters. We ran our analyses in Python, relying on the standard single-cell biology tools Scanpy84 and AnnData85; we specify other relevant packages where applicable. For Scanpy-based workflows84, we computed PCA embeddings, neighbor graphs and UMAP embeddings86 with the scanpy.tl.pca, scanpy.pp.neighbors and scanpy.tl.umap functions, respectively.
For analyses based on CellRank 2 kernels, the kernel method compute_transition_matrix computed transition probabilities, and the kernel method cbc the CBC score. We used the GPCCA estimator functions to compute macrostates (compute_macrostates)20 and the TSI score (tsi), define terminal states (set_terminal_states), compute fate probabilities (compute_fate_probabilities) and identify lineage-correlated genes (compute_lineage_drivers). To order the putative regulators according to their peak expression in pseudotime, we first fitted generalized additive models to describe gene expression change over pseudotime with cellrank.models.GAM. Following this, we visualized the putative cascade of regulation with the cellrank.pl.heatmap function.
Human hematopoiesis
All analyses were conducted on the dataset preprocessed by the original study26, subsetted to the normoblast, dendritic and monocyte lineages according to the provided cell type annotation (‘HSC’, ‘MK/E progenitors’, ‘Proerythroblast’, ‘Erythroblast’, ‘Normoblast’, ‘cDC2’, ‘pDC’, ‘G/M prog’ and ‘CD14+ Mono’).
Pseudotime-based analysis
After subsetting the data, we computed the nearest-neighbor graph on the precomputed MultiVI84,87 latent space and the UMAP embedding with Scanpy. Following this, we computed 15 diffusion components88 (scanpy.tl.diffmap) to then assign diffusion pseudotime values using Scanpy’s dpt1,88 function with n_dcs=6. We identified the root cell as the hematopoietic stem cell with the largest fifth diffusion component.
We computed the transition matrix with CellRank 2’s PseudotimeKernel and thresholding_scheme=‘soft’ and computed six macrostates20. We defined the terminal states ‘pDC’, ‘CD14+ Mono’, ‘Normoblast’ and ‘cDC2’ that corresponded to the four macrostates with the largest macrostate purity. After quantifying fate probabilities, we identified putative pDC lineage drivers with our correlation-based procedure, restricted to the hematopoietic stem cell (HSC) and pDC clusters (lineages=[‘pDC’] and clusters=[‘HSC’, ‘pDC’]). We quantified the corresponding gene trends in the same way as described in our previous work14.
RNA velocity-based analysis
基于 RNA 速率分析
To infer RNA velocity, we generally followed the instructions provided by scVelo’s8 tutorials. First, we filtered for genes expressed in at least 20 cells in both unspliced and spliced counts with scVelo’s scvelo.pp.filter_genes function and normalized counts with scvelo.pp.normalize_per_cell. The neighbor graph was again computed on the MultiVI latent space, followed by count imputation through first-order moments with scVelo’s scvelo.pp.moments function. We then inferred RNA velocity with the scvelo.tl.recover_dymanics function.
To quantify cellular fate, we computed transition matrices with the VelocityKernel and ConnectivityKernel and combined them with 0.8 and 0.2 weight, respectively, as proposed by the CellRank 1 workflow. We computed macrostates and fate probabilities using the GPCCA estimator as described for the pseudotime-based analysis. As the RNA-velocity-based analysis did not identify the cDC cluster as a macrostate (Extended Data Fig. 3b,f), we computed three macrostates corresponding to the terminal states normoblasts, monocytes and pDCs.
Embryoid body development
Data preprocessing 数据预处理
We followed Scanpy’s workflow to process the raw count matrix. As a first step, we filtered out genes expressed in fewer than ten cells (scanpy.pp.filter_genes with min_cells=10). Following, we removed cells with more than 17,500 counts, cells for which more than 15% of counts originate from mitochondrial genes and cells expressing more than 3,500 genes. Following, we size normalized cells to 10,000 (scanpy.pp.normalize_total with total_sum=1e4), applied a log1p-transformation (scanpy.pp.log1p) and annotated highly variable genes with scanpy.pp.highly_variable_genes. We based all further analyses on these highly variable genes and the marker genes identified by the study introducing the embryoid body development dataset32. The neighbor graph was computed for 30 neighbors using 30 principal components (PCs).
CytoTRACEKernel analysis
To compute the CytoTRACE score18, we first imputed the normalized count matrix by first-order moments with scVelo’s scvelo.pp.moments function; the score itself was calculated with the compute_cytotrace method of the CytoTRACEKernel. We computed the transition matrix with the soft thresholding scheme (thresholding_scheme=‘soft’) and nu=5. Putative drivers of the endoderm lineage were identified by focusing on the stem cell and endoderm clusters (lineages=[‘EN-1’] and clusters=[‘ESC’]).
Pseudotime construction
To compute DPT1, we calculated diffusion components (scanpy.tl.diffmap) and identified the putative root cell as the minimum in the first diffusion component. We then assigned DPT values using Scanpy’s dpt function.
For the Palantir pseudotime5, we used the corresponding Python package and followed the steps outlined in its documentation. As a first step, we computed the first five diffusion components with palantir.utils.run_diffusion_maps with n_components=5. Following this, we identified the multi-scale space of the data (palantir.utils.determine_multiscale_space) and imputed the data using MAGIC76 (palantir.utils.run_magic_imputation). Finally, we computed the Palantir pseudotime via palantir.core.run_palantir using the same root cell as for our DPT analysis, and num_waypoints=500.
Mouse embryonic fibroblast reprogramming
Data preprocessing 数据预处理
For analyzing the dataset of MEF reprogramming toward induced pluripotent stem cells15, we subsetted to the serum condition and added the category ‘MEF/other’ to the cell set annotations. Then, we computed the PCA embedding and nearest-neighbor graph.
WOT-based analysis 基于 WOT 的分析
To construct transport maps, we used the wot package15 and followed the provided tutorials. First, we instantiated an OT model (wot.ot.OTModel with day_field=‘day’) and computed the transport maps next (compute_all_transport_maps). We defined the target cell sets based on the provided cell type annotation and quantified WOT-based fates toward the last experimental time point through the OT model’s fates function with at_time=18.
为构建转运图谱,我们使用 wot 软件包 15 并遵循提供的教程。首先实例化 OT 模型(wot.ot.OTModel,参数 day_field=‘day’),随后计算转运图谱(compute_all_transport_maps)。基于给定的细胞类型注释定义目标细胞集,并通过 OT 模型的 fates 函数(参数 at_time=18)量化指向最终实验时间点的 WOT 命运。
RealTimeKernel-based analysis
基于 RealTimeKernel 的分析
For our RealTimeKernel-based analysis, we relied on the transport maps computed with wot. When constructing the transition matrix, we considered within-time-point transitions for every experimental time point and weighed them by 0.2 (self_transitions=‘all’, conn_weight=0.2).
在基于 RealTimeKernel 的分析中,我们依赖 wot 计算的转运图谱。构建转移矩阵时,为每个实验时间点考虑时间点内转移,并以 0.2 加权(参数 self_transitions=‘all’,conn_weight=0.2)。
To construct the real-time-informed pseudotime, we symmetrized the global transition matrix and row-normalized it. The symmetrized matrix defined the _transitions_sym attribute of Scanpy’s DPT class. Following, we computed diffusion components with the DPT class’ compute_eigen function. The root cell for DPT was identified as an extremum of the most immature cell state within the first experimental time point in diffusion space. Here, we selected the maximum in the first diffusion component. Finally, we computed DPT itself with scanpy.tl.dpt.
为构建实时信息化的伪时间,我们对全局转移矩阵进行对称化处理并执行行归一化。该对称化矩阵定义了 Scanpy 中 DPT 类的_transitions_sym 属性。随后使用 DPT 类的 compute_eigen 函数计算扩散组分。DPT 的根细胞被确定为扩散空间中第一个实验时间点内最不成熟细胞状态的极值点,此处我们选择第一扩散组分的最大值。最后通过 scanpy.tl.dpt 计算 DPT 本身。
We computed fate probabilities toward the four terminal states according to our canonical pipeline (identification of four macrostates followed by fate quantification).
我们按照标准流程(先识别四种宏观状态,再进行命运定量)计算了向四个终末状态发展的命运概率。
Pseudotime construction 伪时间构建
To assign each observation its DPT1 value, irrespective of experimental time points, we computed diffusion maps (scanpy.tl.diffmap) and identified the root cell as the maximum value in the first diffusion component. Then, we computed DPT with scanpy.tl.dpt.
为给每个观测值分配其 DPT 1 值(不受实验时间点影响),我们计算了扩散映射(scanpy.tl.diffmap)并将根细胞识别为第一扩散组分中的最大值,随后通过 scanpy.tl.dpt 计算 DPT。
For constructing the Palantir pseudotime5, irrespective of experimental time points, we followed the same steps as described for the embryoid body development data.
为构建 Palantir 伪时间轨迹(与实验时间点无关),我们遵循了与胚状体发育数据相同的处理步骤。
Pharyngeal endoderm development
咽内胚层发育
Data preprocessing 数据预处理
The pharyngeal endoderm development dataset provided by the original study37 had already been filtered for high-quality cells and genes. Consequently, we directly quantified highly expressed genes using Scanpy’s highly_variable_genes function. Then, we computed the PCA embedding and nearest-neighbor graph based on 30 PCs and 30 neighbors (n_pcs=30, n_neighbors=30).
原始研究 37 提供的咽内胚层发育数据集已预先过滤了高质量细胞和基因。因此,我们直接使用 Scanpy 的 highly_variable_genes 函数量化高表达基因,随后基于 30 个主成分和 30 个邻近细胞(n_pcs=30, n_neighbors=30)计算了 PCA 嵌入和最近邻图。
RealTimeKernel-based analysis
基于 RealTimeKernel 的分析
To study the pharyngeal endoderm development dataset with the RealTimeKernel, we followed the WOT tutorials to compute transport maps. First, we instantiated an OT model (wot.ot.OTModel with day_field=‘day’) and computed the transport maps next (compute_all_transport_maps). For the RealTimeKernel, we considered within-time-point transitions for every experimental time point and weighed them by 0.1 (self_transitions=‘all’, conn_weight=0.1).
为使用 RealTimeKernel 研究咽内胚层发育数据集,我们遵循 WOT 教程计算传输图谱。首先实例化 OT 模型(wot.ot.OTModel,参数 day_field=‘day’),随后计算传输图谱(compute_all_transport_maps)。对于 RealTimeKernel,我们考虑了每个实验时间点的同时间点转换,并将其权重设为 0.1(self_transitions=‘all’, conn_weight=0.1)。
We estimated terminal states using the GPCCA estimator with default settings by computing 13 macrostates and selecting the known terminal clusters. After calculating fate probabilities, for each lineage, we identified lineage-correlated genes as candidate driver genes with GPCCA.compute_lineage_drivers by restricting the analysis to progenitors of the corresponding lineage and excluding cell cycle, mitochondrial, ribosomal and hemoglobin genes89.
我们使用默认设置的 GPCCA 估计器,通过计算 13 个宏观状态并选择已知的终末簇来估计终末状态。在计算命运概率后,针对每个谱系,我们通过将分析限制于相应谱系的祖细胞并排除细胞周期、线粒体、核糖体和血红蛋白基因,利用 GPCCA.compute_lineage_drivers 方法鉴定出谱系相关基因作为候选驱动基因 89 。
To study mTEC development, we subsetted to the early thymus, ultimobranchial body (UBB), parathyroid, cTEC and mTEC clusters and processed the data as described for the entire dataset. We computed the UMAP embedding using Scanpy’s umap function. To compute the transition matrix, we proceeded in the same manner as described for the entire dataset. For TSI, fate quantification, and driver analysis, we followed the standard CellRank 2 pipeline.
为了研究 mTEC 的发育过程,我们选取了早期胸腺、后鳃体(UBB)、甲状旁腺、cTEC 和 mTEC 细胞群作为子集,并按照全数据集的处理流程对这些数据进行了分析。我们使用 Scanpy 的 umap 函数计算了 UMAP 降维嵌入。在计算转移矩阵时,采用了与全数据集相同的处理方法。对于 TSI 分析、命运量化及驱动因子分析,我们遵循了 CellRank 2 的标准流程。
WOT-based analysis
To identify putative drivers of the mTEC lineage with WOT, we used the same transport maps as in our RealTimeKernel-based analysis. We defined the target cell sets based on the provided cell type annotation considering only observations from the last time point and computed the pullback distribution from the mTEC cluster at embryonic day (E) 12.5 to E10.5 cells as it consists of progenitor cells (pull_back). The sequence of ancestor distributions was quantified with the transport model’s trajectories method. WOT identifies putative drivers of the mTEC lineage as genes differentially expressed in cells most fated toward the mTEC cluster. We used the wot.tmap.diff_exp function to construct the corresponding gene ranking.
Classical differential expression analysis
As an alternative means to identify putative drivers of the mTEC lineage based on the fate probabilities assigned by our RealTimeKernel-based analysis, we defined two groups of cells within the general progenitor pool, those with mTEC fate probability greater than 0.5 and all other progenitor cells. We then identified differentially expressed genes between putative mTEC progenitors and all others with Scanpy’s rank_genes_groups function.
Intestinal organoids 肠道类器官
Data preprocessing 数据预处理
To preprocess the dataset of intestinal organoids, we first excluded dimethylsulfoxide control cells and cells labeled as tuft cells. Following, we removed genes with fewer than 50 counts, size normalized total and labeled counts, and identified the 2,000 most highly variable genes with scvelo.pp.filter_and_normalize. The neighbor graph was constructed based on 30 PCs and 30 neighbors. Finally, we computed first-order-smoothed labeled and total mRNA counts.
为预处理肠道类器官数据集,我们首先排除了二甲基亚砜对照组细胞和被标记为簇细胞的细胞。随后,我们剔除了计数少于 50 的基因,对总计数和标记计数进行了大小标准化,并使用 scvelo.pp.filter_and_normalize 筛选出 2000 个高变基因。基于 30 个主成分和 30 个邻近点构建了邻域图。最后,我们计算了一阶平滑处理的标记 mRNA 计数和总 mRNA 计数。
Parameter estimation 参数估计
To estimate kinetic rate parameters, we made use of our new inference scheme for metabolic-labeling data implemented as part of the scVelo package. We first masked observations according to their labeling time with scvelo.inference.get_labeling_time_mask. Next, we computed pairwise distances between observations in PCA space and sorted observations in ascending order for each time point using scvelo.inference.get_obs_dist_argsort. This information allowed us to identify, for each cell and gene, how many neighbors to consider during parameter estimation to include 20 non-zero observations smoothed by first-order moments. This calculation was performed via scvelo.inference.get_n_neighbors. Finally, we estimated model parameters based on smoothed labeled counts with scvelo.inference.get_parameters.
为估算动力学速率参数,我们采用了 scVelo 软件包中实现的新推断方案处理代谢标记数据。首先利用 scvelo.inference.get_labeling_time_mask 根据标记时间对观测值进行掩膜处理。随后在 PCA 空间中计算观测值的成对距离,并通过 scvelo.inference.get_obs_dist_argsort 对各时间点的观测值进行升序排序。这些信息使我们能够确定每个细胞和基因在参数估计时应考虑的邻居数量,以确保包含 20 个经一阶矩平滑的非零观测值,该计算通过 scvelo.inference.get_n_neighbors 完成。最后,我们基于平滑后的标记计数数据,使用 scvelo.inference.get_parameters 进行模型参数估计。
Labeling velocity-based analysis
基于速度分析的标记
To quantify cell-specific fates, we first computed labeled velocities based on the estimated parameters. Then, we computed a transition matrix by combining the VelocityKernel and ConnectivityKernel with a 0.8 and 0.2 weight, respectively. We then inferred 12 macrostates and fate probabilities toward the known terminal states. Lineage-specific drivers were identified by restricting the correlation-based analysis to the corresponding terminal state and stem cell cluster. For putative driver gene ranking based on gene expression, we correlated fate probabilities with smoothed labeled counts.
为量化细胞特异性命运,我们首先基于估计参数计算标记速度。随后通过将 VelocityKernel 与 ConnectivityKernel 以 0.8 和 0.2 的权重组合计算转移矩阵。接着我们推断出 12 个宏观状态及朝向已知终末状态的命运概率。通过将基于相关性的分析限定于对应终末状态和干细胞簇,识别出谱系特异性驱动基因。基于基因表达的假定驱动基因排序,是通过将命运概率与平滑标记计数进行相关性分析实现的。
Dynamo-based analysis 基于 Dynamo 的分析
To analyze the intestinal organoid data with dynamo16, we followed the tutorials provided in the documentation of the Python package. As a first step, this required us to compute the ratio of new to total RNA with dynamo.preprocessing.utils.calc_new_to_total_ratio followed by first-order moment imputation of total and new RNA using dynamo.tl.moments with our connectivity matrix and group=‘time’. Dynamo’s dynamo.tl.dynamics estimated the velocities with function arguments model=‘deterministic’, tkey=‘time’ and assumption_mRNA=‘ss’.
为使用 dynamo 16 分析肠道类器官数据,我们遵循了该 Python 包文档中的教程流程。第一步需要使用 dynamo.preprocessing.utils.calc_new_to_total_ratio 计算新 RNA 与总 RNA 的比值,随后通过 dynamo.tl.moments 对总 RNA 和新 RNA 进行一阶矩插补(使用连接矩阵及 group='time'参数)。Dynamo 的 dynamo.tl.dynamics 函数以 model='deterministic'、tkey='time'和 assumption_mRNA='ss'参数估计了 RNA 速度。
Following velocity estimation, we quantified fixed points by following dynamo’s corresponding pipeline. First, we projected the high-dimensional velocity field of new RNA onto the UMAP embedding using dynamo.tl.cell_velocities with ekey=‘M_n’ and vkey=‘velocity_N’. Fixed points were then identified by calling dynamo.tl.VectorField with basis=‘umap’ and dynamo.vf.topography. As a final step, we identified all stable fixed points.
在完成速度估计后,我们通过遵循 dynamo 的对应流程量化了固定点。首先,使用 dynamo.tl.cell_velocities(参数 ekey='M_n',vkey='velocity_N')将新 RNA 的高维速度场投影至 UMAP 嵌入空间。随后通过调用 dynamo.tl.VectorField(参数 basis='umap')结合 dynamo.vf.topography 识别固定点。最后一步,我们确定了所有稳定固定点。
Given the stable fixed points of the system, we identified lineage-correlated genes regulating cell differentiation toward them using dynamo’s least action path analysis. As a first step, this workflow required us to compute a UMAP embedding based on new RNA with dynamo.tl.reduceDimension and layer=‘X_new’, followed by the projection of the velocity field onto the PCA space (dynamo.tl.cell_velocities with basis=‘pca’) and learning a vector field function based on this projection (dynamo.tl.VectorField with basis=‘pca’). Next, we defined terminal states as the 30 nearest neighbors in UMAP space of each stable fixed point. For initial states, we computed the 30 nearest neighbors of unstable fixed points of the stem cell cluster. To compute the least action paths and account for uncertainty in initial and terminal state assignment, we randomly sampled ten pairs of initial and terminal cells and estimated the paths between them with dynamo.pd.least_action. Dynamo’s dynamo.pd.GeneTrajectory class then identified genes associated with the emergence of a terminal state. The pairwise sampling of initial and terminal cells defined the confidence bands of dynamo’s gene rankings shown in Fig. 5d.
在确定了系统的稳定不动点后,我们利用 dynamo 的最小作用路径分析技术,识别出调控细胞向这些不动点分化的谱系相关基因。该工作流程首先要求我们基于新 RNA 数据(使用 dynamo.tl.reduceDimension,layer='X_new')计算 UMAP 降维嵌入,随后将速度场投影到 PCA 空间(通过 dynamo.tl.cell_velocities,basis='pca'),并基于此投影学习向量场函数(使用 dynamo.tl.VectorField,basis='pca')。接着,我们将终末状态定义为每个稳定不动点在 UMAP 空间中的 30 个最近邻。对于初始状态,我们计算了干细胞簇不稳定不动点的 30 个最近邻。为计算最小作用路径并考虑初始与终末状态分配的不确定性,我们随机抽取了十对初始与终末细胞,通过 dynamo.pd.least_action 估算其间的路径。随后,dynamo 的 dynamo.pd.GeneTrajectory 类识别出与终末状态形成相关的基因。初始与终末细胞的配对抽样过程界定了图中所展示的 dynamo 基因排序置信带。 5d.
RNA velocity-based analysis
基于 RNA 速率分析
Conventional RNA velocity was estimated with scVelo’s dynamical model8 by running scvelo.tl.recover_dynamics. To execute this function, we first preprocessed the raw data with scvelo.pp.filter_and_normalize to remove genes expressed in fewer than 50 cells (min_counts=50), size-normalizing spliced and unspliced counts and subsetting to the 2,000 most highly variable genes (n_top_genes=2000). Then, we computed the PCA embedding, calculated the neighbor graph with 30 PCs and 30 neighbors and smoothed unspliced and spliced counts by first-order moments (scvelo.pp.moments).
使用 scVelo 的动态模型 8 通过运行 scvelo.tl.recover_dynamics 估算常规 RNA 速率。执行此函数前,我们先用 scvelo.pp.filter_and_normalize 预处理原始数据:剔除在少于 50 个细胞中表达的基因(min_counts=50),对剪接和未剪接计数进行大小标准化,并筛选出 2000 个高变基因(n_top_genes=2000)。接着计算 PCA 嵌入,用 30 个主成分和 30 个邻居构建邻域图,并通过一阶矩平滑未剪接和剪接计数(scvelo.pp.moments)。
We combined the VelocityKernel and ConnectivityKernel weighted by 0.8 and 0.2, respectively, to estimate the cell–cell transition matrix. Next, we identified terminal states and corresponding fates and lineage-correlated gene rankings following the canonical CellRank 2 pipeline.
我们将 VelocityKernel 和 ConnectivityKernel 按 0.8 和 0.2 的权重组合,估算细胞间转移矩阵。随后遵循标准 CellRank 2 流程识别终末状态、对应命运及谱系相关基因排序。
Reporting summary 报告摘要
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
研究设计的更多信息详见本文关联的《自然》系列期刊报告摘要。
Data availability 数据可用性
All data presented in this study are publicly available via the original publications; we provide additional access to each dataset, that is, the peripheral blood mononuclear cell, embryoid body development, MEF, pharyngeal endoderm development and intestinal organoid data, via a figshare collection at https://doi.org/10.6084/m9.figshare.c.6843633.v1 (ref. 90).
本研究中展示的所有数据均通过原始出版物公开获取;我们还通过 figshare 合集(https://doi.org/10.6084/m9.figshare.c.6843633.v1,参考文献 90 )提供了对每个数据集的额外访问途径,包括外周血单个核细胞、胚状体发育、MEF、咽内胚层发育和肠道类器官数据。
Code availability 代码可用性
CellRank 2 is released under the BSD-3-Clause license, with code available at https://github.com/theislab/cellrank and deposited via Zenodo at https://zenodo.org/doi/10.5281/zenodo.10210196 (ref. 91). The inference of kinetic rates based on metabolic-labeling data is implemented as part of the scVelo package (https://github.com/theislab/scvelo). Code to reproduce the results in the paper can be found at https://github.com/theislab/cellrank2_reproducibility and deposited via Zenodo at https://doi.org/10.5281/zenodo.10809425 (ref. 92).
CellRank 2 以 BSD-3-Clause 许可证发布,代码可在 https://github.com/theislab/cellrank 获取,并通过 Zenodo 存档于 https://zenodo.org/doi/10.5281/zenodo.10210196(参考文献 91 )。基于代谢标记数据的动力学速率推断功能已集成至 scVelo 软件包(https://github.com/theislab/scvelo)。重现论文结果的代码存放于 https://github.com/theislab/cellrank2_reproducibility,并通过 Zenodo 存档于 https://doi.org/10.5281/zenodo.10809425(参考文献 92 )。
References 参考文献
Haghverdi, L., Büttner, M., Wolf, F. A., Buettner, F. & Theis, F. J. Diffusion pseudotime robustly reconstructs lineage branching. Nat. Methods 13, 845–848 (2016).
Qiu, X. et al. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods 14, 979–982 (2017).
Street, K. et al. Slingshot: cell lineage and pseudotime inference for single-cell transcriptomics. BMC Genomics 19, 477 (2018).
Wolf, F. A. et al. PAGA: graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. Genome Biol. 20, 59 (2019).
Wolf, F. A. 等. PAGA:通过保留单细胞拓扑结构的图抽象方法协调聚类分析与轨迹推断. Genome Biol. 20, 59 (2019).Setty, M. et al. Characterization of cell fate probabilities in single-cell data with Palantir. Nat. Biotechnol. 37, 451–460 (2019).
Setty, M. 等. 使用 Palantir 对单细胞数据中的细胞命运概率进行表征. 自然-生物技术 37, 451–460 (2019).Nowotschin, S. et al. The emergent landscape of the mouse gut endoderm at single-cell resolution. Nature 569, 361–367 (2019).
Nowotschin, S. 等. 单细胞分辨率下小鼠肠道内胚层的新兴景观. 自然 569, 361–367 (2019).La Manno, G. et al. RNA velocity of single cells. Nature 560, 494–498 (2018).
拉·曼诺等. 单细胞 RNA 速率分析. 《自然》560 卷, 494–498 页 (2018 年).Bergen, V., Lange, M., Peidli, S., Wolf, F. A. & Theis, F. J. Generalizing RNA velocity to transient cell states through dynamical modeling. Nat. Biotechnol. 38, 1408–1414 (2020).
伯根等. 通过动力学建模将 RNA 速率推广至瞬态细胞状态. 《自然·生物技术》38 卷, 1408–1414 页 (2020 年).Battich, N. et al. Sequencing metabolically labeled transcripts in single cells reveals mRNA turnover strategies. Science 367, 1151–1156 (2020).
巴蒂奇等. 单细胞代谢标记转录本测序揭示 mRNA 周转策略. 《科学》367 卷, 1151–1156 页 (2020 年).Cao, J., Zhou, W., Steemers, F., Trapnell, C. & Shendure, J. Sci-fate characterizes the dynamics of gene expression in single cells. Nat. Biotechnol. 38, 980–988 (2020).
Cao, J., Zhou, W., Steemers, F., Trapnell, C. & Shendure, J. Sci-fate 揭示了单细胞中基因表达的动态特征。Nat. Biotechnol. 38, 980–988 (2020).Qiu, Q. et al. Massively parallel and time-resolved RNA sequencing in single cells with scNT-seq. Nat. Meth. 17, 991–1001 (2020).
邱琦等. 单细胞水平大规模并行时间分辨 RNA 测序技术 scNT-seq. 《自然·方法》17 卷, 991–1001 页 (2020 年).Erhard, F. et al. scslam-seq reveals core features of transcription dynamics in single cells. Nature 571, 419–423 (2019).
埃尔哈德等. scslam-seq 揭示单细胞转录动态的核心特征. 《自然》571 卷, 419–423 页 (2019 年).Ren, J. et al. Spatiotemporally resolved transcriptomics reveals the subcellular RNA kinetic landscape. Nat. Meth. 20, 695–705 (2023).
任杰等. 时空分辨转录组学揭示亚细胞 RNA 动力学图谱. 自然·方法 20, 695–705 (2023).Lange, M. et al. Cellrank for directed single-cell fate mapping. Nat. Meth. 19, 159–170 (2022).
Lange, M. 等。CellRank 用于定向单细胞命运图谱绘制。《自然·方法》19 卷, 159–170 页 (2022 年).Schiebinger, G. et al. Optimal-transport analysis of single-cell gene expression identifies developmental trajectories in reprogramming. Cell 176, 928–943 (2019).
Schiebinger, G. 等。单细胞基因表达的最优输运分析识别重编程中的发育轨迹。《细胞》176 卷, 928–943 页 (2019 年).Qiu, X. et al. Mapping transcriptomic vector fields of single cells. Cell 185, 690–711 (2022).
邱, X. 等。单细胞转录组矢量场的映射。《细胞》185 卷, 690–711 页 (2022 年)。Barile, M. et al. Coordinated changes in gene expression kinetics underlie both mouse and human erythroid maturation. Genome Biol. 22, 197 (2021).
Barile, M. 等。基因表达动力学的协同变化是小鼠和人类红细胞成熟的共同基础。《基因组生物学》22, 197 (2021)。Gulati, G. S. et al. Single-cell transcriptional diversity is a hallmark of developmental potential. Science 367, 405–411 (2020).
Gulati, G. S. 等。单细胞转录多样性是发育潜能的标志。《科学》367, 405–411 (2020)。Reuter, B., Weber, M., Fackeldey, K., Röblitz, S. & Garcia, M. E. Generalized Markov state modeling method for nonequilibrium biomolecular dynamics: exemplified on amyloid β conformational dynamics driven by an oscillating electric field. J. Chem. Theory Comput. 14, 3579–3594 (2018).
Reuter, B., Weber, M., Fackeldey, K., Röblitz, S. & Garcia, M. E. 广义马尔可夫状态建模方法在非平衡生物分子动力学中的应用:以振荡电场驱动的淀粉样β构象动力学为例。J. Chem. Theory Comput. 14, 3579–3594 (2018).Reuter, B., Fackeldey, K. & Weber, M. Generalized Markov modeling of nonreversible molecular kinetics. J. Chem. Phys. 150, 174103 (2019).
Reuter, B., Fackeldey, K. 和 Weber, M. 非可逆分子动力学的广义马尔可夫建模。《化学物理杂志》150, 174103 (2019).Forrow, A. & Schiebinger, G. LineageOT is a unified framework for lineage tracing and trajectory inference. Nat. Commun. 12, 4940 (2021).
Forrow, A. 和 Schiebinger, G. LineageOT:谱系追踪与轨迹推断的统一框架。《自然·通讯》12, 4940 (2021).Wang, S.-W., Herriges, M. J., Hurley, K., Kotton, D. N. & Klein, A. M. Cospar identifies early cell fate biases from single-cell transcriptomic and lineage information. Nat. Biotechnol. 40, 1066–1074 (2022).
Wang, S.-W., Herriges, M. J., Hurley, K., Kotton, D. N. 和 Klein, A. M. Cospar 通过单细胞转录组与谱系信息识别早期细胞命运偏向。《自然·生物技术》40, 1066–1074 (2022).Lange, M. et al. Mapping lineage-traced cells across time points with moslin. Preprint at bioRxiv https://doi.org/10.1101/2023.04.14.536867 (2023).
Klein, D. et al. Mapping cells through time and space with moscot. Preprint at bioRxiv https://doi.org/10.1101/2023.05.11.540374 (2023).
Stassen, S. V., Yip, G. G. K., Wong, K. K. Y., Ho, J. W. K. & Tsia, K. K. Generalized and scalable trajectory inference in single-cell omics data with via. Nat.Commun. https://doi.org/10.1038/s41467-021-25773-3 (2021).
Lance, C. et al. in (eds Kiela, D., Ciccone, M. & Caputo, B.) Proc. NeurIPS 2021 Competitions and Demonstrations Track, Vol. 176 Proc. Machine Learning Research 162–176 (PMLR, 2022).
Sawai, C. M. et al. Transcription factor runx2 controls the development and migration of plasmacytoid dendritic cells. J. Exp. Med. 210, 2151–2159 (2013).
Ceribelli, M. et al. A druggable tcf4- and brd4-dependent transcriptional network sustains malignancy in blastic plasmacytoid dendritic cell neoplasm. Cancer Cell 30, 764–778 (2016).
Gao, M., Qiao, C. & Huang, Y. UniTVelo: temporally unified RNA velocity reinforces single-cell trajectory inference. Nat. Commun. 13, 6586 (2022).
Saelens, W., Cannoodt, R., Todorov, H. & Saeys, Y. A comparison of single-cell trajectory inference methods. Nat. Biotechnol. 37, 547–554 (2019).
Cao, J. et al. The single-cell transcriptional landscape of mammalian organogenesis. Nature 566, 496–502 (2019).
Moon, K. R. et al. Visualizing structure and transitions in high-dimensional biological data. Nat. Biotechnol. 37, 1482–1492 (2019).
Chen, Y.-F. et al. Control of matrix stiffness promotes endodermal lineage specification by regulating SMAD2/3 via lncRNA LINC00458. Sci. Adv. https://doi.org/10.1126/sciadv.aay0264 (2020).
Takenaga, M., Fukumoto, M. & Hori, Y. Regulated nodal signaling promotes differentiation of the definitive endoderm and mesoderm from ES cells. J. Cell Sci. 120, 2078–2090 (2007).
Fischer, D. S. et al. Inferring population dynamics from single-cell RNA-sequencing time series data. Nat. Biotechnol. 37, 461–468 (2019).
Cuturi, M. Sinkhorn distances: lightspeed computation of optimal transportation distances. Preprint at arXiv https://doi.org/10.48550/arXiv.1306.0895 (2013).
Magaletta, M. E. et al. Integration of single-cell transcriptomes and chromatin landscapes reveals regulatory programs driving pharyngeal organ development. Nat. Commun. 13, 457 (2022).
Choe, C. P. & Crump, J. G. Dynamic epithelia of the developing vertebrate face. Curr. Opin. Genet. Dev. 32, 66–72 (2015).
Grevellec, A. & Tucker, A. S. The pharyngeal pouches and clefts: development, evolution, structure and derivatives. Semin. Cell Dev. Biol. 21, 325–332 (2010).
Fagman, H., Andersson, L. & Nilsson, M. The developing mouse thyroid: embryonic vessel contacts and parenchymal growth pattern during specification, budding, migration, and lobulation. Dev. Dyn. 235, 444–455 (2005).
Liu, Z., Yu, S. & Manley, N. R. Gcm2 is required for the differentiation and survival of parathyroid precursor cells in the parathyroid/thymus primordia. Dev. Biol. 305, 333–346 (2007).
Posabella, A. et al. Derivation of thyroid follicular cells from pluripotent stem cells: insights from development and implications for regenerative medicine. Front. Endocrinol. https://doi.org/10.3389/fendo.2021.666565 (2021).
Ohigashi, I. et al. Aire-expressing thymic medullary epithelial cells originate from β5t-expressing progenitor cells. Proc. Natl Acad. Sci. USA 110, 9885–9890 (2013).
Rodrigues, P. M. et al. Thymic epithelial cells require p53 to support their long-term function in thymopoiesis in mice. Blood 130, 478–488 (2017).
Bautista, J. L. et al. Single-cell transcriptional profiling of human thymic stroma uncovers novel cellular heterogeneity in the thymic medulla. Nat. Commun. 12, 1096 (2021).
Dooley, J., Erickson, M. & Farr, A. G. Alterations of the medullary epithelial compartment in the aire-deficient thymus: Implications for programs of thymic epithelial differentiation. J. Immunol. 181, 5225–5232 (2008).
Stefanski, H. E. et al. P63 targeted deletion under the foxn1 promoter disrupts pre-and post-natal thymus development, function and maintenance as well as induces severe hair loss. PLoS ONE 17, e0261770 (2022).
Lucas, B. et al. Embryonic keratin19+ progenitors generate multiple functionally distinct progeny to maintain epithelial diversity in the adult thymus medulla. Nat. Commun. 14, 2066 (2023).
Haunerdinger, V. et al. Novel combination of surface markers for the reliable and comprehensive identification of human thymic epithelial cells by flow cytometry: quantitation and transcriptional characterization of thymic stroma in a pediatric cohort. Front. Immunol. https://doi.org/10.3389/fimmu.2021.740047 (2021).
Carter, J. A. et al. Transcriptomic diversity in human medullary thymic epithelial cells. Nat. Commun. 13, 4296 (2022).
Gotter, J., Brors, B., Hergenhahn, M. & Kyewski, B. Medullary epithelial cells of the human thymus express a highly diverse selection of tissue-specific genes colocalized in chromosomal clusters. J. Exp. Med. 199, 155–166 (2004).
Skogberg, G. et al. Human thymic epithelial primary cells produce exosomes carrying tissue-restricted antigens. Immunol. Cell Biol. 93, 727–734 (2015).
Nusser, A. et al. Developmental dynamics of two bipotent thymic epithelial progenitor types. Nature 606, 165–171 (2022).
Haber, A. L. et al. A single-cell survey of the small intestinal epithelium. Nature 551, 333–339 (2017).
Alemany, A., Florescu, M., Baron, C. S., Peterson-Maduro, J. & van Oudenaarden, A. Whole-organism clone tracing using single-cell sequencing. Nature 556, 108–112 (2018).
Raj, B. et al. Simultaneous single-cell profiling of lineages and cell types in the vertebrate brain. Nat. Biotechnol. 36, 442–450 (2018).
Spanjaard, B. et al. Simultaneous lineage tracing and cell-type identification using crispr–cas9-induced genetic scars. Nat. Biotechnol. 36, 469–473 (2018).
Chan, M. M. et al. Molecular recording of mammalian embryogenesis. Nature 570, 77–82 (2019).
Chen, A. et al. Spatiotemporal transcriptomic atlas of mouse organogenesis using DNA nanoball-patterned arrays. Cell 185, 1777–1792 (2022).
Liu, C. et al. Spatiotemporal mapping of gene expression landscapes and developmental trajectories during zebrafish embryogenesis. Dev. Cell 57, 1284–1298 (2022).
Wang, M. et al. High-resolution 3D spatiotemporal transcriptomic maps of developing Drosophila embryos and larvae. Dev. Cell 57, 1271–1283 (2022).
Otto, D., Jordan, C., Dury, B., Dien, C. & Setty, M. Quantifying cell-state densities in single-cell phenotypic landscapes using mellon. Preprint at bioRxiv https://doi.org/10.1101/2023.07.09.548272 (2023).
Maizels, R. J., Snell, D. M. & Briscoe, J. Deep dynamical modelling of developmental trajectories with temporal transcriptomics. Preprint at bioRxiv https://doi.org/10.1101/2023.07.06.547989 (2023).
Peng, Q., Qiu, X. & Li, T. Storm: Incorporating transient stochastic dynamics to infer the rna velocity with metabolic labeling information. Preprint at bioRxiv https://doi.org/10.1101/2023.06.21.545990 (2023).
De Jonghe, J. et al. spinDrop: a droplet microfluidic platform to maximise single-cell sequencing information content. Nat. Commun. 14, 4788 (2023).
Van’t Sant, L. J., White, J. J., Hoeijmakers, J. H. J., Vermeij, W. P. & Jaarsma, D. In vivo 5-ethynyluridine (EU) labelling detects reduced transcription in purkinje cell degeneration mouse mutants, but can itself induce neurodegeneration. Acta Neuropathol Commun. https://doi.org/10.1186/s40478-021-01200-y (2021).
Bergen, V., Soldatov, R. A., Kharchenko, P. V. & Theis, F. J. RNA velocity–current challenges and future perspectives. Mol. Sys. Biol. https://doi.org/10.15252/msb.202110282 (2021).
Weiler, P., Van den Berge, K., Street, K. & Tiberi, S. A Guide to Trajectory Inference and RNA Velocity, 269–292 (Springer, 2022).
Meier, A. B. et al. Epicardioid single-cell genomics uncovers principles of human epicardium biology in heart development and disease. Nat. Biotechnol. 41, 1787–1800 (2023).
Xiao, Y. et al. Tracking single-cell evolution using clock-like chromatin accessibility loci. Nat. Biotechnol. https://doi.org/10.1038/s41587-024-02241-z (2024).
Schölkopf, B. Causality for Machine Learning, 765–804 (ACM, 2022).
Gorin, G., Fang, M., Chari, T. & Pachter, L. RNA velocity unraveled. PLOS Comput. Biol. 18, e1010492 (2022).
Zheng, S. C., Stein-O’Brien, G., Boukas, L., Goff, L. A. & Hansen, K. D. Pumping the brakes on RNA velocity by understanding and interpreting RNA velocity estimates. Genome Biol. 24, 246 (2023).
Jaitin, D. A. et al. Massively parallel single-cell RNA-seq for marker-free decomposition of tissues into cell types. Science 343, 776–779 (2014).
Saad, Y. & Schultz, M. H. Gmres: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869 (1986).
van Dijk, D. et al. Recovering gene interactions from single-cell data using data diffusion. Cell 174, 716–729 (2018).
The Tabla Muris Consortium et al. Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature 562, 367–372 (2018).
Packer, J. S. et al. A lineage-resolved molecular atlas of C. elegans embryogenesis at single-cell resolution. Science https://doi.org/10.1126/science.aax1971 (2019).
Farrell, J. A. et al. Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science https://doi.org/10.1126/science.aar3131 (2018).
Erhard, F. et al. Time-resolved single-cell RNA-seq using metabolic RNA labelling. Nat. Rev. Methods Primers https://doi.org/10.1038/s43586-022-00157-z (2022).
Hendriks, G.-J. et al. NASC-seq monitors RNA synthesis in single cells. Nat. Commun. 10, 3138 (2019).
Lin, S. et al. Well-TEMP-seq as a microwell-based strategy for massively parallel profiling of single-cell temporal RNA dynamics. Nat. Commun. 14, 1272 (2023).
Holler, K. et al. Spatio-temporal mRNA tracking in the early zebrafish embryo. Nat. Commun. 12, 3358 (2021).
Wolf, F. A., Angerer, P. & Theis, F. J. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol. 19, 15 (2018).
Virshup, I., Rybakov, S., Theis, F. J., Angerer, P. & Wolf, F. A. anndata: annotated data. Preprint at bioRxiv https://doi.org/10.1101/2021.12.16.473007 (2021).
McInnes, L., Healy, J., Saul, N. & Großberger, L. UMAP: uniform manifold approximation and projection. J. Open Source Softw. 3, 861 (2018).
Ashuach, T. et al. MultiVI: deep generative model for the integration of multimodal data. Nat. Meth. 20, 1222–1231 (2023).
Haghverdi, L., Buettner, F. & Theis, F. J. Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics 31, 2989–2998 (2015).
Heumos, L. et al. Best practices for single-cell analysis across modalities. Nat. Rev. Genet. 24, 550–572 (2023).
Weiler, P. et al. Unified fate mapping in multiview single-cell data. figshare https://doi.org/10.6084/m9.figshare.c.6843633.v1 (2023).
Klein, M., Weiler, P. & Lange, M. theislab/cellrank: v.2.0.3. Zenodo https://doi.org/10.5281/zenodo.10210197 (2023).
Weiler, P. theislab/cellrank2_reproducibility: v.1.0.0. Zenodo https://doi.org/10.5281/zenodo.10827945 (2024).
Li, S. et al. A relay velocity model infers cell-dependent RNA velocity. Nat. Biotechnol. 42, 99–108 (2023).
Biddy, B. A. et al. Single-cell mapping of lineage and identity in direct reprogramming. Nature 564, 219–224 (2018).
Acknowledgements
We thank N. Battich for helpful discussions about scEU-seq data, R. Maehr and M. Lobo for insights into pharyngeal organ development and T. Nawy for helping to write the paper. We also thank I. Virshup and numerous researchers who provided feedback on our implementation on GitHub. Finally, we thank all members of the Theis and Treutlein laboratories for helpful discussions. This work was supported by the BMBF-funded de.NBI Cloud within the German Network for Bioinformatics Infrastructure (de.NBI) (031A532B, 031A533A, 031A533B, 031A534A, 031A535A, 031A537A, 031A537B, 031A537C, 031A537D and 031A538A) and co-funded by the European Union (ERC, DeepCell, 101054957). M.L. acknowledges financial support from the Joachim Herz Foundation and through an EMBO Postdoctoral Fellowship. F.T. acknowledges support by Wellcome Leap as part of the ΔTissue Program. For all support via EU funding, the views and opinions expressed are those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
Funding
Open access funding provided by Helmholtz Zentrum München - Deutsches Forschungszentrum für Gesundheit und Umwelt (GmbH).
Ethics declarations
Competing interests
F.T. consults for Immunai, Singularity Bio, CytoReason, Cellarity and Curie Bio Operations and has ownership interest in Dermagnostix and Cellarity. D.P. is on the scientific advisory board of Insitro. The other authors declare no competing interests.
Peer review
Peer review information
Nature Methods thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Lin Tang, in collaboration with the Nature Methods team. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Guiding kernel choice in CellRank 2.
CellRank 2 implements various kernels suitable for different data modalities and experimental designs. The diagram may be used as a guide to identify the most suitable kernel. Note that assumptions change as methods evolve; for example, more recent inference schemes for RNA velocity account for non-constant kinetic rates93.
Extended Data Fig. 2 CellRank 2 scales to large cell numbers.
a. Runtime (left) and peak memory consumption (right) to compute fate probabilities with CellRank (orange) and CellRank 2 (blue). Both methods were run on subsets of a reprogramming dataset containing over 100, 000 cells94. Box plots indicate the median (center line), interquartile range (hinges), and whiskers at 1.5x interquartile range (N = 10 runs each). b. The CellRank 2 adaptation of CytoTRACE scales to a mouse organogenesis atlas of 1.3 million cells31, whereas CytoTRACE fails above 80, 000 cells. Box plots indicate the median (center line), interquartile range (hinges), and 1.5x interquartile range (whiskers) (50, 000 cells, original: N = 6 runs; 60, 000 cells, original: N = 8 runs; 80, 000 cells, original: N = 9 runs; otherwise: N = 10 runs). c. Runtime for calculating macrostates and fate probabilities using the RealTimeKernel with (brown) and without (green) thresholded transition matrix. Box plots indicate the median (center line), interquartile range (hinges), and 1.5x interquartile range (whiskers) (N = 10 runs each).
Extended Data Fig. 3 Performance of the VelocityKernel compared to the PseudotimeKernel.
a. UMAP embedding of entire hematopoiesis dataset26. Cell types are colored according to the original publication (HSC: hematopoietic stem cell, MK/E prog: megakaryocyte/erythrocyte progenitors, G/M progenitor: Granulocyte/Myeloid progenitor, pDC: plasmacytoid dendritic cell, cDC2: classical dendritic cells). b. Terminal states identified by the PseudotimeKernel (left) and VelocityKernel with RNA velocity (right) inferred using scVelo’s dynamical model8. c. Initial state identified by the PseudotimeKernel. d. Fate probabilities towards each identified terminal state based on the PseudotimeKernel (top) and VelocityKernel (bottom). The VelocityKernel does not identify the cDC terminal state. e. Log-transformed ratio of cross-boundary correctness of cell type transitions of the PseudotimeKernel and VelocityKernel (HSC: hematopoietic stem cell, MK/E prog: megakaryocyte/erythrocyte progenitors, G/M progenitor: Granulocyte/Myeloid progenitor, pDC: plasmacytoid dendritic cell, cDC2: classical dendritic cells). Values larger than zero correspond to the PseudotimeKernel outperforming the VelocityKernel; significance was tested using one-sided Welch’s t-tests (Methods). Box plots indicate the median (center line), interquartile range (hinges), and 1.5x interquartile range (whiskers) (HSC to pDC: N=62 cells, p = 0.12; HSC to cDC: N=38 cells, p = 0.11; HSC to G/M progenitor: N=659 cells, p = 1.48 × 10−15; G/M progenitor to CD14+ monocytes: N=435 cells, p = 2.51 × 10−9; HSC to MK/E prog: N=489 cells, p = 1.88 × 10−13; MK/E prog to proerythroblast: N=513 cells, p = 1.38 × 10−9; proerythroblast to erythroblast: N=1052 cells, p = 4.93 × 10−75; erythroblast to normoblast: N=499 cells, p = 1.19 × 10−10). f. The number of identified terminal states is plotted against the number of macrostates specified. In the optimal scenario (dashed black), a new terminal state is identified for every added macrostate. The terminal state identification score (TSI) is defined by the area under a given curve relative to the optimal identification (Methods).
Extended Data Fig. 4 Developing the CytoTRACEKernel.
a. Similar to the CytoTRACE publication18, we compute the CytoTRACE score by (i) calculating the number of genes expressed per cell (GEC), (ii) computing each gene’s Pearson correlation with GEC, (iii) mean-aggregating imputed expression of the top 200 correlated genes (Methods). Box plots indicate the median (center line), interquartile range (hinges), and 1.5x interquartile range (whiskers); the shown box plots are schematics. b. Force-directed layout embedding (FLE) of 22, 370 Caenorhabditis (C.) elegans muscle and mesoderm cells undergoing embryogenesis, colored by estimated embryo time78 (left; 130 − 830 minutes), CytoTRACE pseudotime computed using CellRank 2 (middle) and the original implementation (right). c. Quantitative comparison of the two implementations of the CytoTRACE pseudotime on bone marrow77 (using 10x and SmartSeq2), C. elegans embryogenesis78 (subsetted to ciliated neurons, hypodermis and seam, and muscle and mesoderm), and zebrafish embryogenesis79. The x axis (y axis) displays Spearman’s rank correlation between CellRank 2-CytoTRACE (original CytoTRACE) and ground-truth (GT) time labels. Ground-truth labels were derived from either embryo time or stages as in b. (C. elegans and zebrafish embryogenesis) or from manually assigned maturation labels from the original CytoTRACE study18 (bone marrow).
Extended Data Fig. 5 The CytoTRACEKernel recovers developmental progression, and terminal and initial states faithfully.
a. Distribution of pseudotimes from the CytoTRACEKernel (left), DPT (center), and Palantir (right), stratified by embryo stage (top row) and colored according to Fig. 3a. Box plots indicate the median (center line), interquartile range (hinges), and 1.5x interquartile range (whiskers) (E0-E3: N = 4574 cells, E6-E9: N = 7368 cells, E12-E15: N = 6241 cells, E18-E21: N = 6543 cells, E24-E27: N = 6302 cells); UMAP embeddings (bottom) are colored by pseudotime. b. Terminal states (left) and initial state (right) inferred using the CytoTRACEKernel.
Extended Data Fig. 6 Developing the RealTimeKernel.
a. Force-directed layout embedding (FLE) of 165, 892 mouse embryonic fibroblasts (MEFs) reprogramming towards various endpoints during an 18-day time course15, colored according to modified original annotations (IPS: induced pluripotent stem; left) or sequencing time points (right). Dotted (solid) circles indicate known initial (terminal) states. b. FLE showing simulated random walks from day 0 cells without (left; corresponds to WOT15) and with (right; corresponds to the RealTimeKernel) intra-time point transitions; black (yellow) dots denote a random walk’s start (end); green ticks (red crosses) indicate known terminal states that are (are not) explored by random walks. c. Initial state identified by the RealTimeKernel. d. Evaluation of the effect of thresholding the transition matrix in the RealTimeKernel. Each dot corresponds to one cell’s fate probability towards one of four terminal states, computed with thresholding (x axis) and without thresholding (y axis). The color coding is in agreement with a.e. Identification of terminal states with increasing number of macrostates using the VelocityKernel (CR 1; blue) or RealTimeKernel (CR2; orange).
Extended Data Fig. 7 The RealTimeKernel models fate decisions on a continuous domain.
a. Force-directed layout embedding (FLE) of 165, 892 mouse embryonic fibroblasts (MEFs) reprogramming towards various endpoints during an 18-day time course15, colored according to modified original annotations (IPS: induced pluripotent stem; left) or sequencing time points (right). Dotted (solid) circles indicate known initial (terminal) states. b,c. Violin plots showing pseudotime distribution for each of 36 experimental time points, using CellRank 2’s real-time-informed pseudotime (b.), DPT1 (c., left), or Palantir5 (c., right) (Methods). Box plots indicate the median (center line), interquartile range (hinges), and whiskers at 1.5x interquartile range. c. DPT1 (center), or Palantir5 (right) (Day 0: N = 4556 cells, Day 0.5: N = 3449 cells, Day 1: N = 3648 cells, Day 1.5: N = 1956 cells, Day 2: N = 6981 cells, Day 2.5: N = 6734 cells, Day 3: N = 6777 cells, Day 3.5: N = 7355 cells, Day 4: N = 8962 cells, Day 4.5: N = 7127 cells, Day 5: N = 7227 cells, Day 5.5: N = 6550 cells, Day 6: N = 8422 cells, Day 6.5: N = 3111 cells, Day 7: N = 6507 cells, Day 7.5: N = 5061 cells, Day 8: N = 3815 cells, Day 8.25: N = 3829 cells, Day 8.5: N = 3573 cells, Day 8.75: N = 3088 cells, Day 9: N = 2982 cells, Day 9.5: N = 2266 cells, Day 10: N = 2051 cells, Day 10.5: N = 1941 cells, Day 11: N = 2238 cells, Day 11.5: N = 2164 cells, Day 12: N = 2429 cells, Day 12.5: N = 2253 cells, Day 13: N = 2145 cells, Day 13.5: N = 2034 cells, Day 14: N = 3758 cells, Day 14.5: N = 2723 cells, Day 15: N = 3717 cells, Day 15.5: N = 4851 cells, Day 16: N = 3422 cells, Day 16.5: N = 4645 cells, Day 17: N = 3678 cells, Day 17.5: N = 4068 cells, Day 18: N = 3799 cells). d-g. Cell-specific fate change over pseudotime (RealTimeKernel, left) or experimental time (WOT, right) for the IPS (d.), neural (e.), stromal (f.), and trophoblast lineage (g.). For the RealTimeKernel, dashed vertical lines denote the mean pseudotime over all cells from a given experimental time point, recapitulating the correct ordering from b.
Extended Data Fig. 8 Initial and terminal state identification of pharyngeal endoderm development.
a. UMAP embedding of pharyngeal endoderm development dataset (left) and identified initial state population (right). Cells are colored according to cell types identified in the original study37. b. Identified number of terminal states with increasing number of macrostates using the full pharyngeal endoderm development dataset. c. UMAP embedding of subsetted pharyngeal endoderm dataset (right) and identified initial state (right); cells are colored according to the original study37. d. Same as b. but for the subsetted case.
Extended Data Fig. 9 Putative mTEC progenitors.
a. UMAP embedding of subsetted pharyngeal endoderm dataset; cells are colored according to the original study. b. The fate probabilities towards each terminal state are estimated using the RealTimeKernel. c. A cluster of putative mTEC progenitors is identified by cells with fate probabilities towards mTEC larger than 0.5. d. UMAP embedding colored by WOT’s pullback at E10.5 clipped to the 99 percentile. e. Gene ranking of potential mTEC drivers based on WOT’s pullback distribution at E11.5, compared to the gene ranking based on the pullback at E10.5, as shown in Fig. 4f. f. Gene ranking when performing classical differential expression analysis on clusters ‘mTEC progenitors’ and ‘Other progenitors’ as shown in c.
Extended Data Fig. 10 Terminal state analysis for metabolically labeled intestinal organoids.
a. UMAP embedding of intestinal cells colored according to their cell type (TA cells: transit-amplifying cells) according to the original publication9; black arrows indicate the known differentiation hierarchy. b. UMAP embedding highlighting terminal states identified with CellRank 1. c. Terminal state purity resulting from our metabolic-labeling-based vector field (CellRank 2) or classical RNA velocity (Cellrank 1). d. Terminal state identification using either CellRank 1 (CR 1) or CellRank 2 (CR 2) compared to an optimal identification (Optimal ident.) strategy. e. UMAP embedding highlighting terminal states identified by dynamo16. f. The ranking score metric for each method and terminal state. The metric quantifies the degree of optimality of a gene ranking compared to an optimal ranking. Dynamo only identified the trajectory leading up to enterocytes.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weiler, P., Lange, M., Klein, M. et al. CellRank 2: unified fate mapping in multiview single-cell data. Nat Methods 21, 1196–1205 (2024). https://doi.org/10.1038/s41592-024-02303-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41592-024-02303-9