Optimal transport for single-cell and spatial omics
单细胞和空间组学的最佳传输

Biological systems are dynamic at multiple scales, ranging from molecular and cellular to tissue, organ and organismal behaviour. At the cellular level, single-cell omics now provide a direct window into the molecular makeup of individual cells, which is both comprehensive and has high resolution, allowing us to capture a detailed snapshot of the molecular state of cells at a given point in time. Similarly, at the tissue level, advances in imaging and spatial omics help map cells and their molecular state as they are geometrically organized in tissues, improving our understanding of key physiological processes.
生物系统在多个尺度上都是动态的，涵盖从分子和细胞到组织、器官和生物体行为的各个层面。在细胞层面，单细胞组学如今提供了一个直接了解单个细胞分子组成的窗口，它不仅全面，而且分辨率高，使我们能够捕捉到特定时间点细胞分子状态的详细快照。同样，在组织层面，成像和空间组学的进步有助于绘制细胞及其在组织中几何排列的分子状态图，从而加深我们对关键生理过程的理解。

Although single-cell and spatial methods can now routinely generate millions of cell profiles, they do come with an important limitation: these methods are destructive assays, such that the same cell cannot be observed twice, and hence the resulting data are not aligned. This limitation has acute implications both for studying basic biological systems, from developmental biology to immunology, and in translational research, when we aim to monitor the response during pathogenesis or under treatment across multiple patients. Because of the destructive nature, the same cell cannot be profiled multiple times along a time course or measured using multiple modalities (unless they are measured simultaneously). In the case of single-cell technologies, physical dissociation of tissues also leads to loss of spatial information. To relate time points, modalities or positions require us to align and connect profiles collected from different cells post hoc.
尽管单细胞和空间方法现在可以常规生成数百万个细胞图谱，但它们也有一个重要的局限性：这些方法是破坏性测定，即无法对同一个细胞进行两次观察，因此得到的数据不一致。这种局限性对于研究从发育生物学到免疫学的基础生物系统以及在转化研究中（当我们旨在监测多个患者在发病过程中或治疗过程中的反应时）都具有严重的影响。由于破坏性，同一个细胞不能沿着时间进程进行多次分析，也不能使用多种模态进行测量（除非同时测量）。对于单细胞技术，组织的物理解离也会导致空间信息的丢失。为了关联时间点、模态或位置，我们需要事后对齐和连接从不同细胞收集的图谱。

The need to realign data sets is a common thread to all of these problems. Accordingly, a unifying mathematical framework, optimal transport (OT)^1,2, has emerged as an important solution. OT theory is a major research area in pure mathematics (see works by Villani¹, Figalli³ and Caffarelli⁴ for examples), which has been adopted as an approach to fill this gap in single-cell and spatial omics in silico. OT reconstructs how a source population (represented as one probability distribution) can morph efficiently into another target population, given only source and target samples. For example, if the source distribution is a sample of pre-stimulation cells, and the target is another sample of cells at some time point post-stimulation, OT can reconstruct the unobserved temporal process and provide an informed guess to recover an OT map relating the two cell populations and reconstructing the effect of the stimulation^5,6. With the development of deep learning parameterizations of OT, neural OT now allows us to predict how a perturbation might affect previously unseen cells — such as a different cell type stimulated in the same way or the cells of another patient with the same disease^6,7,8 — opening important opportunities in the field of precision medicine (Fig. 1).
重新调整数据集的需求是所有这些问题的共同点。因此，一个统一的数学框架， 最佳传输 （OT） ^{1、2 ，} 已成为重要的解决方案。OT 理论是纯数学中的一个主要研究领域（例如，参见 Villani ¹ 、Figalli ³ 和 Caffarelli ⁴ 的作品），它已被用作填补单细胞和空间组学计算机模拟中这一空白的方法。OT 重建了在仅给定源样本和目标样本的情况下，源群体（表示为一个概率分布）如何有效地转变为另一个目标群体。例如，如果源分布是刺激前细胞的样本，而目标是刺激后某个时间点的另一个细胞样本，则 OT 可以重建未观察到的时间过程并提供有根据的猜测来恢复与两个细胞群相关的 OT 图并重建刺激的效果 ^{5、6 。} 随着 OT 深度学习参数化的发展，神经 OT 现在使我们能够预测扰动如何影响以前未见过的细胞（例如以相同方式刺激的不同细胞类型或患有相同疾病的另一个患者的细胞 ^{6、7、8 ） ， 这}为精准医疗领域开辟了重要机遇（图 1 ）。

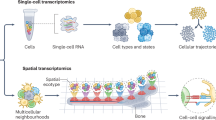
Optimal transport (OT) finds various use cases in single-cell biology. a, In the reconstruction of cellular differentiation processes in developmental biology, OT provides alignment among consecutive measurements and thus infers progenitors and descendants of each cell x. b, The re-alignment of single-cell measurements of each cell population before μ and after a perturbation ν, such as a treatment, chemical or genetic intervention. OT enables the reconstruction of fine-grained perturbation responses of heterogeneous cell populations^222,223,224. Parameterizing the OT with neural networks also allows the use of OT in predicting treatment outcomes of unseen cells, such as those from a new cell type or patient. c, OT can be employed to spatially reconstruct single-cell data. Given a reference atlas or spatially resolved single-cell measurements, OT is able to restore tissue geometries and architectures of single cells recorded using non-spatially-resolved measurement technologies. d, Advances in the development of high-throughput measurement technologies facilitate the recording of a biological system using different data modalities. OT can facilitate re-aligning measurements across modalities to provide a diverse characterization of similar cell states. RNA-seq, RNA sequencing.
最佳传输 (OT) 在单细胞生物学中有多种用途。a 、 在发育生物学中重建细胞分化过程时，OT 提供连续测量之间的比对，从而推断每个细胞 x 的祖细胞和后代 。b 、在 μ 之前和扰动 ν 之后（例如治疗、化学或基因干预）重新调整每个细胞群的单细胞测量值。OT 能够重建异质细胞^{群 222、223、224 的}细粒度扰动响应。使用神经网络参数化 OT 还允许使用 OT 预测看不见的细胞（例如来自新细胞类型或患者的细胞）的治疗结果 。c 、OT 可用于空间重建单细胞数据。给定参考图谱或空间分辨的单细胞测量值，OT 能够恢复使用非空间分辨测量技术记录的单细胞的组织几何形状和结构。 d 、高通量测量技术的进步促进了使用不同数据模式记录生物系统。OT 可以促进跨模式重新调整测量，从而提供相似细胞状态的多样化表征。RNA-seq，RNA 测序。

Full size image

In single-cell biology, OT has been used to infer the distributions of ancestors and descendants of cells along developmental processes⁵ (Fig. 1a), perform trajectory inference^{5,9,10,11,12,13,14,15,16}, predict perturbation responses^6,17,18 (Fig. 1b), spatially reconstruct the positions of cells in tissues^19,20 (Fig. 1c), integrate multi-omics data of different molecular modalities²¹ (Fig. 1d), infer cell–cell similarity²², integrate across scales or views (for example, in morphology and molecular profiling)²³ as well as missing modality imputation²⁴.
在单细胞生物学中，OT 已用于推断细胞祖先和后代在发育过程中的分布 ⁵ （图 1a ^{） ， 执行轨迹推断 5、9、10、11、12、13、14、15、16 ， 预测扰动响应 6、17、18 （} 图 1b），空间重建细胞在组织中的^{位置 19、20} （图 1c ），整合不同分子模态的多组学数据 ²¹ （ 图 1d ），推断细胞与细胞之间的相似性 ²² ，跨尺度或视图整合（例如，在形态学和分子分析中） ²³ 以及缺失模态插补 ²⁴ 。

The effectiveness of OT comes, however, with drawbacks: because the theory builds on sophisticated mathematics that blends optimization^25,26, stochastic differential equation (SDE)^11,16 and partial differential equation (PDE)⁹ and, more recently, deep learning^{6,7,13,18,23,27}, its computations are challenging even by modern machine-learning standards. Developing efficient algorithms for solving OT and its variations, as well as methodologies to make OT applicable to real-world problems, is a significant hurdle for wider adoption²⁸. This serves as the motivation of this Primer for a focused exploration of characteristics and unique potential of OT for single-cell and spatial omics.
然而，OT 在有效的同时也有缺点：因为该理论建立在融合了优化 ^{25、26 、} 随机微分方程 (SDE) ^{11、16 和}偏微分方程 (PDE) ⁹ 以及最近^{的深度学习 6、7、13、18、23、27 的复杂}数学基础之上，即使按照现代机器学习标准，其计算也具有挑战性。开发用于解决 OT 及其变体的有效算法，以及使 OT 适用于实际问题的方法是其广泛应用的重大障碍 ^28。 这成为本入门指南的动机，旨在重点探索 OT 在单细胞和空间组学中的特征和独特潜力。

In this Primer, we introduce the mathematical and computational principles of OT, to guide novel applications. We provide the reader with intuitive explanations of how seemingly unrelated mathematical approaches for analysing single-cell data can be unified through OT theory and how that theory has triggered recent advances in deep learning. We provide an overview of the broad range of biological applications, demonstrating the successes of OT in single-cell biology.
在本入门指南中，我们介绍了 OT 的数学和计算原理，以指导其创新应用。我们为读者提供直观的解释，解释如何通过 OT 理论统一看似毫不相关的单细胞数据分析数学方法，以及该理论如何推动深度学习的最新进展。我们概述了 OT 在生物学领域的广泛应用，并展示了其在单细胞生物学中的成功。

This section introduces the building blocks of OT theory, which we illustrate using representative examples from single-cell and spatial omics.
本节介绍 OT 理论的构成要素，我们使用单细胞和空间组学的代表性示例进行说明。

We first describe the mathematical concept of transport (before turning to the optimal qualifier). In mathematics, transport refers to the various ways to describe the transformation of one point cloud into another. In the simplest setting, these point clouds can describe several particles in the 3D physical space. In our case, such point clouds represent descriptors of high-dimensional data derived from single-cell or spatial omics as vectors in ${\mathbb{R}}^d$, in which d denotes the dimension of the data, determined by the number of genes or other biological features captured in the measured profile. To introduce the core concepts of OT, we introduce an example from single-cell biology.
我们首先描述迁移的数学概念（然后再转向最优限定词）。在数学中，迁移指的是描述一个点云到另一个点云变换的各种方式。在最简单的情况下，这些点云可以描述三维物理空间中的多个粒子。在我们的例子中，这些点云表示来自单细胞或空间组学的高维数据的描述符，作为 ${\mathbb{R}}^d$ 中的向量，其中 d 表示数据的维度，由测量曲线中捕获的基因或其他生物特征的数量决定。为了介绍迁移的核心概念，我们引入一个单细胞生物学的例子。

Example 1: reconstructing the temporal evolution of cell populations
示例 1：重建细胞群体的时间演变

Consider the responses over time of each cell in a (heterogeneous) cell population to a molecular stimulus or perturbation (such as a developmental or environmental signal, gene knockouts or drug treatment)^5,6. To study this process, a few thousand cells are sampled from a large population at each of several different time points along a time course and profiled using single-cell RNA sequencing (scRNA-seq). Because of the destructive nature of scRNA-seq, different cells are profiled at each time point. To model this process, each point x represents the recorded features of a single cell from scRNA-seq (Fig. 1a,b). Each feature (dimension) of that point x tracks the expression level of each studied gene in that cell at measurement time. Two consecutive snapshots can be seen as two point clouds or, alternatively, as two tabular data sets X = [x₁, …, x_n] and Y = [y₁, …, y_m]: each of the n or m rows contains a cell and its d-dimensional feature representation, in which each column denotes a particular feature, such as the expression level of a gene (Fig. 1a). To understand and reconstruct the temporal evolution of the cell population over time, or how cells in one time point transition to become the cells in a later time point, we aim to provide an informed guess on an alignment or a map that relates the two sets of cells X and Y.
考虑 (异质) 细胞群中每个细胞对分子刺激或扰动 (如发育或环境信号、基因敲除或药物治疗) 随时间的响应 ^{5、6 。} 为了研究这一过程，在时间过程中的几个不同时间点从大量细胞中取样数千个细胞，并使用单细胞 RNA 测序 (scRNA-seq) 进行分析。由于 scRNA-seq 的破坏性，每个时间点都会对不同的细胞进行分析。为了模拟这个过程，每个点 x 代表来自 scRNA-seq 的单个细胞的记录特征 (图 1a、b )。该点 x 的每个特征 (维度) 跟踪测量时该细胞中每个研究基因的表达水平。两个连续的快照可以看作两个点云，或者两个表格数据集 X = [ x ₁ , ..., x _n ] 和 Y = [ y ₁ , ..., y _m ]：其中 n 或 m 行中的每一行包含一个细胞及其 d 维特征表示，其中每一列表示一个特定特征，例如基因的表达水平（图 1a ）。为了理解和重建细胞群随时间的演变，或者一个时间点的细胞如何转变为稍后时间点的细胞，我们旨在对关联两组细胞 X 和 Y 的比对或图谱提供有根据的猜测。

Parameterizing transport  参数化传输

Defining a transport from data set X to Y is equivalent, intuitively, to associating, matching, aligning or mapping each of the elements in X to another in Y, similar to the case of cell profiles recorded at two different points in time resulting in measurement snapshots X and Y. Although there are countless ways to propose such associations, consider first a naive approach that does not usually result in a valid transport: suppose one associates to each point x_i in X its closest neighbour in Y according to some distance. Unfortunately, this approach will most often result in an unbalanced association (Fig. 2a), whereby some of the points y_j that are close to many points in X (relative to a distance or cost measure c) will be selected repeatedly, whereas those points y_j that are far away will not. In that case, cells from the earlier time point that differentiated during the time interval and show alterations in their molecular profile would not be aligned to any progenitor cell in the later time points. The notion of transport requires, intuitively, finding a balanced way in which all points in X are bijectively associated with points in Y.
直观地讲，定义从数据集 X 到 Y 的传输等同于将 X 中的每个元素关联、匹配、对齐或映射到 Y 中的另一个元素，类似于在两个不同时间点记录的细胞概况的情况，从而产生测量快照 X 和 Y 。尽管有无数种方法可以提出这种关联，但首先考虑一种通常不会产生有效传输的简单方法：假设一个人根据某个距离将 X 中的每个点 x 与 Y 中其最近的邻居关联起来。不幸的是，这种方法通常会导致不平衡的关联 （图 2a ），其中一些靠近 X 中的许多点（相对于距离或成本度量 c ）的点 y 将被重复选择，而那些距离较远的点 y 则不会。在这种情况下，来自较早时间点的细胞在时间间隔内分化并显示其分子概况发生变化，将不会与后期时间点的任何祖细胞对齐。直观地说，传输的概念要求找到一种平衡的方式，使 X 中的所有点都与 Y 中的点双射关联。

a, Assigning to each point x_i (for example, a single cell) its nearest neighbour y_j results in unbalanced assignments. b, To enforce a balanced matching, and when the number of points in each set is the same n = m, permutations are used to encode a one-to-one bijective matching. In that plot, σ is an arbitrary permutation, whereas σ^⋆ is that with the lowest cost. c, A natural extension for weighted point clouds, with respective weights a_i and b_j of the source and target distribution, of possibly different sizes n ≠ m is given by transportation plans P, or couplings with suitable marginals. P^⋆ refers to the optimal transport plan. d, Moving towards the continuous setting, in which both measures μ and ν have a density, the variable of interest becomes a pushforward map, that is able to reconstruct ν by applying a map T (or the optimal transport map T^⋆) to all the points in the support of measure μ. Across all panels, red and blue represent the source and target distributions, respectively.
a 、将每个点 x （例如，单个单元格）分配给其最近邻 y 会导致分配不平衡。 b 、为了强制平衡匹配，并且当每组中的点数相同 n = m 时，使用排列来编码一对一的双射匹配。在该图中， σ 是任意排列，而 σ ^⋆ 是成本最低的排列。 c 、加权点云的自然延伸，源和目标分布的权重分别为 a 和 b ，可能大小不同 n ≠ m ， ^由运输计划 P 或具有合适边际的耦合给出。P ⋆ 指最佳运输计划。d 、 转向连续设置，其中度量 μ 和 ν 都具有密度，感兴趣的变量变成前推图，能够通过将图 T （或最佳运输图 T ^⋆ ）应用于度量 μ 支持下的所有点来重建 ν 。在所有面板中，红色和蓝色分别代表源分布和目标分布。

Full size image

One-to-one matchings  一对一匹配

The simplest transport model to go from X to Y can occur when n = m, in which case it can be parameterized as a one-to-one matching. Such matching can be encoded through a permutation σ in the set ${\mathcal{S}}_n$ of permutations of size n, of which there are n!. Intuitively, a permutation is a list (σ₁, …, σ_n), in which each of the n integers from 1 to n appears exactly once, rearranged in any arbitrary order. A permutation is then interpreted as stating that the ith element of X is associated to the σ_ith element in Y, in which the point x_i is tied with $y_{{\text{σ}}_i}$. Permutations enforce that all points in X are associated with all points in Y and vice versa, using the inverse permutation σ⁻¹ (Fig. 2b), in that each progenitor cell from an earlier time point is mapped to one descendant cell recorded at a later time point or after a perturbation has occurred. At a more conceptual level, permutations are bijections from and to the set {1, …, n}, and there are exactly n! of them.
从 X 到 Y 的最简单的传输模型可能发生在 n = m 时，在这种情况下它可以被参数化为一对一匹配 。这种匹配可以通过在大小为 n 的排列集合 ${\mathcal{S}}_n$ 中的排列 σ 进行编码，其中有 n ！直观地讲，排列是一个列表 ( σ ₁ , ..., σ _n )，其中从 1 到 n 的 n 个整数中的每一个都出现一次，以任意顺序重新排列。然后，排列被解释为表明 X 中的第 i 个元素与 Y 中的第 σ 个元素相关联，其中点 x 与 $y_{{\text{σ}}_i}$ 相关联。置换强制 X 中的所有点与 Y 中的所有点相关联，反之亦然，使用逆置换 σ ⁻¹ （图 2b ），其中来自较早时间点的每个祖细胞都会映射到在较晚时间点或发生扰动后记录的一个后代细胞。从更概念化的层面来看，置换是从集合 {1, …, n } 到集合 {1, …, n } 的双射，并且恰好有 n ! 个。

Transportation plans  交通计划

Although intuitive and simple, permutations cannot be used if the number of points in X and Y is different, namely, n ≠ m. This limitation is particularly relevant in the context of biological examples, in which various factors contribute to different numbers of points in data sets X and Y. Technically, the discrepancy could be attributed to variations in the number of cells profiled. More fundamentally, biological processes are governed by events such as cell division at different rates along differentiation. Additionally, the nature of the data resembles a fate map rather than a lineage; cells in differentiation processes have multiple non-zero probabilities of transforming into different fates, with only one being realized. This makes the direct application of permutations unsuitable for capturing the intricacies of such biological phenomena and, more generally, to model a transport between weighted point clouds, in which a probability weight a_i > 0 (respectively b_j) is associated with each point x_i in X (respectively y_j in Y). A natural generalization for permutations can be found in n × m rectangular coupling matrices P, or transport plan. Each entry P_ij describes whether a point x_i is matched to point y_j. The entry is 0 when there is no association, but, rather than indicating by a binary 1 whether x_i is associated to y_j, the value in P_ij quantifies an association strength, namely, how much of the weight of point x_i is transferred to y_j (Fig. 2c). When computing a coupling between two snapshots of single-cell measurements, it provides a probabilistic assignment of which progenitor cell would most likely transform into which descendant cell. This is roughly analogous to a cell fate map (but not a lineage map, which is by definition deterministic and is irrelevant here because the measurements are destructive, such that no progenitor cell had any real descendants). To ensure that all masses are conserved, entries of P should be non-negative and such that P1_m = a and $P{\mathbf{1}}_n^T=b$. The set of admissible matrices is then denoted as
尽管排列直观简单，但如果 X 和 Y 中的点数不同，即 n ≠ m ，则无法使用排列。这种限制在生物学示例中尤其重要，因为各种因素会导致数据集 X 和 Y 中的点数不同。从技术上讲，这种差异可以归因于所分析的细胞数量的变化。更根本的是，生物过程受细胞分裂等事件的支配，这些事件沿着分化过程以不同的速率进行。此外，数据的性质更像是命运图而不是谱系；分化过程中的细胞具有转变为不同命运的多个非零概率，但只有一个能够实现。这使得直接应用排列不适合捕捉此类生物现象的复杂性，更一般地说，不适合模拟加权点云之间的传输，其中概率权重 a > 0（分别为 b ）与 X 中的每个点 x （分别为 Y 中的 y ）相关联。置换的自然推广可以在 n × m 矩形耦合矩阵 P （或称迁移规划） 中找到。每个元素 P _{i j} 描述点 x 是否与点 y 匹配。 当没有关联时，条目为 0，但是， P _{i j} 中的值不是用二进制 1 表示 x 是否与 y 关联，而是量化关联强度，即点 x 的权重有多少转移到 y （图 2c ）。在计算两个单细胞测量快照之间的耦合时，它提供了一个概率分配，即哪个祖细胞最有可能转化为哪个后代细胞。这大致类似于细胞命运图（但不是谱系图，谱系图根据定义是确定性的，并且在这里无关紧要，因为测量是破坏性的，因此没有祖细胞有任何真正的后代）。为了确保所有质量都守恒， P 的条目应该是非负的，并且 P 1 _m = a 和 $P{\mathbf{1}}_n^T=b$ 。然后，可接受矩阵集表示为

Pushforward maps  推进地图

Yet another conceptual leap in the OT theory can be achieved by moving from discrete formulations to the continuous regime. Here, point clouds X and Y become intuitively of infinite size and give way to probability measures $\mu ,\nu \in \mathcal{P}({\mathbb{R}}^d)$ (Fig. 2d). Now, measurements X and Y are simply realizations of the underlying distribution μ (the distribution over cellular states at one time point) and ν (the distribution of cell states at a later time point). The permutations that were useful to parameterize one-to-one mappings for point clouds of equal size have their counterpart in the more advanced notion of pushforward map, or maps $T:{\mathbb{R}}^d\to {\mathbb{R}}^d$ that are such that T♯μ = ν, in which ♯ is the pushforward operator (Box 1). The transport mapT describes, for example, a perturbation effect, as in how an unperturbed population μ responds and evolves into the perturbed population ν = T♯μ (Fig. 1b).
OT 理论的另一个概念飞跃可以通过从离散公式转向连续形式来实现。此时，点云 X 和 Y 直观上变为无限大，并让位于概率测度 $\mu ,\nu \in \mathcal{P}({\mathbb{R}}^d)$ （图 2d ）。现在，测量值 X 和 Y 仅仅是底层分布 μ （某一时间点的细胞状态分布）和 ν （后续时间点的细胞状态分布）的实现。用于参数化等大小点云一对一映射的置换在更高级的概念 “前推图” 中可以找到对应，即满足 T♯ μ = ν 的映射 $T:{\mathbb{R}}^d\to {\mathbb{R}}^d$ ，其中 ♯ 是前推算子（框 1 ）。例如， 传输图 T 描述了一种扰动效应，即未受扰动的种群 μ 如何响应并演化为受扰动的种群 ν = T♯ μ （图 1b ）。

Evaluating a transport cost
评估运输成本

Through either a permutation, a coupling matrix or a pushforward map, we have defined in the previous section valid ways to transport a (weighted) point cloud or a probability distribution into another predefined configuration. For each of these scenarios, assuming there is a choice of possible maps, what would constitute a good or efficient transport is determined. Here, a good or efficient transport is one that proposes a meaningful alignment between different measurements.
在上一节中，我们定义了通过置换、耦合矩阵或前推映射，将（加权）点云或概率分布传输到另一个预定义配置的有效方法。对于每种情况，假设存在多种可能的映射，则需要确定一种良好或高效的传输方式。在这里，良好或高效的传输是指能够在不同测量结果之间建立有意义的对齐的传输方式。

To define a notion of efficiency, we rely on a cost function c between a pair of points to derive various objective functions, one for each of the ways we have defined transport. Concretely, we need to select a cost function for which, based on their molecular features, cells are aligned to their most likely cell state in the subsequent measurement. Although one can use Euclidean distances for low-dimensional data or cosine²⁹ or correlation-based distances³⁰ for RNA-seq data, robust choices of cost metrics are active areas of research^31,32,33,34.
为了定义效率的概念，我们依赖一对点之间的成本函数 c 来推导各种目标函数，每种目标函数对应我们定义的传输方式。具体来说，我们需要选择一个成本函数，根据细胞的分子特征，将细胞与其在后续测量中最可能的细胞状态对齐。虽然低维数据可以使用欧氏距离，RNA 测序数据可以使用余弦距离 ²⁹ 或基于相关性的距离 ³⁰ ，但稳健的成本指标选择仍然是当前研究^{的热点 31、32、33、34 。}

In the case of permutations, a natural global cost $\mathcal{C}$ computed from local costs between pairs of matched points can be defined by comparing matched points, as
对于排列，可以通过比较匹配点来定义由匹配点对之间的局部成本计算出的自然全局成本 $\mathcal{C}$ ，如下所示

The natural extension of this idea when transporting mass between weighted point clouds yields a sum of costs between pairs, weighted by the amount transferred between these two points:
当在加权点云之间传输质量时，这个想法的自然延伸会产生对之间的成本总和，该总和由这两点之间传输的量加权：

The resulting cost can be interpreted as a quantification, or distributional distance, between the two point clouds μ and ν. Besides the plan P itself, the OT distance:
最终的成本可以解释为两个点云 μ 和 ν 之间的量化或分布距离。除了规划 P 本身之外，OT 距离：

is an important quantity used in the analysis of single-cell or spatial omics. It is also often employed as a loss function in machine-learning applications to quantify how close the output distribution of a model resembles the data set used to train the model.
是单细胞或空间组学分析中的一个重要参数。它也常被用作机器学习应用中的损失函数，以量化模型输出分布与用于训练模型的数据集的相似程度。

A natural objective for a pushforward transport map T from ${\mathbb{R}}^d$ to ${\mathbb{R}}^d$ is given by the integral:
从 ${\mathbb{R}}^d$ 到 ${\mathbb{R}}^d$ 的前推传输图 T 的自然目标由积分给出：

That integral blends elements from both costs mentioned earlier, borrowing from equation (2) the idea of comparing each point x with the point T(x) it is mapped to, while also incorporating mass considerations as that cost is weighted by the mass μ at x. Equation (5) represents the famous Monge³⁵ formulation of OT.
该积分融合了前面提到的两种成本的元素，借鉴了方程 ( 2 ) 中将每个点 x 与其映射到的点 T ( x ) 进行比较的思想，同时还融入了质量的考虑因素，因为该成本由 x 处的质量 μ 加权。方程 ( 5 ) 代表了著名的 Monge ³⁵ OT 公式。

Although using the same notation $\mathcal{C}$ for all three formulas mentioned earlier might be seen as a slight abuse of notation, we do so because this highlights the unifying idea of summing — with either single-indexed or double-indexed sums, or with integrals — granular contributions brought by costs computed between pairs of points.
尽管对前面提到的所有三个公式使用相同的符号 $\mathcal{C}$ 可能被视为对符号的轻微滥用，但我们这样做是因为这突出了求和的统一思想——使用单指标或双指标总和，或使用积分——由点对之间计算的成本带来的细粒度贡献。

Finding an optimal transport
寻找最佳运输方式

Computational OT is the field concerned with efficiently finding a transport, which can either be a permutation σ, a coupling matrix P or a map T, that has a low cost $\mathcal{C}$. In each of these three cases, minimizing $\mathcal{C}$ results in a constrained optimization problem. These problems are, respectively, known in the literature as the optimal assignment, the Kantorovich³⁶ and the Monge³⁵ problems. This search creates a host of challenges that we briefly survey. We first describe exact methods, which aim to probably find the best possible transport. Because of the computational challenges faced by these methods, we next introduce various approaches that rely instead on regularization and/or neural network parameterizations to obtain approximate yet tractable solutions.
计算 OT 是研究如何高效地找到一种传输方式的领域，这种传输方式可以是排列 σ 、耦合矩阵 P 或映射 T ，且具有较低的成本 $\mathcal{C}$ 。在这三种情况下，最小化 $\mathcal{C}$ 都会导致一个受约束的优化问题 。在文献中，这些问题分别被称为最优分配、Kantorovich ^{36 问题}和 Monge ³⁵ 问题。这种探索带来了一系列挑战，我们将对其进行简要概述。我们首先描述精确的方法，旨在找到最佳的传输方式。由于这些方法面临的计算挑战，接下来我们将介绍各种依赖于正则化和/或神经网络参数化的方法来获得近似但易于处理的解决方案。

Solving optimal transport exactly
精确求解最优传输

Finding a permutation σ that minimizes equation (2) or a coupling P for equation (3) is the seminal optimization problem, appearing as early as the first half of the twentieth century. The former can be solved with the Hungarian algorithm³⁷, with a worst-case complexity scaling as O(n³). The latter is widely recognized as a central piece of optimization theory, which provided the impetus for the entire field of linear programming³⁸. The problem of finding an optimal coupling P was formulated by Hitchcock³⁹, Kantorovich³⁶ and Koopmans⁴⁰ (Box 2). Most computational approaches solving it rely on variants of the network simplex⁴¹ or the auction algorithm⁴², with computational cost $O(nm(n+m)\log (n+m))$. That cubic cost is often prohibitive for large-scale applications. In addition, these algorithms can be difficult to implement on parallel architectures, such as GPUs, because they involve sequential discrete selections, such as the pivot rule in the simplex.
寻找使方程 ( 2 ) 最小化的排列 σ 或方程 ( 3 ) 的耦合 P 是一个开创性的优化问题，早在二十世纪上半叶就出现了。前者可以用匈牙利算法 ³⁷ 求解，最坏情况复杂度为 O ( n3 )。后者被广泛认为是^最优化理论的核心部分，它为整个线性规划领域 ³⁸ 提供了推动力。寻找最优耦合 P 的问题由 Hitchcock ³⁹ 、Kantorovich ³⁶ 和 Koopmans ⁴⁰ （框 2 ）提出。大多数解决该问题的计算方法依赖于网络单纯形 ⁴¹ 或拍卖算法 ⁴² 的变体，计算成本为 $O(nm(n+m)\log (n+m))$ 。对于大规模应用来说，这种立方成本通常是过高的。此外，这些算法很难在并行架构（如 GPU）上实现，因为它们涉及顺序离散选择，例如单纯形中的枢轴规则。

Because it requires optimizing over functions, while handling a non-convex pushforward constraint, equation (5) is much harder to solve in practice. Given two probability measures μ and ν, the feasible set of maps that can push forward μ to ν is not convex, making the toolbox of convex optimization irrelevant. In the common case in which the cost between two points is the squared-Euclidean distance, c(x, y) = ∥x − y∥², two approaches have been proposed. The first approach, proposed by Benamou and Brenier⁴³, re-parameterizes the OT problem by introducing a discrete sequence μ_k of measures, for 0 ≤k ≤T, that interpolates, using the convention μ₀ ≔ μ and μ_T ≔ ν, between the two measures to be compared. Using another discretization (in space), this method proposes to parameterize OT using the continuity equation (13) and advection of velocity fields v_t. Its main innovation is to re-parameterize the problem of minimizing the total kinetic energy needed to realize that sequence (itself equal to the total Euclidean cost) as a function of (μ_tv_t, μ_t) rather than (μ_t, v_t) to recover a convex problem. This requires, however, a discretization not only in time t but also in space, which is only tractable for low-dimensional problems. The second approach relies on exploiting Brenier’s theorem⁴⁴ (Box 3) to reframe the OT problem as a PDE problem, known as the Monge–Ampère equation³. Because both approaches require a grid discretization on the space of observations, they can only be implemented when observations are low-dimensional, making them unsuitable for the high-dimensional problems of single-cell and spatial omics. However, as we show in the next section, Brenier’s theorem⁴⁴ (Box 3) does play an important role in neural network-inspired approaches as well as in dynamic formulations of OT.
由于需要对函数进行优化，同时处理非凸的前推约束，方程 ( 5 ) 在实践中更难求解。给定两个概率测度 μ 和 ν ，可以将 μ 前推到 ν 的可行映射集不是凸的，因此凸优化工具箱变得无关紧要。在两点之间的成本是平方欧几里得距离的常见情况下， c ( x , y ) = ∥ x − y ∥ ² ，已提出了两种方法。第一种方法由 Benamou 和 Brenier ⁴³ 提出，通过引入一个离散的测度序列 μ _k （其中 0 ≤ k ≤ T ）重新参数化 OT 问题，使用约定 μ ₀ ≔ μ 和 μ _T ≔ ν 在两个要比较的测度之间进行插值。该方法采用另一种空间离散化方法，提出使用连续性方程 ( 13 ) 和速度场平流 v _t 来参数化 OT。其主要创新之处在于，将最小化实现该序列所需的总动能（本身等于总欧氏成本）的问题重新参数化为 ( μ _t v _t , μ _t ) 的函数，而不是 ( μ _t , v _t ) 的函数，从而恢复凸问题。 然而，这不仅需要在时间 t 上离散化，还需要在空间上离散化，而这只适用于低维问题。第二种方法依赖于利用 Brenier 定理 ⁴⁴ （框 3 ）将 OT 问题重新定义为 PDE 问题，即 Monge-Ampère 方程 ³ 。由于这两种方法都需要在观测空间上进行网格离散化，因此它们只能在观测值为低维时实现，这使得它们不适用于单细胞和空间组学的高维问题。然而，正如我们在下一节中所示，Brenier 定理 ⁴⁴ （框 3 ）在神经网络启发方法以及 OT 的动态公式中确实发挥着重要作用。

Data-driven optimal transport solvers
数据驱动的最优传输求解器

Equations (2), (3) and (5) provide an intuitive formalism to solving OT problems, but yield intractable computations when used in practice with large sample sizes (n ≥ 10³) or high-dimensional (d ≫ 3) data, both settings being the working assumption of single-cell and spatial omics. This has led to several proposals, focusing on the Kantorovich and Monge problems, to compute efficiently an n × m coupling matrix between samples, or a map ${\mathbb{R}}^d\to {\mathbb{R}}^d$.
方程 ( 2 )、( 3 ) 和 ( 5 ) 为解决 OT 问题提供了一种直观的形式化方法，但在实际处理大样本量（ n ≥ ¹⁰³ ）或高维数据（ d≫3 ）时，会产生难以处理的计算，而这两种情况都是单细胞和空间组学的工作假设。这导致了多项提案的提出，这些提案主要针对 Kantorovich 问题和 Monge 问题，旨在高效地计算样本之间的 n × m 耦合矩阵，或映射 ${\mathbb{R}}^d\to {\mathbb{R}}^d$ 。

Solvers to compute coupling matrices
计算耦合矩阵的求解器

Although linear programme solvers can be used to solve equation (3), they scale poorly as n grows. Instead, most solvers currently in use output an approximate solution using penalized approaches. Among those, entropic regularization²⁵ is arguably the most popular approach, because it relies on the Sinkhorn algorithm, a fixed-point iteration that only uses matrix–vector products (Box 4). This algorithm can also yield estimators for the OT map T(5), as presented in the next section.
虽然线性规划求解器可以用来求解方程 ( 3 )，但它们的扩展性随着 n 的增长而变差。目前使用的大多数求解器都使用惩罚方法输出近似解。其中，熵正则化 ²⁵ 可以说是最流行的方法，因为它依赖于 Sinkhorn 算法，这是一种仅使用矩阵向量积的定点迭代算法（框 4 ）。该算法还可以为 OT 映射 T ( 5 ) 提供估计量，如下一节所述。

A more recent strand of solvers relies on low-rank approximations of both cost and coupling matrices^45,46, by parameterizing variable P as the product of three matrices QD(1/g)R^T of respective sizes n × r, r × r and r × m. Although harder to implement than the Sinkhorn algorithm, these solvers have the favourable property that their runtime becomes linear in the size of point clouds, under the assumptions that the rank d of cost matrices is small compared with sample sizes and the restriction that only couplings of rank r are considered. Although the former assumption is often observed as the rank of a pairwise squared-Euclidean distance matrix between n and m points in ${\mathbb{R}}^d$ is at most d + 2, restricting optimization to couplings of rank r induces solutions that intuitively restrict the displacement of mass between two point clouds to move through r intermediary hubs⁴⁶, which might recover hierarchical structures such as cell types present in the aligned data⁴⁷.
较新的一类求解器依赖于成本矩阵和耦合矩阵的低秩^{近似 45、46} ，通过将变量 P 参数化为三个矩阵 QD (1/ g ) RT 的乘积 ^， 其大小分别为 n × r 、 r × r 和 r × m 。虽然比 Sinkhorn 算法更难实现， 但它们具有良好的特性，即在成本矩阵的秩 d 小于样本大小的假设以及仅考虑秩为 r 的耦合的限制下，它们的运行时间与点云的大小呈线性关系。尽管前一种假设通常被观察到为 ${\mathbb{R}}^d$ 中 n 和 m 点之间的成对平方欧几里得距离矩阵的秩最多为 d + 2，但将优化限制为秩为 r 的耦合会诱导直观地限制两个点云之间的质量位移通过 r 个中间中心 ^{46 的}解决方案，这可能会恢复对齐数据 ⁴⁷ 中存在的层次结构（例如细胞类型）。

Solvers to compute transport maps
用于计算传输图的求解器

The exact and data-driven solvers to compute coupling matrices we described earlier cannot operate on unseen samples: they only return an alignment or coupling of those data points initially considered in the computation. Conversely, if we, for example, wish to infer the descendants of an unseen sample or data set, or predict the effect of a drug on new cells from a different patient, we need solvers that act out-of-sample. In addition to that computational shortcoming, the solvers mentioned earlier have a statistical flaw, as approaches based on discrete samples, such as equation (3), tend to overfit data, leveraging information from finite samples to the extent that such couplings do not generalize well to new points⁴⁸ because of the curse of dimensionality⁴⁹.
我们之前描述的用于计算耦合矩阵的精确和数据驱动的求解器无法对未见过的样本进行操作：它们仅返回计算中最初考虑的数据点的对齐或耦合。相反，如果我们希望推断未见过的样本或数据集的后代，或者预测药物对不同患者的新细胞的影响，则需要样本外求解器。除了计算上的缺陷之外，前面提到的求解器还存在统计缺陷，因为基于离散样本的方法（例如公式 ( 3 )）往往会过度拟合数据，利用有限样本中的信息，以至于由于维数灾难 ⁴⁹ ，这种耦合不能很好地推广到新点 ⁴⁸ 。

Concretely, when looking for a map T that solves equation (5) for a pair of measures μ, ν and a cost function c, the challenge is to work out, from samples x₁, …, x_n ~ μ and y₁, …, y_m ~ ν, a function $\hat{T}:{\mathbb{R}}^d\to {\mathbb{R}}^d$ that provides a plausible substitute for T^⋆.
具体来说，当寻找一个映射 T 来求解方程 ( 5 ) 中一对测度 μ 、 ν 和一个成本函数 c 时 ，挑战在于从样本 x ₁ , ..., x _n ~ μ 和 y ₁ , ..., y _m ~ ν 中找出一个函数 $\hat{T}:{\mathbb{R}}^d\to {\mathbb{R}}^d$ 来为 T ^⋆ 提供合理的替代品。

The benefit of such an approach is to recover a function that can generalize to new points, rather than just obtain a matching matrix between existing samples. In that context, two main approaches stand out.
这种方法的好处是恢复一个可以推广到新点的函数，而不仅仅是获得现有样本之间的匹配矩阵。在这方面，有两种主要方法脱颖而出。

The first approach extends the estimates produced by Sinkhorn solvers (Box 4) out-of-sample, owing to duality² (Box 2). In brief, using point clouds (x₁, …, x_n) and (y₁, …, y_m), compared through cost function c, this approach consists in solving first equation (19) to recover the two dual variables ${\alpha }^{\star }\in {\mathbb{R}}^n,{\beta }^{\star }\in {\mathbb{R}}^m$ that are fixed points of equation (21). These two vectors α^⋆, β^⋆ contain n + m values, one for each of the x and y points contained in the source (x₁, …, x_n) and target (y₁, …, y_m) distributions. The following formulas^31,50,51 can be used to extend these values to out-of-sample points:
第一种方法将 Sinkhorn 求解器（框 4 ）产生的估计值扩展到样本外， _这是由于对偶性 ² （框 2 ）造成的。简而言之，使用点云（ x1 ，...， xn ）和 _（ y1 ， _...，ym ） ，通过成本函数 _c 进行比较，该方法包括求解第一个方程（ 19 ）以恢复两个对偶变量 ${\alpha }^{\star }\in {\mathbb{R}}^n,{\beta }^{\star }\in {\mathbb{R}}^m$ ， ^它们是方程（ 21 ） _的不动点。这两个向量 α⋆ ^， β⋆ 包含 n + m 个值，源（ x1 ，...， xn _） 和目标（ _y1 ，...， ym _） 分布中包含的每个 x 和 y 点都有一个值 。 ^{以下公式 31、50、51} 可用于将这些值扩展到样本外点：

which can then be plugged into a generalized Brenier-type formula⁵², to recover in full generality
然后可以将其代入广义的 Brenier 型公式 ⁵² 中，以完全恢复一般性

This formula requires invertibility concerning the second variable, of the map ∇₁c(x, ⋅) at any x, a condition often referred to as the twist condition. This formula is of course notably simpler for common costs c. For instance, when the cost is the squared Euclidean cost, this recovers
该公式要求映射 ∇ ₁ c ( x , ⋅ ) 的第二个变量在任意 x 处具有可逆性，这一条件通常被称为扭转条件 。当然，对于常见的成本 c 来说，这个公式要简单得多。例如，当成本是欧几里得成本的平方时，公式可以恢复

in which $p_j(x):=\frac{b_j{e}^{({\beta }_j^{\star }-\parallel x-y_j{\parallel }^2)/\text{ε}}}{{\sum }_{k=1}^m{b}_k{e}^{({\beta }_k^{\star }-\parallel x-y_k{\parallel }^2)/\text{ε}}}$ can be interpreted as a discrete Gibbs distribution, depending on x, using values ${\beta }_k^{\star }-\parallel x-y_k{\parallel }^2$ and temperature ε.
其中 $p_j(x):=\frac{b_j{e}^{({\beta }_j^{\star }-\parallel x-y_j{\parallel }^2)/\text{ε}}}{{\sum }_{k=1}^m{b}_k{e}^{({\beta }_k^{\star }-\parallel x-y_k{\parallel }^2)/\text{ε}}}$ 可解释为离散吉布斯分布，取决于 x ，使用值 ${\beta }_k^{\star }-\parallel x-y_k{\parallel }^2$ 和温度 ε 。

The second approach is based on neural networks. Finding a function T that approximately maps a distribution onto another, that is, T♯μ = ν, using samples from both measures is a fundamental task in machine learning that is often handled using neural networks. Here, approaches diverge based on two different scenarios. In the supervised setup, in which paired samples from a coupling for μ, ν are given, that is, input–output pairs (x_i, y_i), estimating such maps T requires minimizing an empirical reconstruction loss, as in ℓ(y_i, T(x_i)). OT methods tackle, on the contrary, the more ambitious and somewhat only partially supervised setting, in which unpaired data sets ${(x_i)}_i$ and ${(y_j)}_j$ are given. Such problems have been described in the past as generative modelling problems^53,54, or alternatively as normalizing flows and variants⁵⁵, notably when either of these measures is simple to sample from. In that sense, OT provides some novelty. From a descriptive perspective, OT maps do more than simply push forward a measure onto another; they should in principle be the best of such maps. And, it is by asking that extra requirement that we can get, in exchange, a useful inductive bias to guide the selection of these maps. That bias is given more precisely by Brenier’s theorem⁴⁴, which has led refs. ^56,57 to parameterize OT maps as gradients of neural networks^6,9,58,59, or directly as a vector-valued neural network⁷ using a regularizer.
第二种方法基于神经网络。使用来自两个度量的样本，找到一个将一个分布近似映射到另一个分布的函数 T ，即 T♯ μ = ν ，是机器学习中的基本任务，通常使用神经网络来处理。在这里，方法根据两种不同的情况而有所不同。在监督设置中，给定来自 μ ， ν 的耦合的配对样本，即输入输出对 ( x , y )，估计这样的映射 T 需要最小化经验重建损失，如 ℓ ( y , T ( x ) )。相反，OT 方法处理的是更具挑战性且仅部分监督的设置，其中给定未配对的数据集 ${(x_i)}_i$ 和 ${(y_j)}_j$ 。过去，此类问题被描述为生成建模^{问题 53、54} ，或者称为规范化流和变体 ⁵⁵ ，特别是当其中任何一个度量都易于采样时。从这个意义上说，OT 提供了一些新颖之处。从描述性的角度来看，OT 映射不仅仅是简单地将一个测度推到另一个测度上；原则上，它们应该是此类映射中最好的。而且，正是通过提出这个额外的要求，我们才能获得一个有用的归纳偏差来指导这些映射的选择。这种偏差由 Brenier 定理 ⁴⁴ 更精确地给出，该定理引发了文献[2]。 ^{56、57 将} OT 图参数化为神经^{网络 6、9、58、59 的梯度} ，或直接使用正则化器将其参数化为向量值神经网络 ⁷ 。

Extensions of optimal transport
最优传输的扩展

So far, we have considered standard formulations of OT, illustrated using the example of modelling cell differentiation into various cell lineages or how cell populations respond to perturbations. However, several key characteristics of biological systems require adaptations of classical OT, including allowing for cell division, migration and death, integrating different data modalities or tracking cellular responses continuously in time. In the following, we introduce extensions of OT that can capture these characteristics.
到目前为止，我们已经探讨了场理论（OT）的标准公式，并以模拟细胞分化成各种细胞谱系或细胞群体如何响应扰动为例进行了说明。然而，生物系统的几个关键特性需要对经典场理论进行调整，包括允许细胞分裂、迁移和死亡，整合不同的数据模式，或持续跟踪细胞随时间的变化。接下来，我们将介绍能够捕捉这些特性的场理论的扩展。

Partial matchings  部分匹配

The conservation of mass principle is fundamental to all definitions of OT mentioned earlier and distinguishes it from simpler nearest-neighbour-based matching approaches or from attention mechanisms in transformers⁶⁰. It is, however, possible to escape that binary view and introduce a gradual approach to parameterize the degree to which one expects a coupling P or a map T to obey that constraint. This provides greater flexibility when modelling cellular dynamics that are subject to birth (from division or migration) and death events^5,18,61,62 or data sets that contain different numbers of measurements²¹.
质量守恒原理是前面提到的所有 OT 定义的基础，并将其与更简单的基于最近邻的匹配方法或 Transformer 中的注意机制 ^{60 区}分开来。然而，可以摆脱这种二元视图，并引入一种渐进的方法来参数化人们期望耦合 P 或映射 T 遵守该约束的程度。这在模拟受出生（分裂或迁移）和^{死亡事件 5、18、61、62 或}包含不同测量次数 ²¹ 的数据集影响的细胞动力学时提供了更大的灵活性。

The key insight in such approaches is to relax and dualize such mass conservation laws (Box 2). In the case of couplings (equation (3)), this can be achieved by dropping the feasible set (1) and adding to the objective a multiple of Δ(P1_m∣a) and Δ(P^T1_n∣b), in which Δ is a discrepancy function quantifying the difference between two unnormalized distributions^63,64. A notable case is given when Δ is the Kullback–Leibler divergence, because of its natural connections with the entropic regularization presented in equation (19). Indeed, rewriting the objective in equation (19) as a Kullback–Leibler divergence itself, one can define the unbalanced entropic transport objective as
此类方法的关键在于放宽并二元化此类质量守恒定律（框 2 ）。对于耦合（方程 ( 3 )），可以通过删除可行集 ( 1 ) 并在目标函数中添加 Δ ( P1m∣a ) 和 Δ( P1n∣b ) 的倍数来实现，其中 Δ 是量化两个^非正_则化分布之间差异的差异函数 ^{63、64 。} 一个值得注意的例子是 Δ 是 Kullback-Leibler 散度，因为_它与方程 ( 19 ) 中提出的熵正则化有着天然的联系。事实上，将方程 ( 19 ) 中的目标函数重写为 Kullback-Leibler 散度本身，就可以将不平衡熵传输目标定义为

which can be solved using a minor modification of the Sinkhorn algorithm, in which the updates in equation (20) have an extra element-wise exponential operation,
这可以使用对 Sinkhorn 算法稍加修改来求解，其中方程 ( 20 ) 中的更新具有额外的逐元素指数运算，

and, analogously, the log-space updates in equation (21) are simply multiplied by $\frac{{\tau }_a}{{\tau }_a+\text{ε}}$ and $\frac{{\tau }_b}{{\tau }_b+\text{ε}}$, respectively.
类似地，方程 ( 21 ) 中的对数空间更新分别简单地乘以 $\frac{{\tau }_a}{{\tau }_a+\text{ε}}$ 和 $\frac{{\tau }_b}{{\tau }_b+\text{ε}}$ 。

Example 2: integrating multimodal data
示例 2：整合多模态数据

The increasing emergence of different omic technologies allows researchers to integrate different types of data sources to gain a more comprehensive understanding of cellular processes. These data sources can include, for example, gene expression profiles, DNA methylation profiles, protein–protein interaction data or spatial information at the single-cell level. For instance, consider a study that aims to integrate gene expression profiles X with epigenetic profiles (such as DNA methylation) Y to explore the relationship between gene regulation and epigenetics. Here, each modality lies in a different space $\mathcal{X}$ and $\mathcal{Y}$, for example, we are provided with gene expression data $x_1,\dots ,x_n\in \mathcal{X}$ and epigenetic data $y_1,\dots ,y_m\in \mathcal{Y}$, and an alignment between measurements of different data modalities, in that heterogeneous or incomparable spaces, is required. OT can be used to align the distributions of gene expression levels and DNA methylation patterns across multiple cell types or conditions. This alignment allows for a systematic comparison and identification of genes that show coordinated changes in expression and DNA methylation, shedding light on the regulatory mechanisms underlying cellular processes.
不同组学技术的不断涌现使研究人员能够整合不同类型的数据源，以更全面地了解细胞过程。这些数据源可以包括例如基因表达谱、DNA 甲基化谱、蛋白质 - 蛋白质相互作用数据或单细胞水平的空间信息。例如，考虑一项旨在整合基因表达谱 X 与表观遗传谱（如 DNA 甲基化） Y 以探索基因调控和表观遗传学之间关系的研究。在这里，每种模态位于不同的空间 $\mathcal{X}$ 和 $\mathcal{Y}$ ，例如，我们提供基因表达数据 $x_1,\dots ,x_n\in \mathcal{X}$ 和表观遗传数据 $y_1,\dots ,y_m\in \mathcal{Y}$ ，并且需要在异构或不可比的空间中对不同数据模态的测量进行对齐。OT 可用于对齐多种细胞类型或条件下的基因表达水平和 DNA 甲基化模式的分布。这种比对可以系统地比较和识别表现出表达和 DNA 甲基化协调变化的基因，从而揭示细胞过程背后的调控机制。

Multimodal alignments  多模态比对

In all the descriptions of transport given so far, we have relied on the knowledge of a cost function that can quantify the difference between two observations living in ${\mathbb{R}}^d$. Yet, in many applications, practitioners may wish to align or match data across heterogeneous measurement spaces $\mathcal{X}$ and $\mathcal{Y}$, as demonstrated by Example 2. These settings arise, for example, when integrating several modalities (Fig. 1d) or when spatially reconstructing tissues from (partially) non-spatially resolved data (Example 3, Fig. 1c). When operating across different measurement technologies or data spaces, no obvious cost for such heterogeneous observations $c:\mathcal{X}\times \mathcal{Y}\to \mathbb{R}$ is known a priori. We thus need to design a new cost objective function for couplings P that can still be used, assuming we have at least two meaningful cost functions $c_{\mathcal{X}}:{\mathcal{X}}^2\to \mathbb{R}$ and $c_{\mathcal{Y}}:{\mathcal{Y}}^2\to \mathbb{R}$ for each data space. The inspiration for this approach lies in the quadratic assignment problem, which now seeks isometric matchings, such that if the mass of a point x_i is mostly transported to y_j (P_ij) and similarly from $x_{i^{\mathrm{\prime }}}$ to $y_{j^{\mathrm{\prime }}}$ ($P_{i^{\mathrm{\prime }}{j}^{\mathrm{\prime }}}$), then the gap between costs $c_1(x_i,x_{i^{\mathrm{\prime }}})$ and $c_{\mathcal{Y}}(y_j,y_{j^{\mathrm{\prime }}})$ is small (Fig. 3a). Thus, we are aligning two data modalities based on matching the overall sample structure or geometry of the measurements. This principle (Fig. 3a) translates into the following cost⁶⁵:
到目前为止，在对传输的所有描述中，我们都依赖于成本函数的知识，该函数可以量化位于 ${\mathbb{R}}^d$ 中的两个观测值之间的差异。然而，在许多应用中，从业者可能希望跨异构测量空间 $\mathcal{X}$ 和 $\mathcal{Y}$ 对齐或匹配数据，如示例 2 所示。例如，在整合几种模态（图 1d ）或从（部分）非空间分辨数据空间重建组织（示例 3，图 1c ）时，就会出现这些设置。当跨不同的测量技术或数据空间操作时，对于这种异构观测值 $c:\mathcal{X}\times \mathcal{Y}\to \mathbb{R}$ 没有明显的成本是先验已知的。因此，我们需要为耦合 P 设计一个仍然可以使用的新成本目标函数，假设每个数据空间至少有两个有意义的成本函数 $c_{\mathcal{X}}:{\mathcal{X}}^2\to \mathbb{R}$ 和 $c_{\mathcal{Y}}:{\mathcal{Y}}^2\to \mathbb{R}$ 。这种方法的灵感来自于二次分配问题，该问题现在寻求等距匹配，使得如果点 x 的质量大部分传输到 y （ P _{i j} ），并且类似地从 $x_{i^{\mathrm{\prime }}}$ 传输到 $y_{j^{\mathrm{\prime }}}$ （ $P_{i^{\mathrm{\prime }}{j}^{\mathrm{\prime }}}$ ），则成本 $c_1(x_i,x_{i^{\mathrm{\prime }}})$ 和 $c_{\mathcal{Y}}(y_j,y_{j^{\mathrm{\prime }}})$ 之间的差距很小（图 3a ）。因此，我们根据匹配整体样本结构或测量的几何形状来对齐两种数据模态。该原理（图 3a ）转化为以下成本 ⁶⁵ ：

and the resulting optimization problem that identifies the optimal P given objective (12) is also known as Gromov–Wasserstein. Although it may seem that evaluating this cost may have a prohibitive O(n²m²) complexity owing to this quadruple sum, the properties of P ensure that this is O(nm(n + m)) in all cases⁶⁶, and even a far more favourable $O(nm({\mathrm{d}}_{\mathcal{X}}+{\mathrm{d}}_{\mathcal{Y}}))$ if both cost matrices ${[c_{\mathcal{X}}(x_i,x_{i^{\mathrm{\prime }}})]}_{i,i^{\mathrm{\prime }}}$ and ${[c_{\mathcal{Y}}(y_j,y_{j^{\mathrm{\prime }}})]}_{j,j^{\mathrm{\prime }}}$ have rank ${\mathrm{d}}_{\mathcal{X}}$ and ${\mathrm{d}}_{\mathcal{Y}}$, respectively⁶⁷. This quadratic regime can be paired with the Sinkhorn algorithm to yield efficient solvers that are guaranteed to converge to a local optimum. Note that the low-rank approach in ref. ⁶⁷ goes one step further and results in an overall linear $O(r(n+m)({\mathrm{d}}_{\mathcal{X}}+{\mathrm{d}}_{\mathcal{Y}}))$ complexity with respect to sample size, which has served as the computational foundation for a few recent applications of Gromov–Wasserstein⁶⁸.
并由此产生的优化问题，即在给定目标 ( 12 ) 的情况下确定最优 P ， 也称为 Gromov – ^Wasserstein 。尽管由于^这个四重和，评估这个成本似乎可能具有令人望而却步的 O ( n2m2 ) 复杂度， 但 P 的属性确保在所有情况下这都是 O ( nm ( n + m )) ⁶⁶ ，并且如果成本矩阵 ${[c_{\mathcal{X}}(x_i,x_{i^{\mathrm{\prime }}})]}_{i,i^{\mathrm{\prime }}}$ 和 ${[c_{\mathcal{Y}}(y_j,y_{j^{\mathrm{\prime }}})]}_{j,j^{\mathrm{\prime }}}$ 分别具有秩 ${\mathrm{d}}_{\mathcal{X}}$ 和 ${\mathrm{d}}_{\mathcal{Y}}$ ，则甚至是更有利的 $O(nm({\mathrm{d}}_{\mathcal{X}}+{\mathrm{d}}_{\mathcal{Y}}))$ ^67。 这种二次方案可以与 Sinkhorn 算法配对，以产生保证收敛到局部最优的高效求解器。请注意，参考文献中的低秩方法。 ⁶⁷ 更进一步，得到了关于样本大小的总体线性 $O(r(n+m)({\mathrm{d}}_{\mathcal{X}}+{\mathrm{d}}_{\mathcal{Y}}))$ 复杂度，这为 Gromov–Wasserstein ⁶⁸ 的一些近期应用提供了计算基础。