如何简单易懂地理解变分推断(variational inference)?
创建时间:2016-03-25 10:10:52
最后编辑:2016-03-25 10:10:52
-------------------先给你们要的简单易懂版-----------------------
最干的干货:
首先,我们的原始目标是,需要根据已有数据推断需要的分布p;当p不容易表达,不能直接求解时,可以尝试用变分推断的方法, 即,寻找容易表达和求解的分布q,当q和p的差距很小的时候,q就可以作为p的近似分布,成为输出结果了。
在这个过程中,我们的关键点转变了,从“求分布”的推断问题,变成了“缩小距离”的优化问题。
举生活中的例子太难了,还是看图说话容易些。
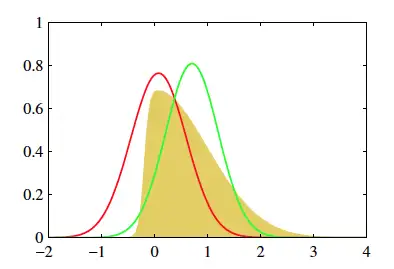
黄色的分布是我们的原始目标p,不好求。它看上去有点像高斯,那我们尝试从高斯分布中找一个红q和一个绿q,分别计算一下p和他们重叠部分面积,选更像p的q作为p的近似分布。
-----------------线性逻辑求解思路版----------------------
理解变分推断的精华步骤:
- 我们拥有两部分输入:数据x,模型p(z, x)。
- 我们需要推断的是后验概率p(z | x),但不能直接求。
- 构造后验概率p(z | x)的近似分布q(z; v)。
- 不断缩小q和p之间的距离直至收敛。
- 变分推断要解决的问题类,叫做概率机器学习问题。简单来说,专家利用他们的知识,给出合理的模型假设p(z, x),其中包括隐含变量z和观察值变量x。(需要说明的是,隐含变量z在通常情况下不止一个,并且相互之间存在依赖关系,这也是问题难求解的原因之一。)为了理解隐含变量和观察值的关系,需要说明一个很重要的概念叫做“生成过程模型”。我们认为,观察值是从已知的隐含变量组成的层次结构中生成出来的。以高斯混合模型问题举例。我们有5个相互独立的高斯分布,分别从中生成很多数据点,这些数据点混合在一起,组成了一个数据集。当我们转换角度,单从每一个数据点出发,考虑它是如何被生成的呢?生成过程分两步,第一步,从5个颜色类中选一个(比如粉红色),然后,再根据这个类对应的高斯分布,生成了这个点在空间中的位置。隐含变量有两个,第一个是5个高斯分布的参数u,第二个是每个点属于哪个高斯分布c,u和c共同组成隐含变量z。u和c之间也存在依赖关系。

2. 后验概率p(z | x)是说,基于我们现有的数据集合x,推断隐含变量的分布情况。利用高斯混合模型的例子来说,就是求得每个高斯分布的参数u的概率和每个数据点的颜色的概率c。根据贝叶斯公式,p(z | x) = p(z, x) / p(x)。 我们根据专家提供的生成模型,可知p(z, x) 部分(可以写出表达式并且方便优化),但是边缘概率p(x),是不能求得的,当z连续时,边缘概率需要对所有可能的z求积分,不好求。当z离散时,计算复杂性随着x的增加而指数增长。
3. 我们需要构造q(z; v),并且不断更新v,使得q(z;v)更接近p(z|x)。首先注意,q(z;v)的表达,意思是z是变量,v是z的概率分布q的参数。所以在构造q的时候也分两步,第一,概率分布的选择。第二,参数的选择。第一步,我们在选择q的概率分布时,通常会直观选择p可能的概率分布,这样能够更好地保证q和p的相似程度。例如高斯混合模型中,原始假设p服从高斯分布,则构造的q依然服从高斯分布。之后,我们通过改变v,使得q不断逼近p。
4. 优化问题的求解思路。优化目标很明确,减小KL散度的值即可。然而不幸的是,KL的表达式中依然有一部分不可求的后验概率。这就是为什么会有ELBO的存在原因。利用下面的等式,ELBO中只包括联合概率p(z, x)和q(z; v),从而摆脱后验概率。给定数据集后,最小化KL等价于最大化ELBO,因此ELBO的最大化过程结束时,对应获得的q(z;v*),就成为了我们的最后输出。
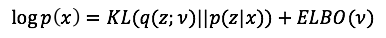
我知道,你就算背过这四步,照样不会做题,因为你尚不能达到”理解“的程度,只算”略知一二“。
----------------------追求严谨逻辑的分割线------------------------
写在前面:这部分的理解需要一些基本的概率论知识和最优化知识,适合本科生拓展阅读。你需要的是,沉下心来细细琢磨我接下来罗里吧嗦的逻辑,并且前后回顾我提到的数学符号和公式。放心,真正恶心的证明内容,在后面的后面的后面呢。
现在请你忘掉上面看到的东西,听我重头开始讲一个故事。
- Probabilistic Pipeline:
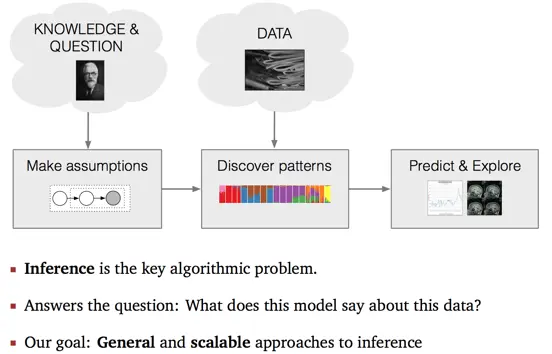
上图是概率机器学习问题的一般求解思路流程图。领域专家拥有知识可以用来建模,并且拥有问题需要被回答。他们依据拥有的知识,给出合理的假设,并且构建出数据的生成过程模型(Generative Processing Model)。模型中主要包括两部分,隐含变量,变量之间的依赖关系。利用该模型,我们希望处理获得的数据,挖掘有价值的模式,然后实现各式各样的Applications。
那么,推断的目的,就是根据我们给定的数据,可以更加细致的刻画生成过程模型中的变量吗?我个人的理解是,专家给出的假设模型相对来说泛化一些,针对不同的数据集,其中的变量的分布(参数值)会有不同,发掘的模式也自然不同。
General和Scalable是两大终极目标,我将要介绍的经典变分推断算法在一定程度上有了非常好的表现。
2. Example: Mixture of Gaussian.
高斯混合模型,作为一种生成过程模型,我们可以数学化定义如下:
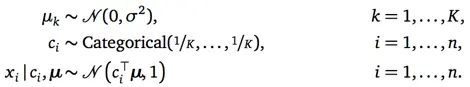
模型混合了K个相互独立的高斯分布(K是超参数),他们的方差被专家定为1(我猜这不是必须的,只是为了简化问题),他们的均值未知,但都是从一个已知的高斯分布中产生的,如第一行所示。
对任一数据点Xi,从模型中生成它的过程分两步。第一步,依据类别分布,选择Xi对应的类标签Ci,如第二行所示;第二步,从类标签Ci对应的高斯分布中产生点Xi,如第三行所示。
更细致的举例说明,如第二篇那个彩色的图,五个分布用不同颜色表示出来,代表五个类。每次从中(均匀的)选择一个类,如第三类粉红色,Ci={0,0,1,0,0} ,然后Xi的抽取依据第三个高斯分布,其均值为Ci*U=U3。自然,该点大概率出现在粉红色类覆盖的区域。
接下来的描述很关键,请别走神。
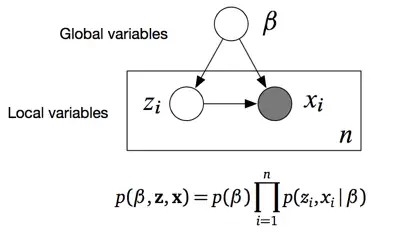
依据上述假设,专家给出的生成过程模型,包括了三个变量,其中U和C是隐含变量,Xi是观察值变量。更细致的说,U是全局变量,作用发挥在所有数据上,Ci是局部变量,只跟对应数据点Xi相关,与其他点的生成过程无关。他们之间存在的依赖关系,如盘子图所示:
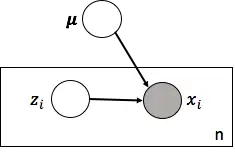
基于上述盘子图,我们可以写出表示生成模型的联合概率分布。这个联合概率就看着恶心,其实很好理解,因为,这个等式就是利用盘子图写出来的。仔细瞅,等式右边的三部分分别对应图中三个变量,独立重复的写成连乘形式,有依赖关系的写成条件概率,齐活。必须说明的是,他们三个的分布的形式,其实也是专家在一开始就已经假设好的,通常为基本分布,后续计算使用基本分布的各种特性会容易很多。
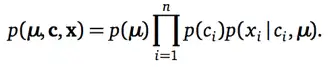
在高斯混合模型问题中,专家需要我们推断什么?事实上,我们的观测数据X,是由没有标签类的点构成的,我们需要根据这些数据集,推断C,每个点是数据哪个颜色类的,并且推断U,每个类对应的高斯分布的均值具体等于什么
3. 从形式化角度,我们到底在推测什么?推测后验概率:给定观测数据x,隐含变量的条件概率。
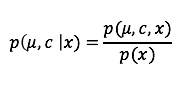
类似上述GMM的例子,我们把问题用更一般的形式表示一下,这个一般形式可以用来描述各种各样的概率机器学习模型。(如果你刚好有一个新问题想用变分推断来解决,尝试套进来)
为什么后验不好求?有了联合概率分布,求后验自然而然的想用贝叶斯公式。悲催的是,分母边缘概率intractable,如下公式所示。即使当隐含变量离散(K个值),计算的复杂度(K^n)是会随着数据量n增长呈指数增长趋势的,依然不可计算。
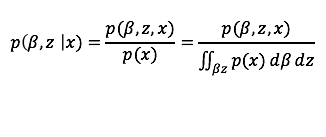
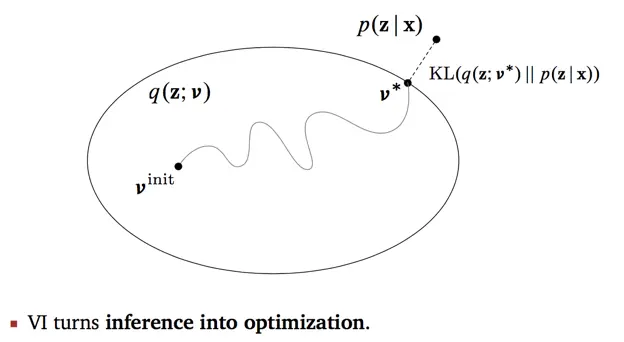
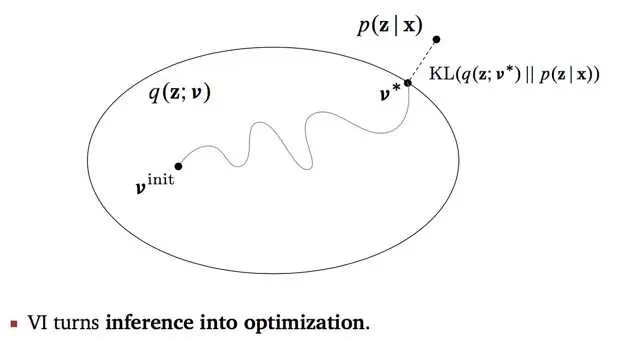
4. 首先解释这个VI主旨图。图中的大圈表示了一个distribution family,参数v是其索引,我们也可以理解为,圈是q的参数v的取值空间,每个点表示每个参数值v对应的q。用高斯混合模型的例子,我们构造q是高斯分布,但是均值参数和方差参数的值不同,代表的分布情况不同,所有的值对应的分布都是这个圈中的一个点。从V-init到V*,这条路径表示我们在迭代过程中,不断缩小的是q与p之间的距离,用KL散度衡量。
这里我觉得可以讨论一下KL。什么是KL?KL常被用来衡量两个分布的重叠程度,始终非负。当两个分布完全相同时,KL=0。为什么选KL?Blei的意思是,我们可以选其他的,不过KL makes life easy。我个人认为,针对不同的模型,可以选择其他距离函数,如果能够使得后续优化问题更方便求解。(从DNN过来的同学们请注意,我们这里是在找相似的分布,不能直接单纯用欧氏距离,去判断分布的参数值的增减导致的分布的变化)
5. 关于如何构造q(z;v)。最好的情况,我们知道p的分布是高斯,那么假设q同样是高斯分布,更可能的逼近p。其实不一定要求p是高斯分布,只要它属于exponential family,那么我们把q也放宽,q也属于这个家族即可。因为,exponential family有一个很好的性质( the Hessian of the log normalizer function a with respect to the natural parameter λ is the covariance matrix of the sufficient statistic vector t(β))这个性质允许我们很巧妙的简化了自然梯度的推导。事实上这个要求是很宽泛的,家族基本包括了我们常用的大量分布,然而不可否认的是,当p本身不属于这个家族时,q可能永远无法近似p,徘徊遥相望。这是变分推断的固有缺陷,计算结果是一个难以提前估计的近似。

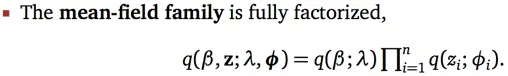
瞅瞅图,原来的分布中,非常重要的变量之间依赖关系,在构造q的时候统统打散,相互独立。它叫做mean-field,是变分推断中最基础最简单的一种构造方式(很多后续研究在用各种方法弥补丢掉的依赖信息)。
如果你有个疑问说,为什么q中没有x了。我的回答是,我们本来想求的条件概率p,是beta和z的联合分布(在给定x的情况下)。那我们的q,也是beta和z的联合分布,并且只由构造的参数决定,与x无关。
我们还是用GMM的例子形象的描述构造过程。
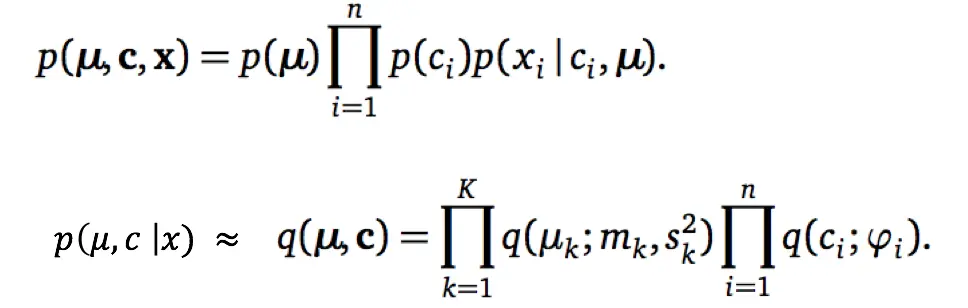
对于5个高斯分布中的某一个Uk,我们构造的q(uk;mk,sk),也属于高斯分布,因此添加了两个变分参数,m是均值,s是标准差。局部变量c_i(表示某个点属于哪一个高斯类),本属于多项式分布,因此在q中它依然是多项式分布,引入变分参数phi_i,phi_i是一个k维向量。
6.ELBO
好消息好消息,ELBO的部分其实知道个大概就可以了,不需要手动推导更新公式(推过也很快会被遗忘),可以直接尝试使用Blei组的开源项目Edword,实现自动求导求更新公式的功能。
完结。谢谢大家的赞。
更多回答
简单易懂的理解变分其实就是一句话:用简单的分布q去近似复杂的分布p。
首先,为什么要选择用变分推断?
因为,大多数情况下后验分布很难求啊。如果后验概率好求解的话我们直接EM就搞出来了。
当后验分布难于求解的时候我们就希望选择一些简单的分布来近似这些复杂的后验分布,至于这种简单的分布怎么选,有很多方法比如:Bethe自由能,平均场定理。而应用最广泛的要数平均场定理。为什么?
因为它假设各个变量之间相互独立砍断了所有变量之间的依赖关系。这又有什么好处呢?我们拿一个不太恰当的例子来形象的说明一下:用古代十字军东征来作为例子说明一下mean field。十字军组成以骑兵为主步兵为辅,开战之前骑兵手持重标枪首先冲击敌阵步兵手持刀斧跟随,一旦接战就成了单对单的决斗。那么在每个人的战斗力基本相似的情况下某个人的战斗力可以由其他人的均值代替这是平均场的思想。这样在整个军队没有什么战术配合的情况下军队的战斗力可以由这些单兵的战斗力来近似这是变分的思想。
当求解Inference问题的时候相当于积分掉无关变量求边际分布,如果变量维度过高,积分就会变得非常困难,而且你积分的分布p又可能非常复杂因此就彻底将这条路堵死了。采用平均场就是将这种复杂的多元积分变成简单的多个一元积分,而且我们选择的q是指数族内的分布,更易于积分求解。如果变量间的依赖关系很强怎么办?那就是structured mean field解决的问题了。
说到这里我们就知道了为什么要用变分,那么怎么用?
过程很简单,推导很复杂。
整个过程只需要:
1、根据图模型写出联合分布
2、写出mean filed 的形式(给出变分参数及其生成隐变量的分布)
3、写出ELBO(为什么是ELBO?优化它跟优化KL divergence等价,KL divergence因为含有后验分布不好优化)
4、求偏导进行变分参数学习
这样就搞定了!
要点都有了,具体怎么推怎么理解还得多看亲自推一遍。
把优质回答整理了一下
我们经常利用贝叶斯公式求posterior distribution P(Z |X)
P(Z | X)=\frac{p(X, Z)}{\int_{z} p(X, Z=z) d z} \\
但posterior distribution P(Z | X)求解用贝叶斯的方法是比较困难的,因为我们需要去计算\int_{z} p(X=x, Z=z) d z,而Z通常会是一个高维的随机变量,这个积分计算起来就非常困难。在贝叶斯统计中,所有的对于未知量的推断(inference)问题可以看做是对后验概率(posterior)的计算。因此提出了Variational Inference来计算posterior distribution。
那Variational Inference怎么做的呢?其核心思想主要包括两步:
- 假设一个分布q(z ; \lambda) (这个分布是我们搞得定的,搞不定的就没意义了)
- 通过改变分布的参数\lambda,使q(z ; \lambda) 靠近 p(z|x)。
总结称一句话就是,为真实的后验分布引入了一个参数化的模型。 即:用一个简单的分布q(z ; \lambda) 拟合复杂的分布p(z|x)。
这种策略将计算 p(z|x) 的问题转化成优化问题了
\lambda^{*}=\arg \min _{\lambda} \operatorname{divergence}(p(z | x), q(z ; \lambda)) \\
收敛后,就可以用 q(z;\lambda) 来代替 p(z|x)了。
KL散度
而用一个分布去拟合另一个分布通常需要衡量这两个分布之间的相似性,通常采用KL散度,当然还有其他的一些方法,像JS散度这种。下面介绍KL散度:
机器学习中比较重要的一个概念—相对熵(relative entropy)。相对熵又被称为KL散度(Kullback–Leibler divergence) 或信息散度 (information divergence),是两个概率分布间差异的非对称性度量 。在信息论中,相对熵等价于两个概率分布的信息熵的差值,若其中一个概率分布为真实分布,另一个为理论(拟合)分布,则此时相对熵等于交叉熵与真实分布的信息熵之差,表示使用理论分布拟合真实分布时产生的信息损耗 。其公式如下:
D_{K L}(p \| q)=\sum_{i=1}^{N}\left[p\left(x_{i}\right) \log p\left(x_{i}\right)-p\left(x_{i}\right) \log q\left(x_{i}\right)\right] \\
合并之后表示为:
D_{K L}(p \| q)=\sum_{i=1}^{N} p\left(x_{i}\right) \log \left(\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\right) \\
假设理论拟合出来的事件概率分布q(x)跟真实的分布p(x)一模一样,即p(x)=q(x),那么p\left(x_{i}\right) \log q\left(x_{i}\right)就等于真实事件的信息熵,这一点显而易见。在理论拟合出来的事件概率分布跟真实的一模一样的时候,相对熵等于0。而拟合出来不太一样的时候,相对熵大于0。其证明如下:
\sum_{i=1}^{N} p\left(x_{i}\right) \log \frac{q\left(x_{i}\right)}{p\left(x_{i}\right)} \leq \sum_{i=1}^{N} p\left(x_{i}\right)\left(\frac{q\left(x_{i}\right)}{p\left(x_{i}\right)}-1\right)=\sum_{i=1}^{N}\left[p\left(x_{i}\right)-q\left(x_{i}\right)\right]=0 \\
其中第一个不等式是由ln(x) \leq x -1推导出来的,只在p(x_{i})=q(x_{i})时取到等号。
这个性质很关键,因为它正是深度学习梯度下降法需要的特性。假设神经网络拟合完美了,那么它就不再梯度下降,而拟合若不完美,则会因为它大于0而继续下降。
但它有不好的地方,就是它是不对称的。也就是用P 来拟合Q 和用Q 来拟合 P 的相对熵居然不一样,而他们的距离是一样的。这也就是说,相对熵的大小并不与距离有一一对应的关系。
求解
上文引入了KL散度,但是我们本文的目的还是来求这个变分推理,不要走偏了。下面涉及一些公式等价转换:
\begin{aligned} \log P(x) &=\log P(x, z)-\log P(z | x) \\ &=\log \frac{P(x, z)}{Q(z ; \lambda)}-\log \frac{P(z | x)}{Q(z ; \lambda)} \end{aligned}\\
等式两边同时对Q(z)求期望,得:
\begin{aligned} \mathbb{E}_{q(z ; \lambda)} \log P(x) &=\mathbb{E}_{q(z ; \lambda)} \log P(x, z)-\mathbb{E}_{q(z ; \lambda)} \log P(z | x) \\ \log P(x) &=\mathbb{E}_{q(z ; \lambda)} \log \frac{p(x, z)}{q(z ; \lambda)}-\mathbb{E}_{q(z ; \lambda)} \log \frac{p(z | x)}{q(z ; \lambda)} \\ &=K L(q(z ; \lambda) \| p(z | x))+\mathbb{E}_{q(z ; \lambda)} \log \frac{p(x, z)}{q(z ; \lambda)} \\ \log P(x) &=K L(q(z ; \lambda) \| p(z | x))+\mathbb{E}_{q(z ; \lambda)} \log \frac{p(x, z)}{q(z ; \lambda)} \end{aligned}\\
到这里我们需要回顾一下我们的问题,我们的目标是使 q(z;\lambda) 靠近 p(z|x) ,就是求解:
\min_\lambda KL(q(z;\lambda)||p(z|x)) \\
而由于 KL(q(z;\lambda)||p(z|x))中包含 p(z|x),这项非常难求。借助上述公示的推导变形得到的结论:
\log P(x) =K L(q(z ; \lambda) \| p(z | x))+\mathbb{E}_{q(z ; \lambda)} \log \frac{p(x, z)}{q(z ; \lambda)} \\
将\lambda看做变量时,\text{log}P(x) 为常量,所以, \min_\lambda KL(q(z;\lambda)||p(z|x))等价于 :
\max_\lambda \mathbb E_{q(z;\lambda)}\text{log}\frac{p(x,z)}{q(z;\lambda)} \\
现在,variational inference的目标变成:
\max_{\lambda}\mathbb E_{q(z;\lambda)}[\text{log}p(x,z)-\text{log}q(z;\lambda)] \\
\mathbb E_{q(z;\lambda)}[\text{log}p(x,z)-\text{log}q(z;\lambda)]称为Evidence Lower Bound(ELBO)。p(x)一般被称之为evidence,又因为 KL(q||p)>=0, 所以 p(x)>=E_{q(z;\lambda)}[\text{log}p(x,z)-\text{log}q(z;\lambda)], 这就是为什么被称为ELBO。
ELBO
ELBO公式表达为:
\mathbb E_{q(z;\lambda)}[\text{log}p(x,z)-\text{log}q(z;\lambda)] \\
原公式可表示为:
\log P(x) =K L(q(z ; \lambda) \| p(z | x))+\mathbb{E}_{q(z ; \lambda)} \log \frac{p(x, z)}{q(z ; \lambda)} \\
引入ELBO表示为:
\log P(x) =K L(q(z ; \lambda) \| p(z | x))+ELBO \\
实际上EM算法(Expectation-Maximization)就是利用了这一特征,它分为交替进行的两步:E step假设模型参数不变,q(z)=p(z|x),计算对数似然率,在M step再做ELBO相对于模型参数的优化。与变分法比较,EM算法假设了当模型参数固定时, p(z|x) 是易计算的形式,而变分法并无这一限制,对于条件概率难于计算的情况,变分法仍然有效。
那如何来求解上述公式呢?下面介绍平均场(mean-field)、蒙特卡洛、和黑盒变分推断 (Black Box Variational Inference) 的方法。
平均场变分族(mean-field variational family)
之前我们说我们选择一族合适的近似概率分布 q(Z;\lambda),那么实际问题中,我们可以选择什么形式的 q(Z;\lambda) 呢?
一个简单而有效的变分族为平均场变分族(mean-field variational family)。它假设了隐藏变量间是相互独立的:
q(Z;\lambda) = \prod_{k=1}^{K}q_k(Z_k;\lambda_k) \\
这个假设看起来似乎比较强,但实际应用范围还是比较广泛,我们可以将其延展为将有实际相互关联的隐藏变量分组,而化为各组联合分布的乘积形式即可。
利用ELBO和平均场假设,我们就可以利用coordinate ascent variational inference(简称CAVI)方法来处理:
- 利用条件概率分布的链式法则有 :
p\left(z_{1: m}, x_{1: n}\right)=p\left(x_{1: n}\right) \prod_{j=1}^{m} p\left(z_{j} | z_{1:(j-1)}, x_{1: n}\right) \\
- 变分分布的期望为:
E\left[\log q\left(z_{1: m}\right)\right]=\sum_{j=1}^{m} E_{j}\left[\log q\left(z_{j}\right)\right] \\
将其代入ELBO的定义得到:
E L B O=\operatorname{logp}\left(x_{1: n}\right)+\sum_{j=1}^{m} E\left[\log p\left(z_{j} | z_{1:(j-1)}, x_{1: n}\right)\right]-E_{j}\left[\log q\left(z_{j}\right)\right] \\
将其对 z_{k} 求导并令导数为零有:
\frac{d E L B O}{d q\left(z_{k}\right)}=E_{-k}\left[\log p\left(z_{k} | z_{-k}, x\right)\right]-\log q\left(z_{k}\right)-1=0 \\
由此得到coordinate ascent 的更新法则为:
q^{*}\left(z_{k}\right) \propto \exp E_{-k}\left[\log p\left(z_{k}, z_{-k}, x\right)\right] \\
我们可以利用这一法则不断的固定其他的z 的坐标来更新当前的坐标对应的z值,这与Gibbs Sampling过程类似,不过Gibbs Sampling是不断的从条件概率中采样,而CAVI算法中是不断的用如下形式更新:
q^{*}\left(z_{k}\right) \propto \exp E[\log (\text {conditional})] \\
其完整算法如下所示:

MCMC
MCMC方法是利用马尔科夫链取样来近似后验概率,变分法是利用优化结果来近似后验概率,那么我们什么时候用MCMC,什么时候用变分法呢?
首先,MCMC相较于变分法计算上消耗更大,但是它可以保证取得与目标分布相同的样本,而变分法没有这个保证:它只能寻找到近似于目标分布一个密度分布,但同时变分法计算上更快,由于我们将其转化为了优化问题,所以可以利用诸如随机优化(stochastic optimization)或分布优化(distributed optimization)等方法快速的得到结果。所以当数据量较小时,我们可以用MCMC方法消耗更多的计算力但得到更精确的样本。当数据量较大时,我们用变分法处理比较合适。
另一方面,后验概率的分布形式也影响着我们的选择。比如对于有多个峰值的混合模型,MCMC可能只注重其中的一个峰而不能很好的描述其他峰值,而变分法对于此类问题即使样本量较小也可能优于MCMC方法。
黑盒变分推断(BBVI)
ELBO公式表达为:
\mathbb E_{q(z;\lambda)}[\text{log}p(x,z)-\text{log}q(z;\lambda)] \\
对用参数\theta替代\lambda,并对其求导:
\nabla_{\theta} \operatorname{ELBO}(\theta)=\nabla_{\theta} \mathbb{E}_{q}\left(\log p(x, z)-\log q_{\theta}(z)\right) \\
直接展开计算如下:
\begin{aligned} & \frac{\partial}{\partial \theta} \int q_{\theta}(z)\left(\log p(x, z)-\log q_{\theta}(z)\right) d z \\ =& \int \frac{\partial}{\partial \theta}\left[q_{\theta}(z)\left(\log p(x, z)-\log q_{\theta}(z)\right)\right] d z \\ =& \int \frac{\partial}{\partial \theta}\left(q_{\theta}(z) \log p(x, z)\right)-\frac{\partial}{\partial \theta}\left(q_{\theta}(z) \log q_{\theta}(z)\right) d z \\ =& \int \frac{\partial q_{\theta}(z)}{\partial \theta} \log p(x, z)-\frac{\partial q_{\theta}(z)}{\partial \theta} \log q_{\theta}(z)-\frac{\partial q_{\theta}(z)}{\partial \theta} d z \end{aligned}\\
由于:
\int \frac{\partial q_{\theta}(z)}{\partial \theta} d z=\frac{\partial}{\partial \theta} \int q_{\theta}(z) d z=\frac{\partial}{\partial \theta} 1=0 \\
因此:
\begin{aligned} \nabla_{\theta} \operatorname{ELBO}(\theta) &=\int \frac{\partial q_{\theta}(z)}{\partial \theta}\left(\log p(x, z)-\log q_{\theta}(z)\right) d z \\ &=\int q_{\theta}(z) \frac{\partial \log q_{\theta}(z)}{\partial \theta}\left(\log p(x, z)-\log q_{\theta}(z)\right) d z \\ &=\int q_{\theta}(z) \nabla_{\theta} \log q_{\theta}(z)\left(\log p(x, z)-\log q_{\theta}(z)\right) d z \\ &=\mathbb{E}_{q}\left[\nabla_{\theta} \log q_{\theta}(z)\left(\log p(x, z)-\log q_{\theta}(z)\right)\right] \end{aligned}\\
然后写成 SGD,就是所谓 Black Box Variational Inference (BBVI)。
\begin{aligned} & \mathbb{E}_{z \sim q_{\theta}(z)}\left[\nabla_{\theta} \log q_{\theta}(z)\left(\log p(x, z)-\log q_{\theta}(z)\right)\right] \\ \approx & \frac{1}{N} \sum_{i=1}^{N} \nabla_{\theta} \log q_{\theta}\left(z_{i}\right)\left(\log p\left(x, z_{i}\right)-\log q_{\theta}\left(z_{i}\right)\right) \end{aligned}\\
其中z_{i} \sim q_{\theta}(z)。





